평균 이동(Mean Shift)

intro

평균이동은 K-Means 알고리즘과 동일하게 군집의 중심점을 이동화며 최적의 위치를 찾는 군집화 알고리즘이다. 차이가 있다면, K-Means는 각 데이터와의 거리를 기반으로 중심점을 업데이트 한다면, 평균이동은 데이터의 밀도가 가장 높은 곳으로 중심점을 업데이트 한다.

데이터의 밀도를 파악하기 위해서 확률밀도함수를 사용하며, 모델의 확률밀도함수를 찾기 위해 KDE(Kernel Density Function)를 이용한다.(확률에 대한 공부를 깊게 하지 않아 이 말이 정확히 와닫지 않는다. 확률 공부도 예정되어있으므로 공부 후 업데이트 하겠다.)

평균이동 알고리즘 동작 원리

평균이동을 통해 최적의 중심점을 찾는 과정은 아래와 같다.
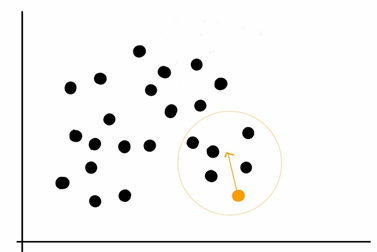1. 초기 중심점 기준으로 주변 데이터의 분포를 KDE를 사용하여 계산한다.
2. 데이터 분포가 가장 높은 지점으로 중심점을 이동한다.
3. 1번 과정과 2번 과정을 반복하여 수행하는데, 지정된 반복 횟수만큼 수행한다.

KDE는 개별 데이터에 커널 함수(예를 들면 가우시안 분포 함수)를 적용한 후 그 결과들의 평균을 내서 계산한다.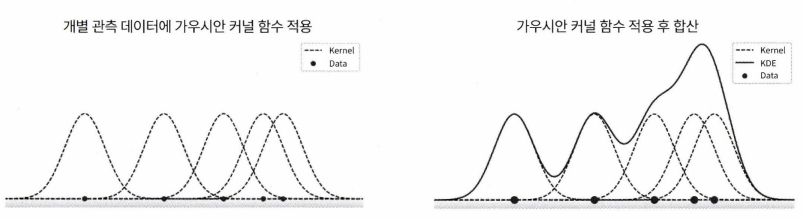그러면 오른쪽 같은 그림이 나오는데, 데이터가 몰려있는 곳이 큰 KDE 값을 가지는 것을 볼 수 있다. KDE를 계산함에 있어 가장 중요한 것은 '대역폭(bandwidth)'이다. 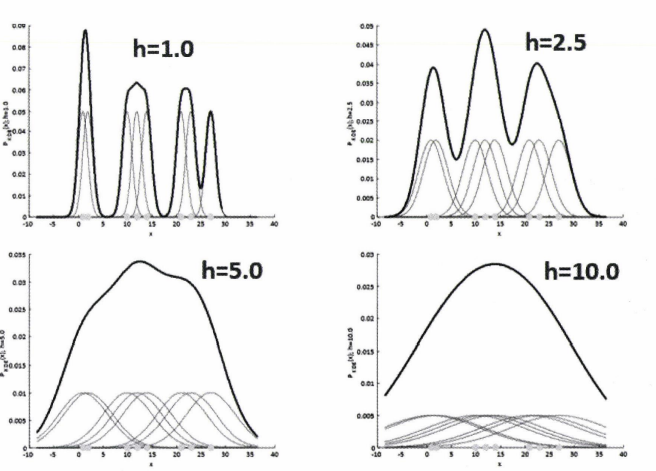KDE의 형태를 대역폭이 결정하는데, 대역폭의 크기에 따라 갖는 특성은 다음과 같다.

• 대역폭이 작을 때
  • KDE의 결과가 뾰족하다.
  • 군집의 중심점이 많다.
  • 과대적합의 위험이 있다.
• 대역폭이 클 때
  • KDE의 결과가 뭉툭하다.
  • 군집에 중심점이 적다.
  • 과소적합의 위험이 있다.

평균 이동의 사용

평균 이동 알고리즘은 sklearn.cluster 모듈에 MeanSfift 클래스에 구현되어 있다. 가장 중요한 하이퍼파라미터는 위에서 언급한 것과 같이 대역폭이다.(파라미터 이름은 badnwidth)

from sklearn.cluster import MeanShift

meanshift = MeanShift(bandwidth=1.0)
meanshift.fit(data)

K-Means와의 차이점으로는 군집의 개수는 하이퍼파라미터가 아니라는 점이다. 대역폭의 크기에 따라 군집화를 수행하기 때문이다. 그 만큼 대역폭은 평균 이동 알고리즘에서 중요한데, 최적의 대역폭을 찾을 수 있게 해주는 클래스가 있다. 바로 estimate_bandwidth 이다.

from sklearn.cluster import estimate_bandwidth

eb = estimate_bandwidth(data)

평균 이동도 중심점을 기준으로 군집을 나누는 방법이므로 cluster_centers_ 속성으로 군집의 중심점을 확인할 수 있다.