Gaussian Mixture Model

GMM 개념

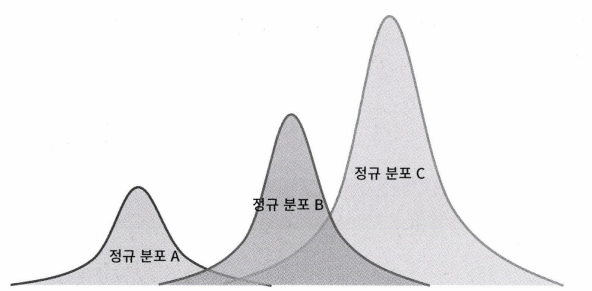
앞서 살펴본 K-means 모델은 데이터와 중심점의 거리를 계산하여 중심점을 선택하는 거리 기반 모델이었다. 이제부터 살펴볼 GMM은 확률 기반 모델이다. GMM은 군집화 하려는 데이터들이 모두 가우시안 분포를 따른다고 가정한다.(가우시안 분포 = 정규분포) 이름에서도 알 수 있듯 GMM은 군집화 대상 데이터가 여러 개의 정규분포가 하나로 합쳐진 것으로 간주한다.

GMM 사용

GMM은 sklearn.mixture 모듈 안에 GaussianMixture 클래스로 구현되어있다. K-Means와 동일하게 가장 중요한 하이퍼 파라미터는 군집의 개수이며 n_components라는 하이퍼파리미터로 군집 개수를 조절한다.

from sklearn.mixture import GaussianMixture

gm = GaussianMixture(n_components=3)
gm.fit(data)

K-means와 비교

K-Means는 앞서 설펴본 것과 같이 군집을 원형의 범위로 설정한다. 아래는 K-Means 설명 중 일부를 캡쳐한 것이다.(손으로 직접 그리느라 완벽한 원형이 아니다..ㅎㅎ)

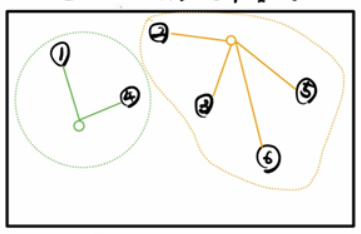
따라서 K-means는 데이터의 분포가 원형일 때 좋은 성능을 보인다. 그런데 데이터가 원형이 아닌 타원형 모양이면 어떻게 될까?

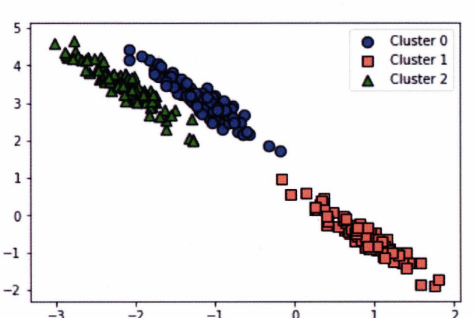
세 개의 군집으로 더미 데이터를 생성한다. 데이터는 원형이 아닌 타원형 형태로 분포해있다. 이 데이터에 K-Means를 적용하면 아래와 같은 결과가 나온다.

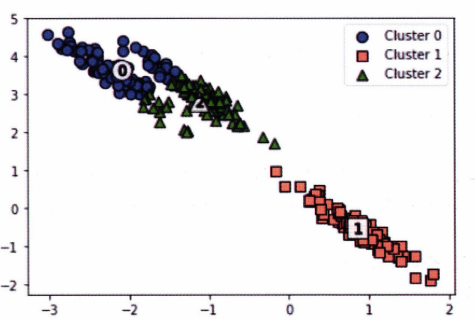
정확한 군집화가 잘 되지 않았다! 그렇다면 GMM은 어떨까?

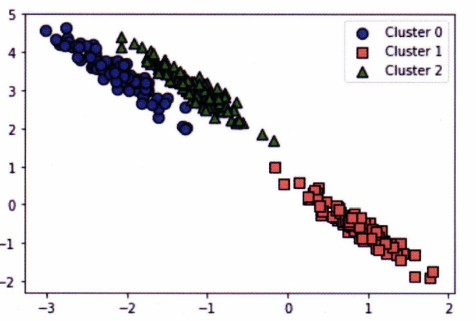
GMM은 완벽하게 군집으로 나누었다. 이처럼 GMM은 K-Means보다 데이터의 형태에 유연하게 적용이 가능하다.