벡터란?

선형대수를 이루는 모든 근간은 벡터이다. Mathematics for Machine Learning에서도 잠깐 언급한 것과 같이 행렬도 벡터의 조합이기 때문이다. 그렇다면 벡터란 무엇일까? 학문에 따라 벡터를 바라보는 시각이 조금 다르다.

• 물리학
  • 벡터를 한 공간에서의 화살표로 본다.
  • 벡터는 길이(힘)와 방향이 있으며 어떤 벡터 $\overrightarrow{v}$가 있을 때 길이와 방향을 바꾸지 않고 평행이동만 한다면, $\overrightarrow{v}$는 변함이 없다고 본다.
• 컴퓨터 공학
  • 벡터는 숫자 리스트로 본다.
  • 숫자 리스트는 벡터의 좌표로도 표현할 수 있다.
    
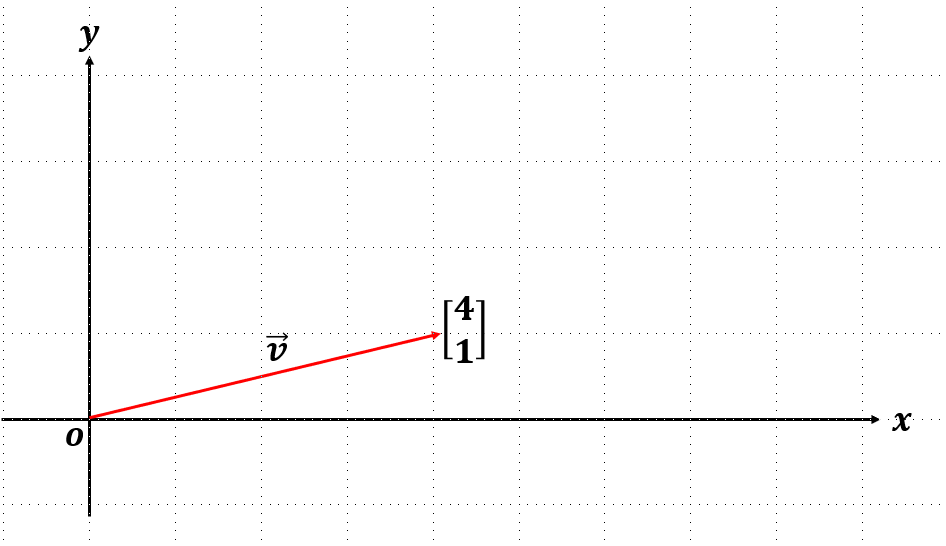
• 수학
  • 물리학 관점, 컴퓨터 공학적 관점에 더해 무엇인가 더해지거나 곱해질 수있다면 모두 벡터로 본다.
  • 따라서 벡터의 합과 곱에 대한 규칙을 찾아냈고, 선형 대수에서는 이 두 연산이 매우 중요하다!

다만, 선형대수 수업에서는 벡터를 위 그림과 같이 좌표계 안에서 원점에 시작점을 둔 화살표로 생각하자. (좌표계에서 화살표로 생각한다는 점이 물리학 관점과 같지만, 원점에 시작점을 두고 있다는 점에서 다름)

벡터의 합

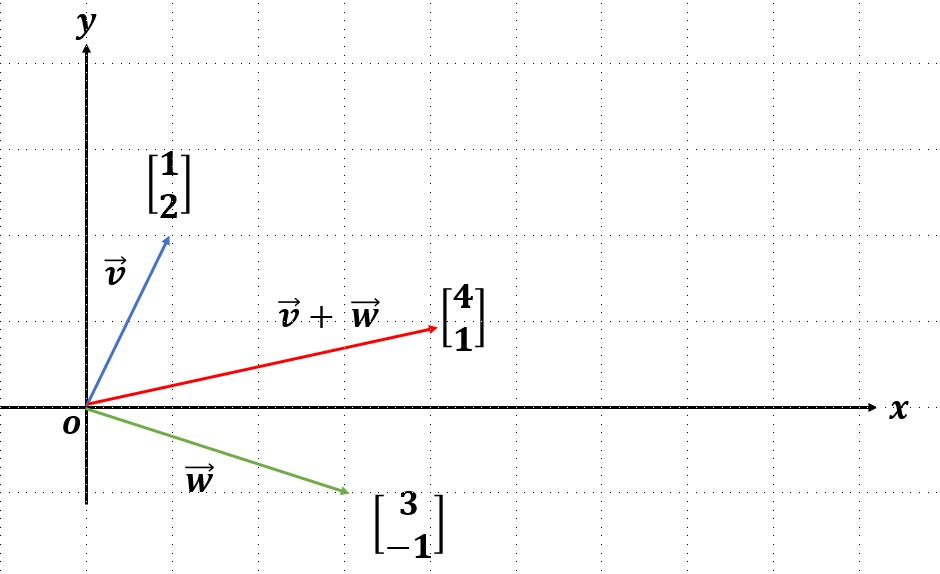벡터의 합은 위와 같이 구할 수 있다. 그런데 왜 이렇게 화살표가 가운데로 뻗고, 왜 좌표값을 축끼리 더해주는 것일까? 벡터의 합은 아래와 같은 과정을 통해 구해지기 때문이다.(벡터의 합을 구하는 과정을 처음 알게 되어 정리해본다.)

1. $\overrightarrow{w}$를 $\overrightarrow{v}$ 끝 부분으로 평행이동 한다.
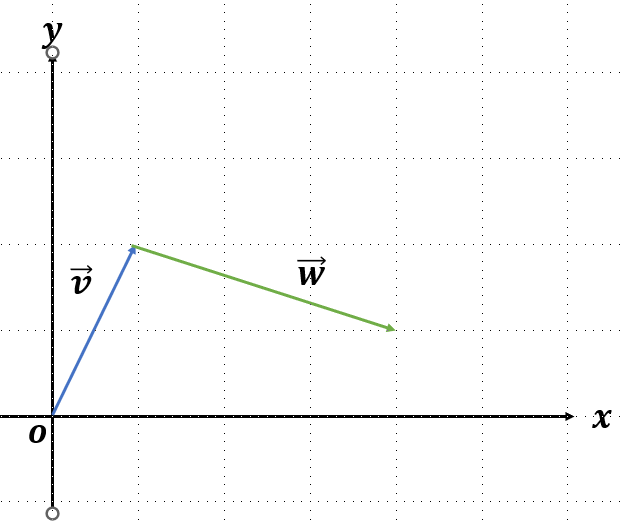   2. 원점에서 $\overrightarrow{w}$의 끝으로 화살표를 그린다.
   
   
   
   
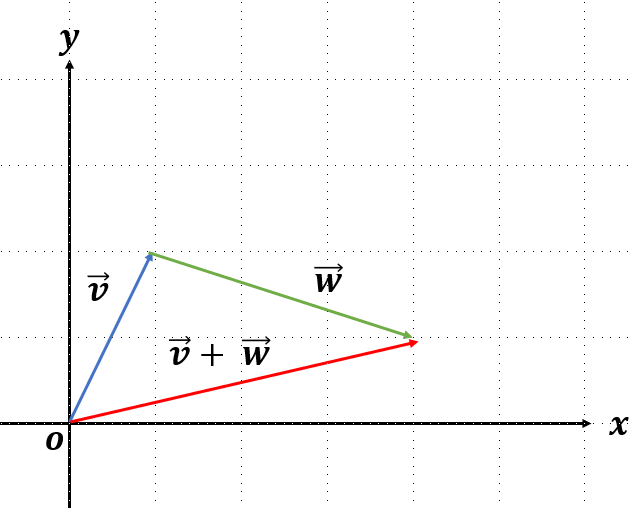
   의미적으로 보자면 아래와 같다.
   수직선에 대해 처음 배울 때, 원점에서 2를 더하고 3을 더하면 결과는 5라는 것과 같다.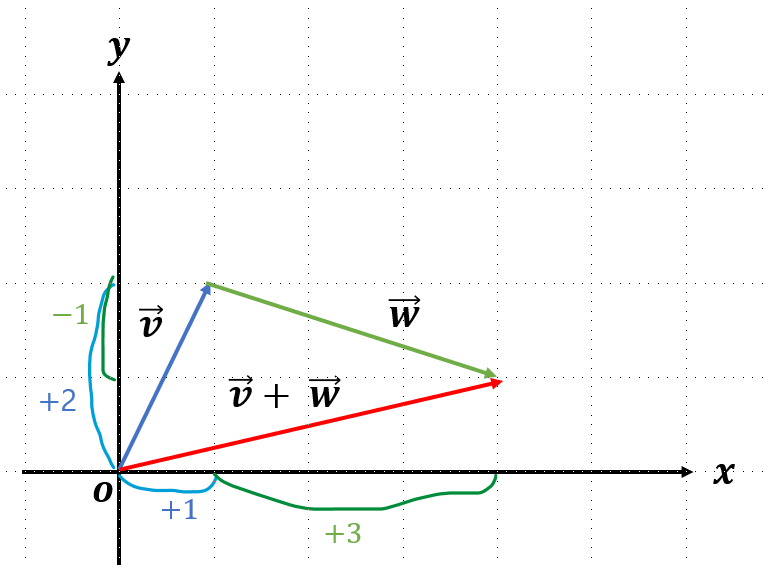

숫자만 본다면, 우리가 이미 하던 대로 각 축에 맞춰 숫자를 더해주면 된다.

벡터의 곱

벡터를 곱한다는 의미는 화살표를 늘리거나 줄이는 일을 말한다.

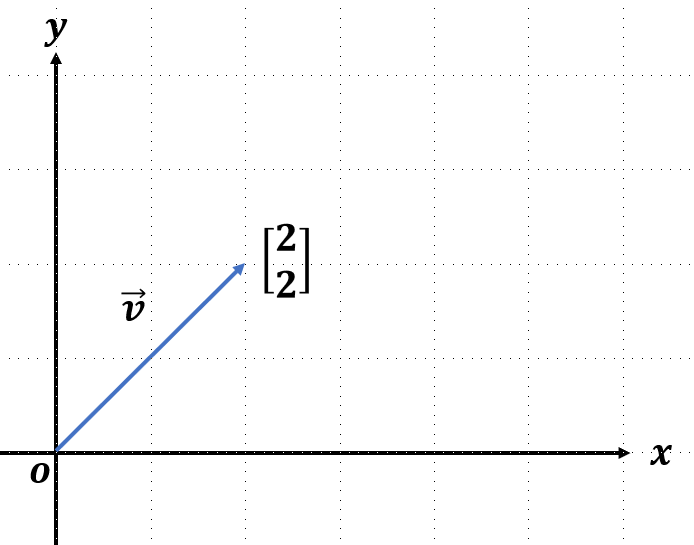
$\vec{v}$라는 원본 벡터가 있다고 할 때, $2\vec{v}$와 $-0.5\vec{v}$는 어떻게 될까?

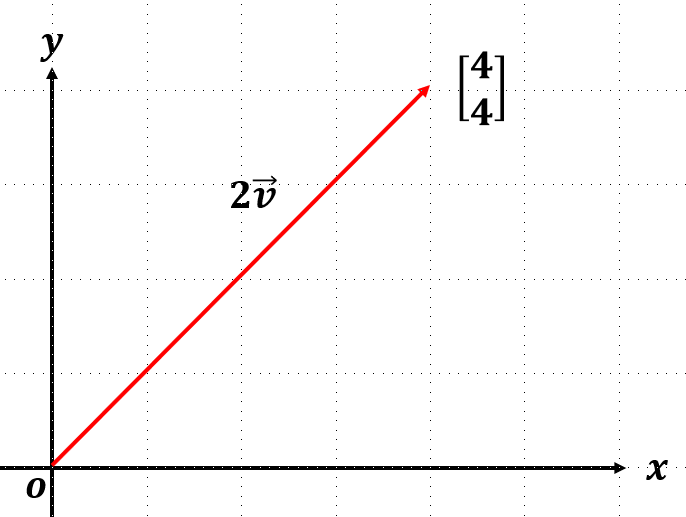
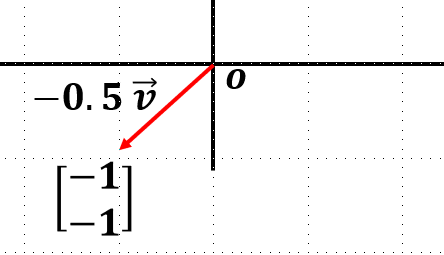곱해지는 상수만큼 길이가 길어지거나 짧아진다. 상수가 음수라면, 원점 대칭이동 시킨 후 길이를 변화한다.

벡터를 늘리거나 줄이거나 뒤집는 일을 '스케일링(scaling)'이라고 한다. 그리고 scaling을 하기 위해 곱해지는 상수를 우리는 '스칼라(scala)'라고 한다.

따라서 벡터의 스칼라만큼 모든 축에 곱해주는 것으로 이해하면되겠다.