Essence of linear algebra - Chapter 2. Linear combinations, span, and basis vectors
❗ Essence of linear algebra
기저벡터(Basis vector)
앞서 1강에서 벡터를 좌표화 하는 방법과 벡터의 기본 연산(합과 곱)에 대해 공부했다. 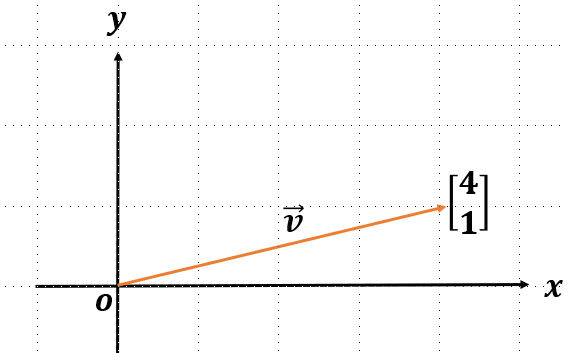 가 있다고 할때 는 로 표현할 수 있다.(한 줄에 쓰기 위해 전치행렬로 표시함) 그런데 를 각각 스칼라 4, 스칼라 1로 생각해볼 수도 있지 않을까?
가 있다고 할때 는 로 표현할 수 있다.(한 줄에 쓰기 위해 전치행렬로 표시함) 그런데 를 각각 스칼라 4, 스칼라 1로 생각해볼 수도 있지 않을까?
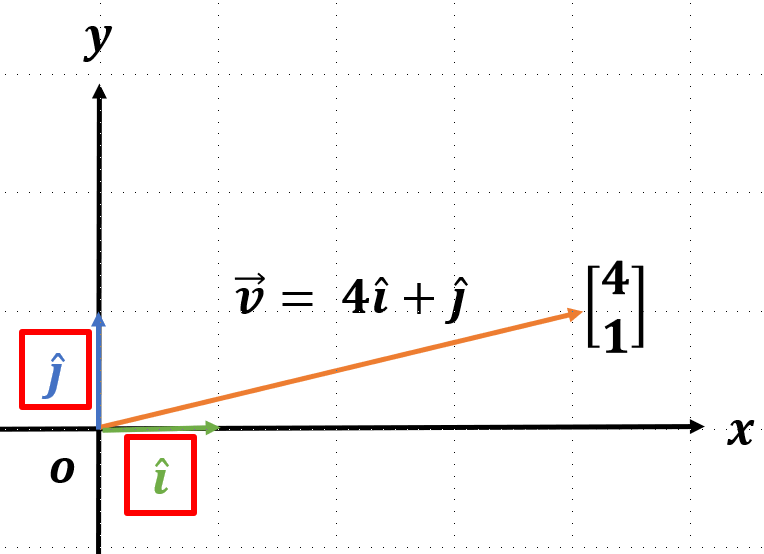 축으로 1만큼 뻗은 벡터는 , 축으로 1만큼 뻗은 벡터는 라고하고 하면 는 로 표현할 수 있다.(스케일링, 두 벡터의 합을 사용했다.) 이 때 는 축의 단위 벡터, 는 축의 단위벡터라고 표현한다.
축으로 1만큼 뻗은 벡터는 , 축으로 1만큼 뻗은 벡터는 라고하고 하면 는 로 표현할 수 있다.(스케일링, 두 벡터의 합을 사용했다.) 이 때 는 축의 단위 벡터, 는 축의 단위벡터라고 표현한다.
위에서 본 것처럼 어떤 벡터를 만들기 위한 단위 벡터를 기저벡터(basis vector)라고 한다.
※ 기저벡터는 만 있는 것이 아니고 좌표계를 나타낼 때 아무 벡터나 설정할 수 있으며, 다른 기저벡터를 사용하면 완전히 다른 좌표계가 나온다고 한다.
span - 선형조합의 결과 집합
앞서 살펴본것 처럼 두 벡터를 스케일링하고 더한 것을 선형조합(linear combination)이라고 한다.
선형조합으로 나올 수 있는 경우의 수는 3가지가 있다. 편하게 이해하기 위해 2차원을 가정한다.
-
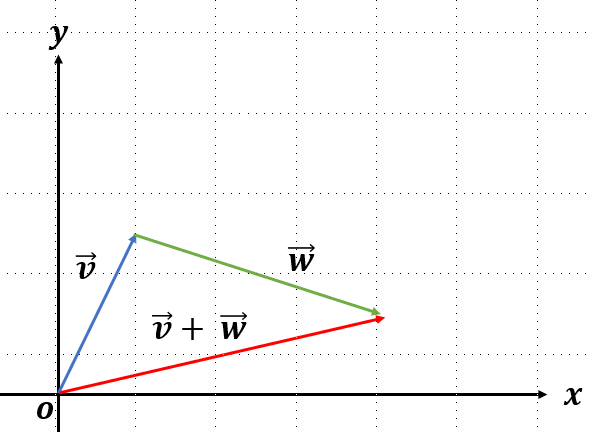
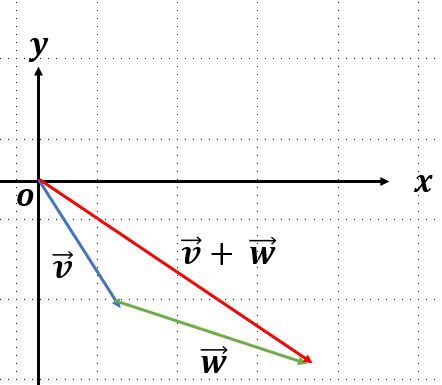
최초에 와 가 서로 다른 방향을 가르키고 있는 경우에는 좌표계의 모든 점을 표시할 수 있다. 아래에는 두 경우만을 보여주지만, 아래와 같은 방법으로 좌표 평면의 모든 벡터를 표현할 수 있다.
-
최초에 와 가 같은 방향을 가르키는 방향이 같을 때는 아무리 벡터의 합을 연산하더라도 직선을 벗어나지 못한다.
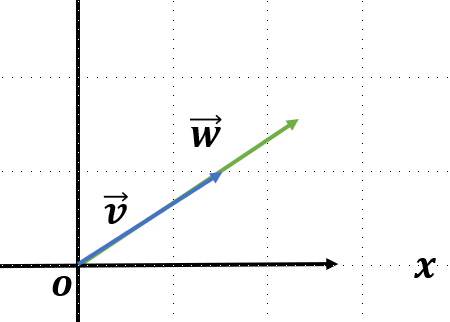
-
와 가 모두 제로 벡터일 때 원점에 갇힌다.
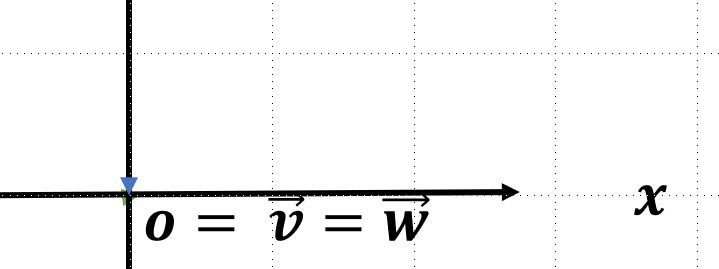
이 때 두 벡터의 선형조합으로 표현이 가능한 모든 벡터의 집합을 span이라고 한다.
스팬의 개념으로 위의 내용을 다시 말하자면
- 2차원 벡터의 span은 2차원 전체이다.
- span이 특정 선 위에 제한된다.
다시 한 번 강조하자면, 스팬은 벡터의 기본 연산인 합과 곱만을 사용해서 도달할 수 있는 벡터들의 집합이다.
Vector vs Point
스팬에 대해 생각할 때에는 벡터를 화살표가 아닌 하나의 점으로 생각하면 편하다.(화살표 끝 지점이 그 벡터의 좌표)
위에서 설명한 선형조합 예시를 점의 개념으로 다시 보면 다음과 같다.(이번에도 설명을 위해 2차원을 가정한다.)
- 2차원 span은 2차원 공간 전체이다. (모든 벡터들을 전부 표현할 수 있으므로 그 벡터들을 점으로 표현하면 2차원 공간 그 자체가 된다.)
- 2차원 공간에서 하나의 선으로 표현된다.(선형조합으로 만들어지는 벡터들이 직선을 벗어나지 못하므로 점들이 하나의 선을 이룬다.)
※ 이 부분은 시각적으로 보면 금방 이해가 되므로 강의 05:03 이후 보기
3차원에서 스팬은 어떻게 될까?
- 3차원에서 2개의 벡터를 선형조합하면 스팬은 평면 모양이다.
- 3차원에서 3개의 벡터를 선형조합하면 아래와 같은 두 경우에 따라 다르다.
- 3번째 축이 다른 두 개의 축으로 만드는 스팬(=평면) 위에 있는 경우 스팬은 변함 없이 평면이 나온다.
→ 3차원에서 2개의 벡터만 사용하면 스팬은 평면 모양이므로 - 아닌 경우에는 3차원의 모든 공간을 가르킬 수 있다.
- 3번째 축이 다른 두 개의 축으로 만드는 스팬(=평면) 위에 있는 경우 스팬은 변함 없이 평면이 나온다.
※ 이 부분은 시각적으로 보면 금방 이해가 되므로 강의 06:38 이후 보기
이것을 이해했다면, 선형 종속(linear dependent)과 선형 독립(linear independent)를 이해할 수 있다.
선형 종속은 스팬을 축소시키지 않아도 제거할 수 있는 벡터가 있는 경우를 의미한다.
예를 들어 2차원에서 두 벡터의 선형조합 결과가 하나의 선을 이룰 때 하나의 백터를 제거해도 스팬이 변하지 않는다. 또 다른 예로는 3차원에서 한 축이 나머지 두 축의 스팬 위에 있을 때, 그 한 축은 제거해도 스팬이 변하지 않는다. 이 때 선형 종속이라고 표현한다.
반대로 선형 독립은 벡터를 추가했을 때 스팬의 차원이 높아지는 경우이다.
Quiz!
다음 문장은 기저벡터와 관련된 정의이다. 왜 이 정의가 참인지 생각해보자.
The basis of a vector space is a set of linearly independent vectors that span the full space
기저벡터는 처럼 방향이 다른 벡터이며 기저벡터끼리는 선형 독립이다.(스팬에 대한 예시에서 1번 경우임) 따라서 기저벡터끼리 선형조합을 하면 스팬은 그 공간 전체가 된다.
이 질문에 대답을 하다가 다음과 같은 궁금증이 생겼다.
- 기저벡터가 왜 방향이 서로 달라야할까?
내가 이해한 기저벡터란 어떤 공간이 있을 때 그 공간을 표현할 수 있는 기준이 되는 벡터를 의미한다. 축과 축을 알면 2차원의 모든 좌표를 표현할 수 있듯이 말이다. 그런데 기저벡터의 방향이 같다면, 모든 공간을 표현할 수 없으며 기저벡터라고 말할 수 없다.(하나의 선밖에 표현할 수 없으므로)
따라서 기저벡터는 서로 방향이 달라야하며, 방향이 다르다면 선형조합으로 공간 내의 모든 지점을 전부 표시할 수 있다.