신장 트리(spanning tree)
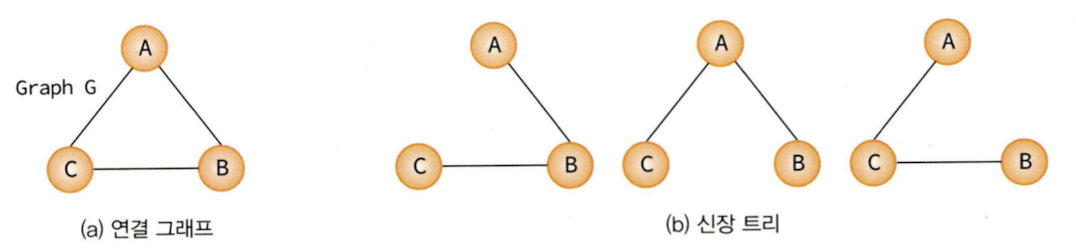
그래프 내의 모든 정점을 포함하는 트리로, 그래프의 최소 연결 부분 그래프가 된다. n개의 정점을 가지는 그래프의 신장트리는 n-1개의 간선을 가진다.
DFS와 BFS로 구한 신장 트리
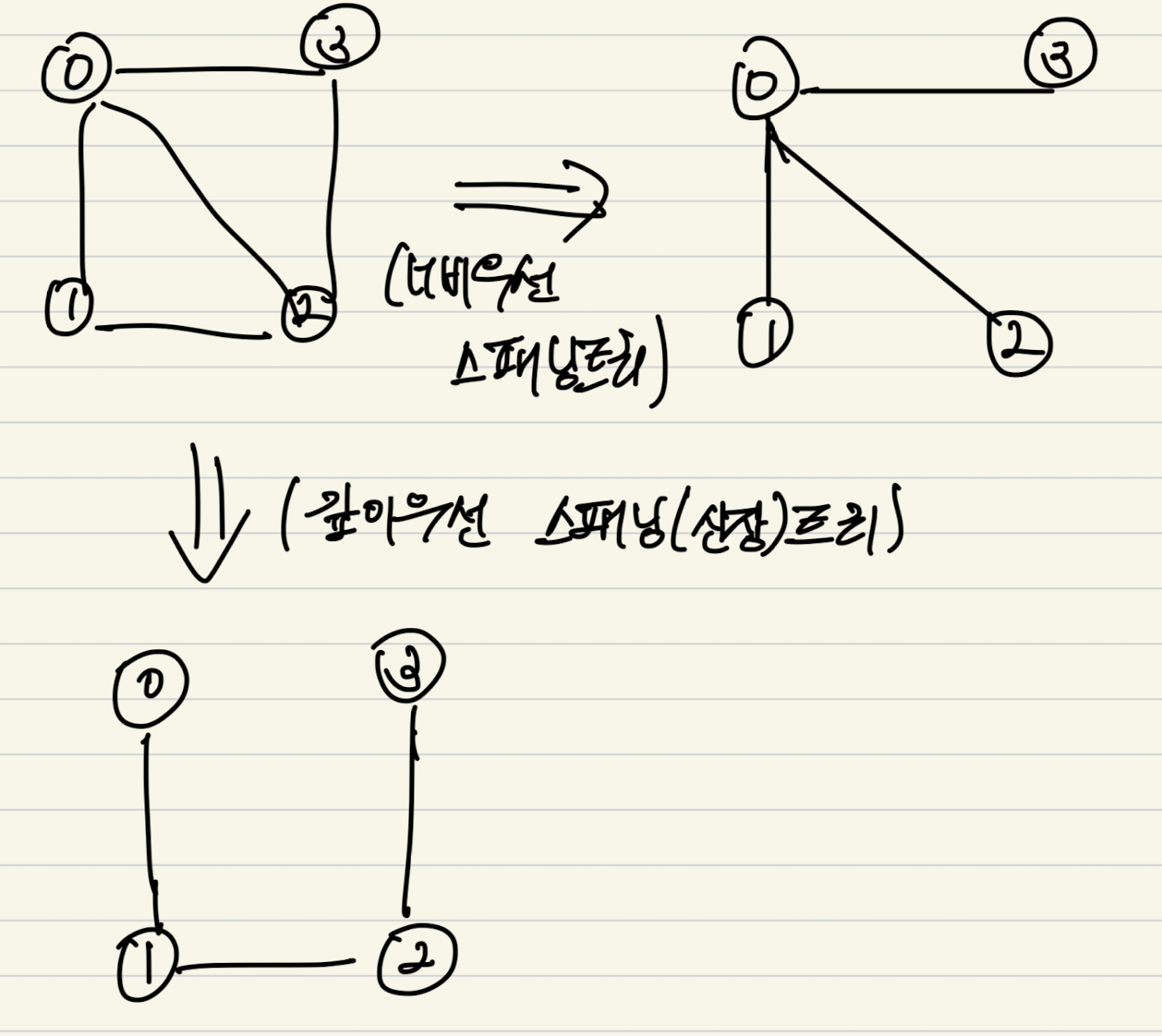
DFS와 BFS로 구한 신장 트리는 오직 하나로 유일하다.
최소 비용 신장 트리(MST: Minimum Spanning Tree)
최소 비용 신장 트리는 네트워크에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결한 것이다.
MST의 응용
최소 비용 신장 트리의 응용의 예는 다음과 같다.
- 도로 건설: 도시들은 모두 연결하면서 도로의 길이를 최소가 되도록 하는 문제
- 전기 회로: 단자들을 모두 연결하면서 전선의 길이를 가장 최소로 하는 문제
- 통신: 전화선의 길이가 최소가 되도록 전화 케이블 망을 구성하는 문제
- 배관: 파이프를 모두 연결하면서 파이프의 총 길이를 최소로 하는 문제
MST의 예
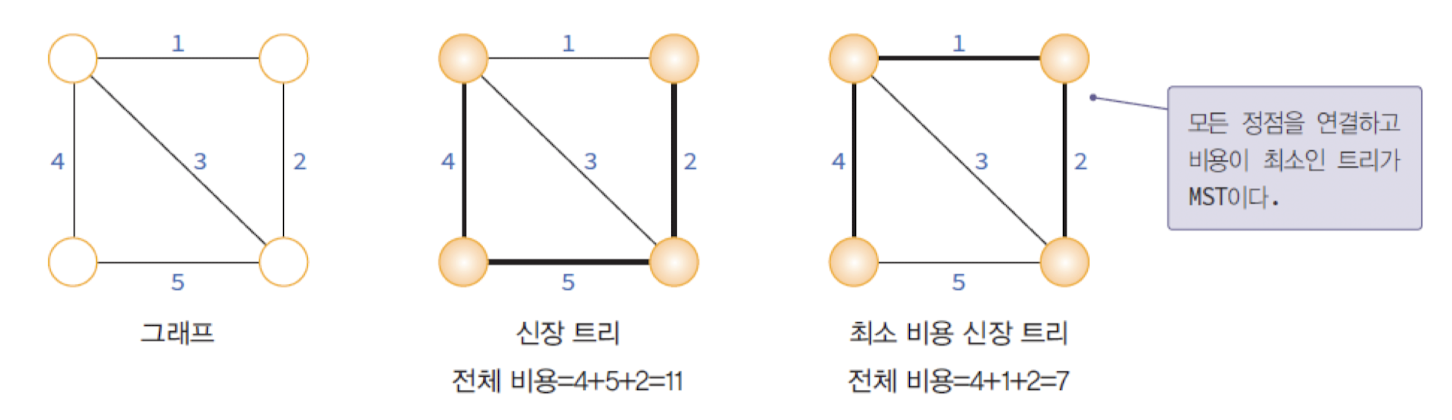
MST를 구하는 방법
MST를 구하는 방법으로는 Kruskal 알고리즘과 Prim 알고리즘이 대표적이다. 이 알고리즘들은 최소 비용 신장 트리가 간선의 가중치의 합이 최소이어야 하고, 반드시 (n-1)개의 간선만 사용해야 하며, 사이클이 포함되어서는 안 된다는 조건들을 적절히 사용하고 있다.
크루즈칼(Kruskal) 알고리즘
크루즈칼 알고리즘은 탐욕적인 방법(Greedy method)을 이용한다. 그리디는 각 단계에서 최선의 답을 선택을 반복함으로써 최종적인 해답에 도달하는 것이다. 크루즈칼 알고리즘은 그리디를 이용한 것이 최적의 해답임을 증명됐다.
크루즈칼 알고리즘 과정
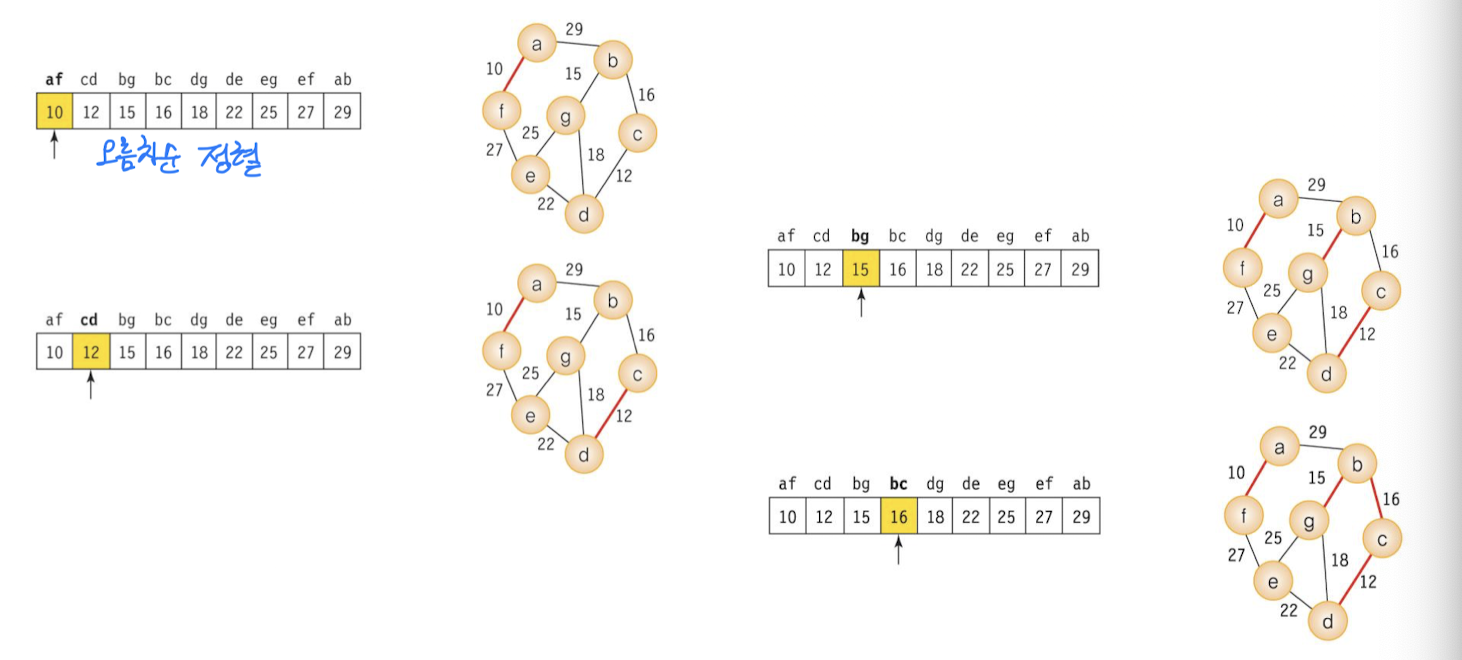
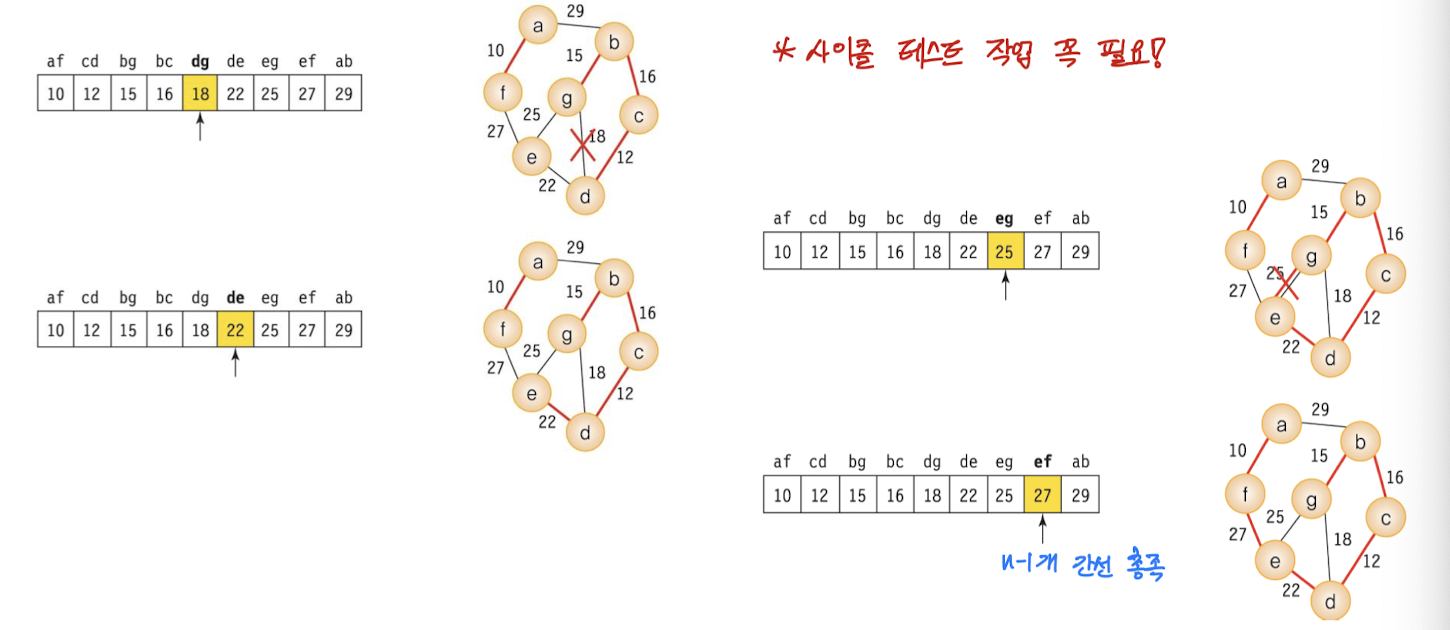
크루즈칼 알고리즘은 사이클 테스트 등의 작업은 신속하게 진행되기 때문에 대부분 간선들을 정렬하는 시간에 좌우된다.
크루즈칼 알고리즘은 사이클을 체크해야 하는데, 집합을 사용하면 간단하게 확인할 수 있다.
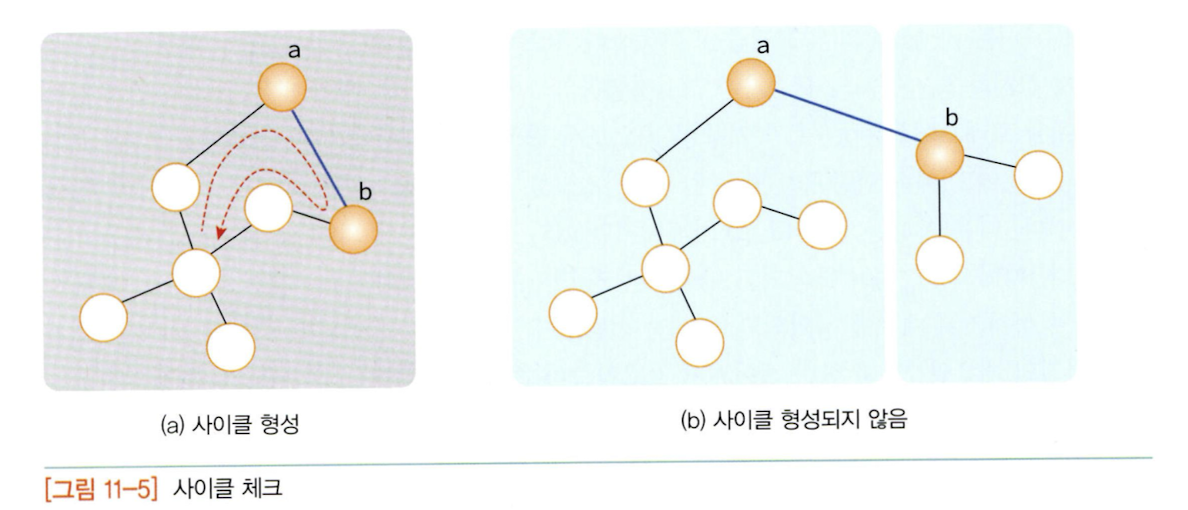
위 그림처럼 서로 다른 집합에 속하는 정점을 연결하면 사이클이 형성되지 않는다. 따라서 지금 추가하고자 하는 간선의 양끝 정점이 같은 집합에 속해 있는지를 먼저 검사해야 하는데, 이를 위한 알고리늠을 union-find 알고리즘이라 부른다.
union-find 연산
union(x, y) 연산은 원소 x와 y가 속해있는 집합을 입력ㅇ로 받아 2개의 집합의 합집합을 만든다. find(x) 연산은 원소 x가 속해있는 집합을 반환한다.
예를 들어 S={1,2,3,4,5,6}의 집합을 가정하자. 처음에는 집합의 원소를 하나씩 분리하여 독자적인 집합으로 만든다.
{1}, {2}, {3}, {4}, {5}, {6}
여기에 union(1,4)를 하면 다음과 같은 집합으로 변환한다.
{1,4}, {2}, {3}, {5}, {6}
union-find 연산의 구현
집합을 구현하는데 여러가지 방법이 있지만 가장 효율적인 방법은 트리 형태를 사용하는 것이다. 우리는 부모 노드만 알면 되므로 부모 포인터 표현을 사용한다. 부모 포인터 표현이란 각 노드에 대해 그 노드의 부모에 대한 포인터만 저장하는 것이다. 이는 두 노드가 같은 트리에 있는지를 확인하는데 효율적인 방법이다. 배열의 값이 -1인 경우 부모 노드가 없다고 판단한다.
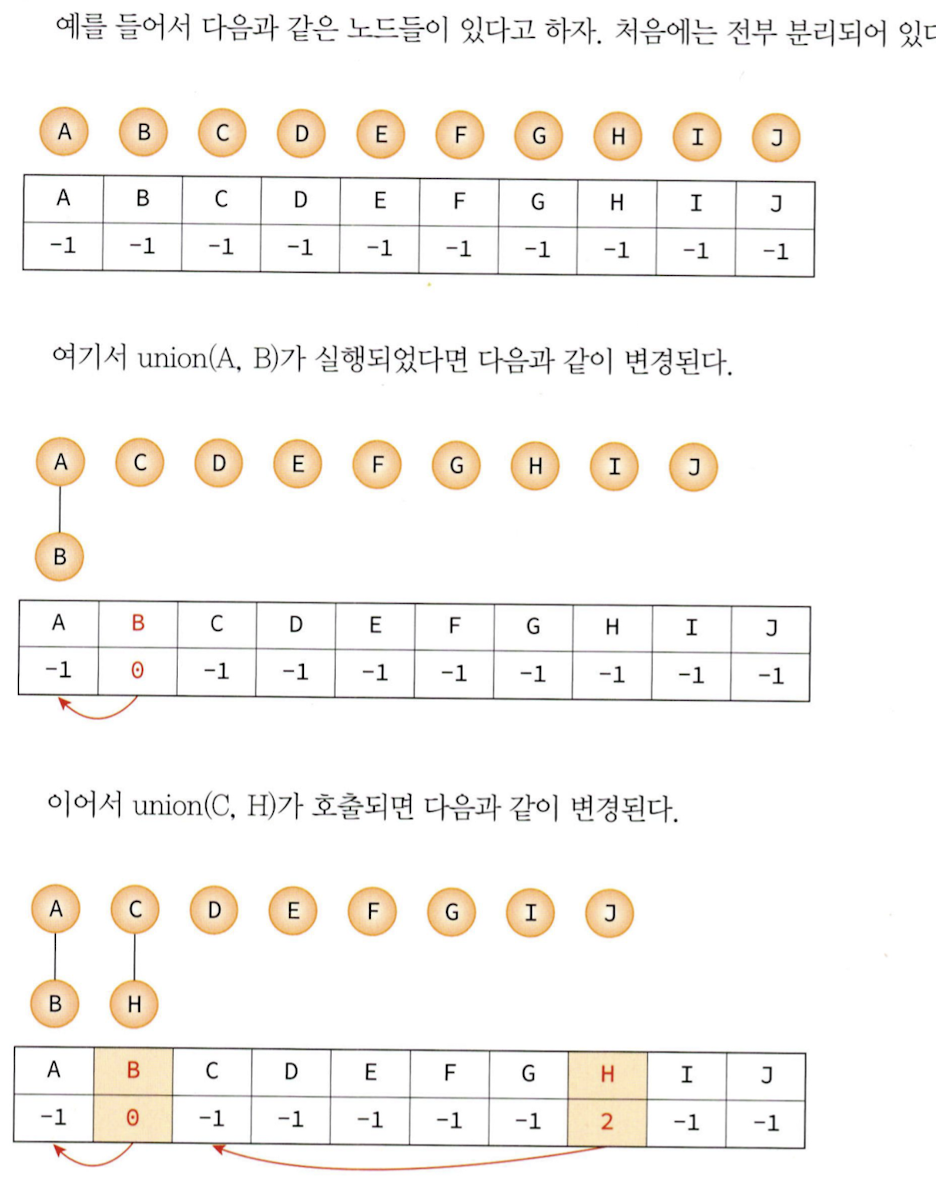
유니온 탐색을 통해 같은 루트 부모를 가리킬 경우 두 정점이 이미 같은 집합에 속해 있다고 판단한다.
크루즈칼 전체 코드
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 100
#define INF 1000
int parent[MAX_VERTICES]; // 부모 노드
// 초기화
void set_init(int n)
{
for (int i = 0; i < n; i++)
parent[i] = -1;
}
// curr가 속하는 집합을 반환한다.
int set_find(int curr)
{
if (parent[curr] == -1)
return curr; // 루트
while (parent[curr] != -1) curr = parent[curr];
return curr;
}
// 두개의 원소가 속한 집합을 합친다.
void set_union(int a, int b)
{
int root1 = set_find(a); // 노드 a의 루트를 찾는다.
int root2 = set_find(b); // 노드 b의 루트를 찾는다.
if (root1 != root2) // 부모 노드가 다르다면 서로 다른 집합
parent[root1] = root2; // 합한다.
}
struct Edge { // 간선을 나타내는 구조체
int start, end, weight;
};
typedef struct GraphType {
int n; // 간선의 개수
struct Edge edges[2 * MAX_VERTICES];
} GraphType;
// 그래프 초기화
void graph_init(GraphType* g)
{
g->n = 0;
for (int i = 0; i < 2 * MAX_VERTICES; i++) {
g->edges[i].start = 0;
g->edges[i].end = 0;
g->edges[i].weight = INF;
}
}
// 간선 삽입 연산
void insert_edge(GraphType* g, int start, int end, int w)
{
g->edges[g->n].start = start;
g->edges[g->n].end = end;
g->edges[g->n].weight = w;
g->n++;
}
// qsort()에 사용되는 함수
int compare(const void* a, const void* b)
{
struct Edge* x = (struct Edge*)a;
struct Edge* y = (struct Edge*)b;
return (x->weight - y->weight);
}
// kruskal의 최소 비용 신장 트리 프로그램
void kruskal(GraphType* g)
{
int edge_accepted = 0; // 현재까지 선택된 간선의 수
int uset, vset; // 정점 u와 정점 v의 집합 번호
struct Edge e;
set_init(g->n); // 집합 초기화
qsort(g->edges, g->n, sizeof(struct Edge), compare);
printf("크루스칼 최소 신장 트리 알고리즘 \n");
int i = 0;
while (edge_accepted < (g->n - 1)) // 간선의 수 < (n-1)
{
e = g->edges[i];
uset = set_find(e.start); // 정점 u의 집합 번호
vset = set_find(e.end); // 정점 v의 집합 번호
if (uset != vset) { // 서로 속한 집합이 다르면
printf("간선 (%d,%d) %d 선택\n", e.start, e.end, e.weight);
edge_accepted++;
set_union(uset, vset); // 두개의 집합을 합친다.
}
i++;
}
}
int main(void)
{
GraphType* g;
g = (GraphType*)malloc(sizeof(GraphType));
graph_init(g);
insert_edge(g, 0, 1, 29);
insert_edge(g, 1, 2, 16);
insert_edge(g, 2, 3, 12);
insert_edge(g, 3, 4, 22);
insert_edge(g, 4, 5, 27);
insert_edge(g, 5, 0, 10);
insert_edge(g, 6, 1, 15);
insert_edge(g, 6, 3, 18);
insert_edge(g, 6, 4, 25);
kruskal(g);
free(g);
return 0;
}크루즈칼 알고리즘의 시간복잡도
크루즈칼 알고리즘의 시간복잡도는 이다.
프림(Prim) 알고리즘
프림 알고리즘은 시작 정점에서부터 출발하여 신장 트리 집합을 단계적으로 확장해나가는 알고리즘이다. 즉, 신장 트리 집합에 인접한 정점 중에서 최저 간선으로 연결된 정점 선택하여 신장 트리 집합에 추가된다. 프림 알고리즘 역시 (n-1)개의 간선을 가진다.
프림 알고리즘 과정
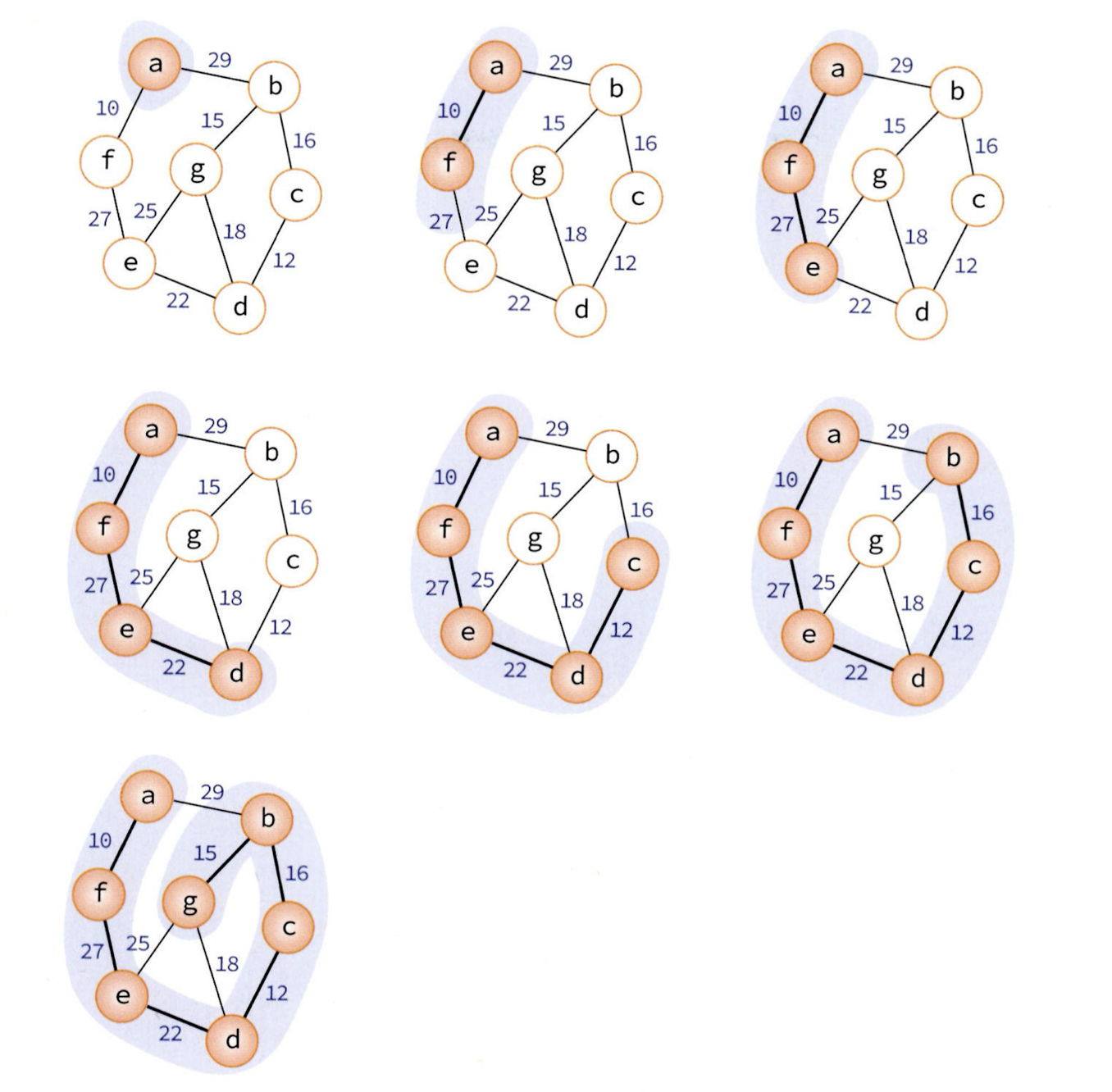
Prim 알고리즘 전체 코드
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 100
#define INF 10000
typedef struct GraphType {
int n;
int weight[MAX_VERTICES][MAX_VERTICES];
} GraphType;
int selected[MAX_VERTICES];
int distance[MAX_VERTICES];
// 최소 dist[v] 값을 갖는 정점을 반환
int get_min_vertex(int n) {
int v, i;
// 방문하지 않은 정점 찾기
for(i = 0; i < n; i++)
if (!selected[i]) {
v = i;
break;
}
// 방문하지 않고, distance 배열에서 가장 값이 작은 정점(인덱스) 반환
for (i = 0; i < n; i++)
if (!selected[i] && (distance[i] < distance[v]))
v = i;
return v;
}
void prim(GraphType* g, int s) {
int i, u, v;
for (u = 0; u < g->n; u++)
distance[u] = INF;
distance[s] = 0;
for (i = 0; i < g->n; i++) {
// 방문하지 않은 정점 중 가장 거리가 작은 정점 찾기
u = get_min_vertex(g->n);
selected[u] = TRUE;
printf("정점 %d 추가\n", u);
for (v = 0; v < g->n; v++)
if (g->weight[u][v] != INF)
if (!selected[v] && g->weight[u][v] < distance[v])
distance[v] = g->weight[u][v];
}
}
int main() {
GraphType g = { 7,
{{ 0, 29, INF, INF, INF, 10, INF },
{ 29, 0, 16, INF, INF, INF, 15 },
{ INF, 16, 0, 12, INF, INF, INF },
{ INF, INF, 12, 0, 22, INF, 18 },
{ INF, INF, INF, 22, 0, 27, 25 },
{ 10, INF, INF, INF, 27, 0, INF },
{ INF, 15, INF, 18, 25, INF, 0 } }
};
prim(&g, 0);
return 0;
}
// -- 출력 결과 --
// 정점 0 추가
// 정점 5 추가
// 정점 4 추가
// 정점 3 추가
// 정점 2 추가
// 정점 1 추가
// 정점 6 추가코드의 흐름은 다음 같다.
- get_min_vertext() 함수를 통해서 distance 배열에서 가장 작은 정점(u)를 찾는다.
- 찾은 정점 u를 방문 처리한다.
- 반복문을 통해서 현재 정점 u를 기준으로 인접한 정점을 순회하면서, 방문하지 않은 정점이고 distance 배열에 저장된 거리보다 작다면 갱신해준다.
Prim 시간 복잡도
프림 알고리즘의 시간 복잡도는 이다. 희소 그래프인 경우에는 크루즈칼 알고리즘이 유리하고, 밀집한 그래프인 경우 프림 알고리즘이 유리하다.
출처
C언어로 쉽게 풀어쓴 자료구조 - 천인구
