너비 우선 탐색(BFS: Breath first search)

BFS는 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 탐색이다.

BFS를 구현할 때는 큐(queue)를 사용하는데, 가까운 거리에 있는 정점들을 차례로 저장한 후 꺼낼 수 있는 자료구조로 큐가 적합하기 때문이다.

알고리즘을 간략히 설명해보면 큐에서 정점을 꺼내서 정점을 방문하고 인접 정점들을 큐에 추가한다. 그리고 큐가 모두 소진될 때까지 계속 이를 반복한다.

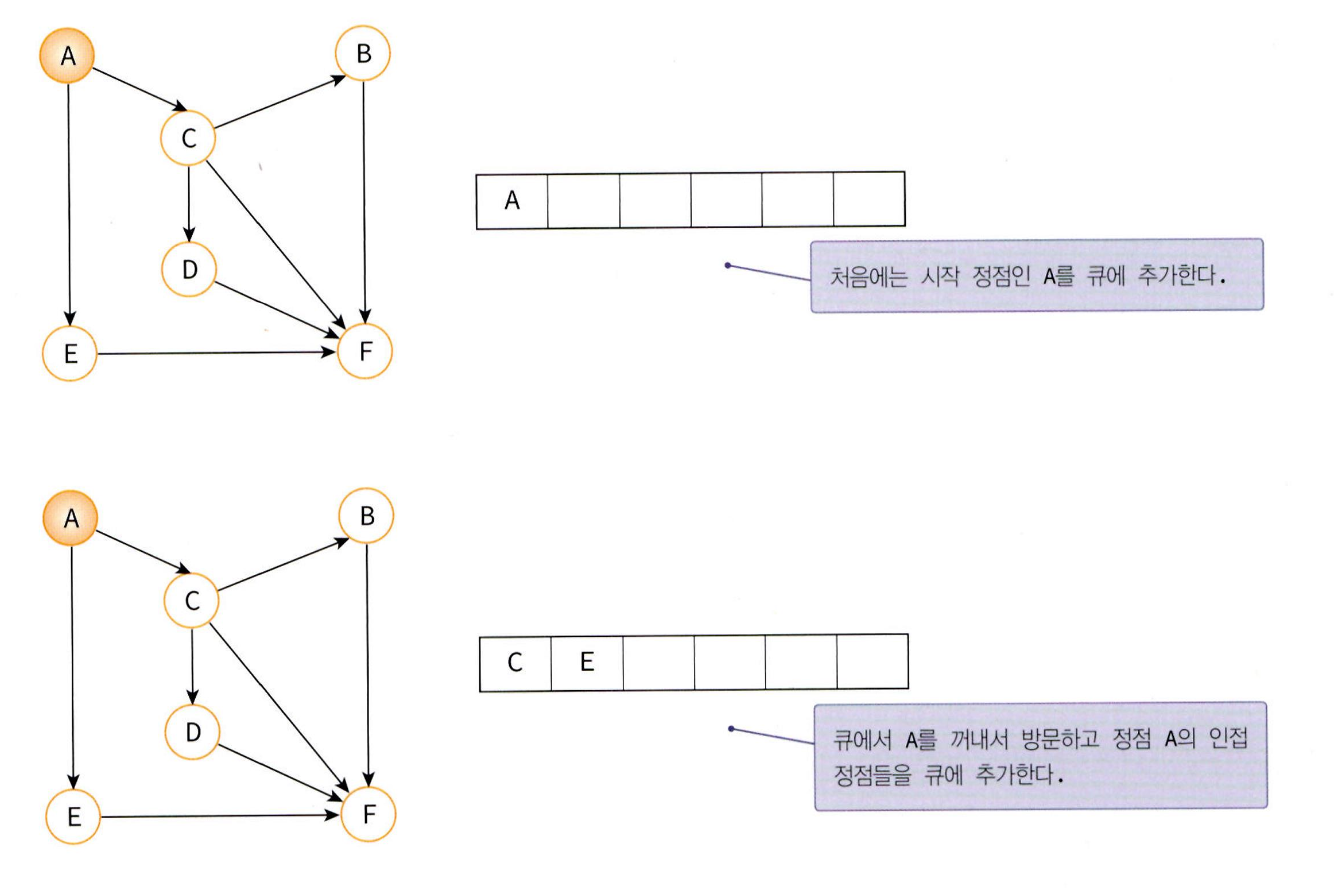
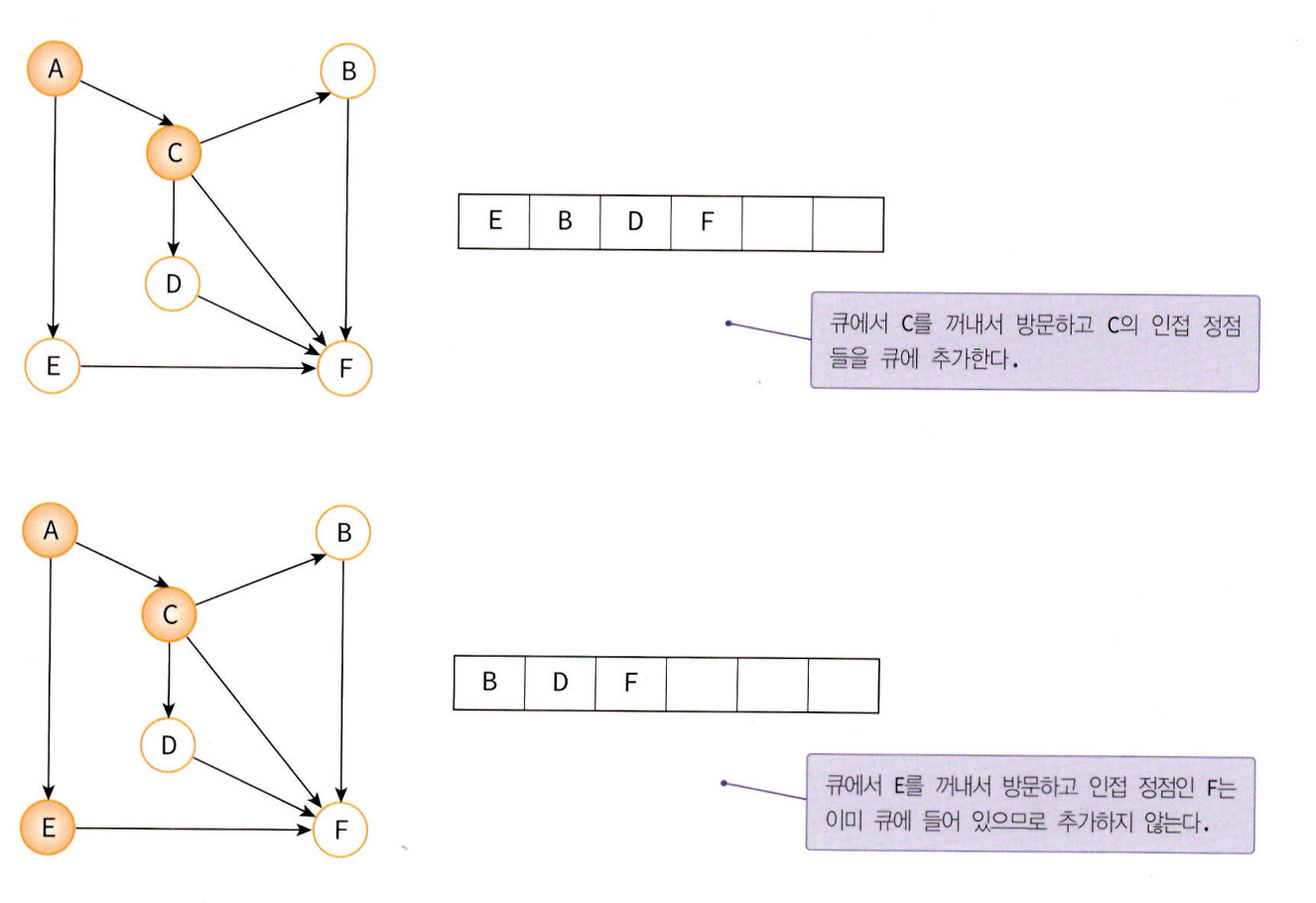
BFS 역시 DFS와 마찬가지로 인접 행렬과 인접 리스트 두 가지 방법으로 구현이 가능하다.

인접 행렬로 구현

#include <stdio.h>
#include <stdlib.h>

#define TRUE 1
#define FALSE 0
#define MAX_QUEUE_SIZE 10

typedef int element;
typedef struct { // 큐 타입
	element  queue[MAX_QUEUE_SIZE];
	int  front, rear;
} QueueType;

// 오류 함수
void error(const char* message) {
	fprintf(stderr, "%s\n", message);
	exit(1);
}

// 공백 상태 검출 함수
void queue_init(QueueType* q) {
	q->front = q->rear = 0;
}

// 공백 상태 검출 함수
int is_empty(QueueType* q) {
	return (q->front == q->rear);
}

// 포화 상태 검출 함수
int is_full(QueueType* q) {
	return ((q->rear + 1) % MAX_QUEUE_SIZE == q->front);
}

// 삽입 함수
void enqueue(QueueType* q, element item) {
	if (is_full(q))
		error("큐가 포화상태입니다");
	q->rear = (q->rear + 1) % MAX_QUEUE_SIZE;
	q->queue[q->rear] = item;
}

// 삭제 함수
element dequeue(QueueType* q) {
	if (is_empty(q))
		error("큐가 공백상태입니다");
	q->front = (q->front + 1) % MAX_QUEUE_SIZE;
	return q->queue[q->front];
}

#define MAX_VERTICES 50
typedef struct GraphType {
	int n;
	int adj_mat[MAX_VERTICES][MAX_VERTICES];
} GraphType;

int visited[MAX_VERTICES];

void graph_init(GraphType* g) {
	int r, c;
	g->n = 0;
	for (r = 0; r < MAX_VERTICES; r++)
		for (c = 0; c < MAX_VERTICES; c++)
			g->adj_mat[r][c] = 0;
}

void insert_vertex(GraphType* g, int v) {
	if (((g->n) + 1) > MAX_VERTICES) {
		error("err");
		return;
	}
	g->n++;
}

void insert_edge(GraphType* g, int start, int end) {
	g->adj_mat[start][end] = 1;
	g->adj_mat[end][start] = 1;
}

void bfs_mat(GraphType* g, int v) {
	int w;
	QueueType q;

	queue_init(&q);
	visited[v] = TRUE;
	printf("%d 방문 -> ", v);
	// 맨 처음 방문한 노드 큐에 추가
	enqueue(&q, v);
	while (!is_empty(&q)) {
		// 방문한 노드 꺼내기
		v = dequeue(&q); 
		// 방문한 노드를 기준으로 인접 노드 모두 방문
		for(w = 0; w < g->n; w++)
			// v는 현재 기준이 되는 노드
			// w는 연결된 노드
			// 즉, 아래 조건문은 v를 기준으로 연결된 노드에 방문했는지를 확인.
			if (g->adj_mat[v][w] && !visited[w]) {
				visited[w] = TRUE;
				printf("%d 방문 -> ", w);
				enqueue(&q, w);
			}
	}
}

int main() {
	GraphType* g;
	g = (GraphType*)malloc(sizeof(GraphType));
	graph_init(g);

	for (int i = 0; i < 6; i++)
		insert_vertex(g, i);

	insert_edge(g, 0, 2);
	insert_edge(g, 2, 1);
	insert_edge(g, 2, 3);
	insert_edge(g, 0, 4);
	insert_edge(g, 4, 5);
	insert_edge(g, 1, 5);
	
	printf("너비 우선 탐색\n");
	bfs_mat(g, 0);
	printf("\n");

	free(g);

	return 0;
}

인접 리스트로 구현

#define MAX_VERTICES 50
typedef struct GraphNode {
	int vertex;
	GraphNode* link;
};

typedef struct GraphType {
	int n;
	GraphNode* adj_mat[MAX_VERTICES];
} GraphType;

int visited[MAX_VERTICES];

void graph_init(GraphType* g) {
	int r, c;
	g->n = 0;
	for (r = 0; r < MAX_VERTICES; r++)
		g->adj_mat[r] = NULL;
}

void insert_vertex(GraphType* g, int v) {
	if (((g->n) + 1) > MAX_VERTICES) {
		error("err");
		return;
	}
	g->n++;
}

void insert_edge(GraphType* g, int u, int v) {
	GraphNode* node;
	node = (GraphNode*)malloc(sizeof(GraphNode));
	node->vertex = v;
	node->link = g->adj_mat[u];
	g->adj_mat[u] = node;
}

void bfs_list(GraphType* g, int v) {
	GraphNode* w;
	QueueType q;

	queue_init(&q);
	visited[v] = TRUE;
	printf("%d 방문 -> ", v);
	enqueue(&q, v);
	while (!is_empty(&q)) {
		v = dequeue(&q);
		for (w = g->adj_mat[v]; w; w = w->link) {
			if (!visited[w->vertex]) {
				visited[w->vertex] = TRUE;
				printf("%d 방문 -> ", w->vertex);
				enqueue(&q, w->vertex);
			}
		}
	}
}

int main() {
	GraphType* g;
	g = (GraphType*)malloc(sizeof(GraphType));
	graph_init(g);

	for (int i = 0; i < 6; i++)
		insert_vertex(g, i);

	insert_edge(g, 0, 2);
	insert_edge(g, 2, 1);
	insert_edge(g, 2, 3);
	insert_edge(g, 0, 4);
	insert_edge(g, 4, 5);
	insert_edge(g, 1, 5);

	printf("너비 우선 탐색\n");
	bfs_list(g, 0);
	printf("\n");

	free(g);

	return 0;
}

BFS의 시간복잡도

리스트로 구현하는 것이 더 효율적이다.

• 인접 리스트: O(n + e)
• 인접 행렬: O(n^2)

출처
C언어로 쉽게 풀어쓴 자료구조 - 천인구