최단 경로(Shortest Path)

이재원·2024년 12월 9일
다익스트라알고리즘최단경로플로이드
0

알고리즘

목록 보기
7/15

최단 경로(Shortest Path)

최단 경로 문제는 네트워크에서 정점 i와 정점 j를 연결하는 경로 중에서 간선들의 가중치 합이 최소가 되는 경로를 찾는 문제이다. 간선의 가중치는 비용, 거리, 시간 등을 나타낸다.

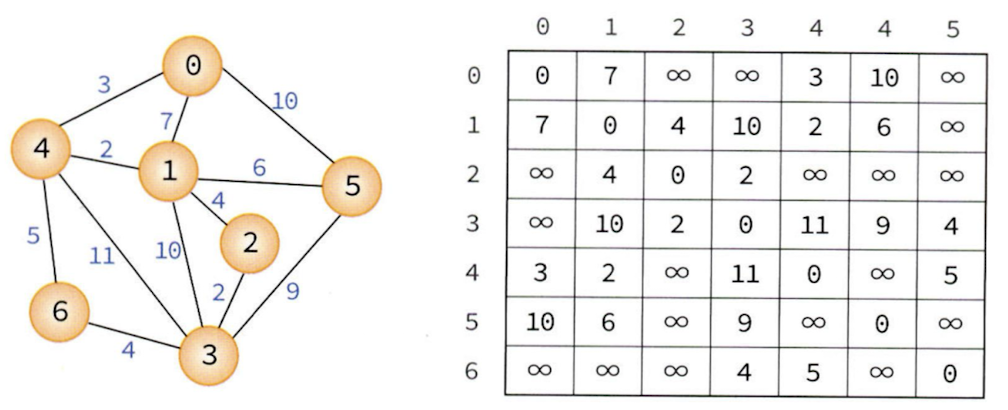
예를 들어 위 그래프에서 정점 0에서 점점 3으로 가는 최단 경로는 0,4,1,2,3 이고, 비용은 11이다. 다른 경로도 존재하지만 이 경로가 최단 거리이다. 사람은 특별한 과정 없이 바로 최단 경로를 도출할 수 있지만 이것을 어떻게 프로그램으로 만들 것인지가 관건이다.

최단 경로를 구할 수 있는 알고리즘은 Dijkstar 알고리즘과 Floyd 알고리즘이 대표적으로 있다. 다익스트라 알고리즘은 하나의 시작 정점에서 다른 정점까지의 최단 경로를 구한다. 플로이드 알고리즘은 모든 정점에서 다른 모든 정점까지의 최단 경로를 구한다. 가중치는 가중치 인점 행렬에 저장되어 있다고 가정하고, 직접적인 간선이 연결되어 있지 않다면 무한대값을 저장했다고 가정하자.

인접 행렬과 가중치 행렬의 차이점은 간선의 유무를 무한대로 해 두었다는 것이다. 가중치가 0인 경우도 존재할 수 있기 때문이다.

Dijkstar의 최단 경로 알고리즘

다익스트라 알고리즘은 네트워크에서 하나의 시작 정점으로부터 모든 정점까지의 최단 경로를 찾는 알고리즘이다. 최단 경로는 경로의 길이 순으로 구해진다. 먼저 집합 S를 시작 정점 v로부터의 최단 경로가 이미 발견된 정점들의 집합이라고 하자. 다익스트라 알고리즘에서는 시작 정점에서 집합 S에 있는 정점만을 거쳐서 다른 정점으로 가는 최단거리를 기록하는 distance 배열이 필요하다.

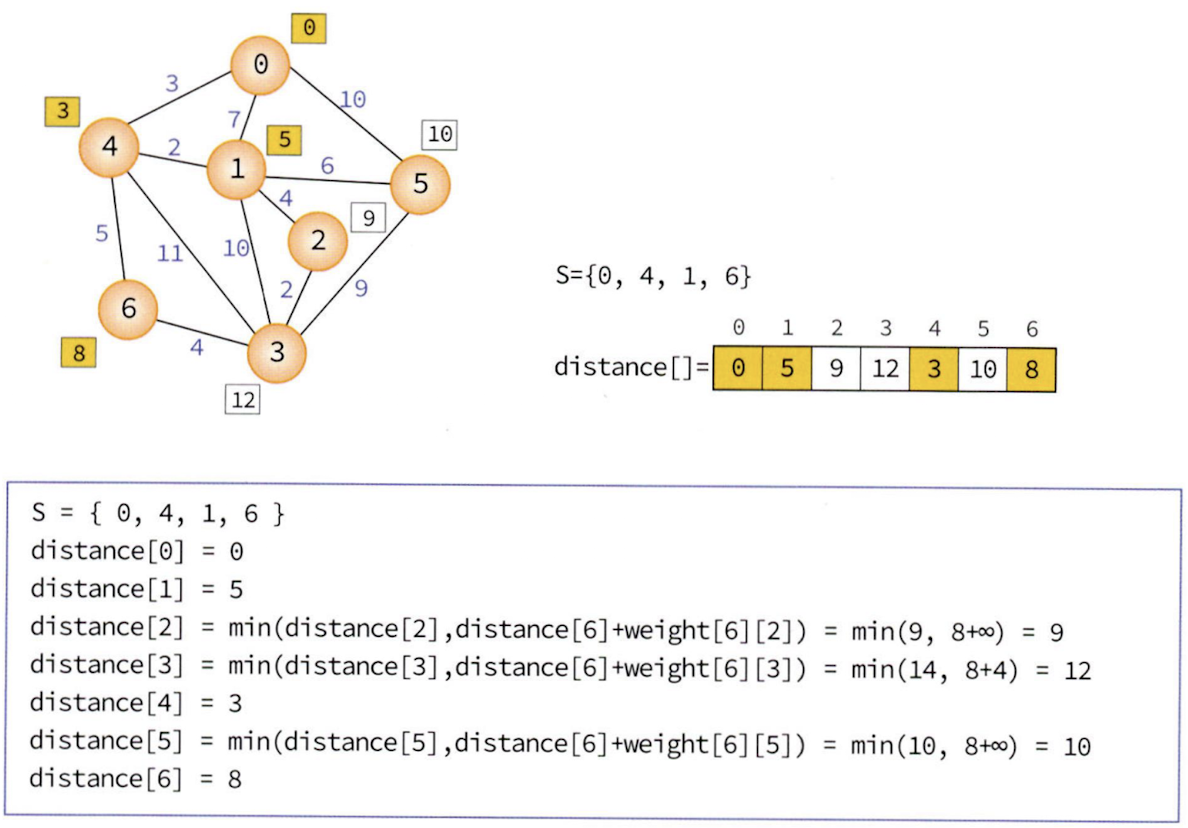
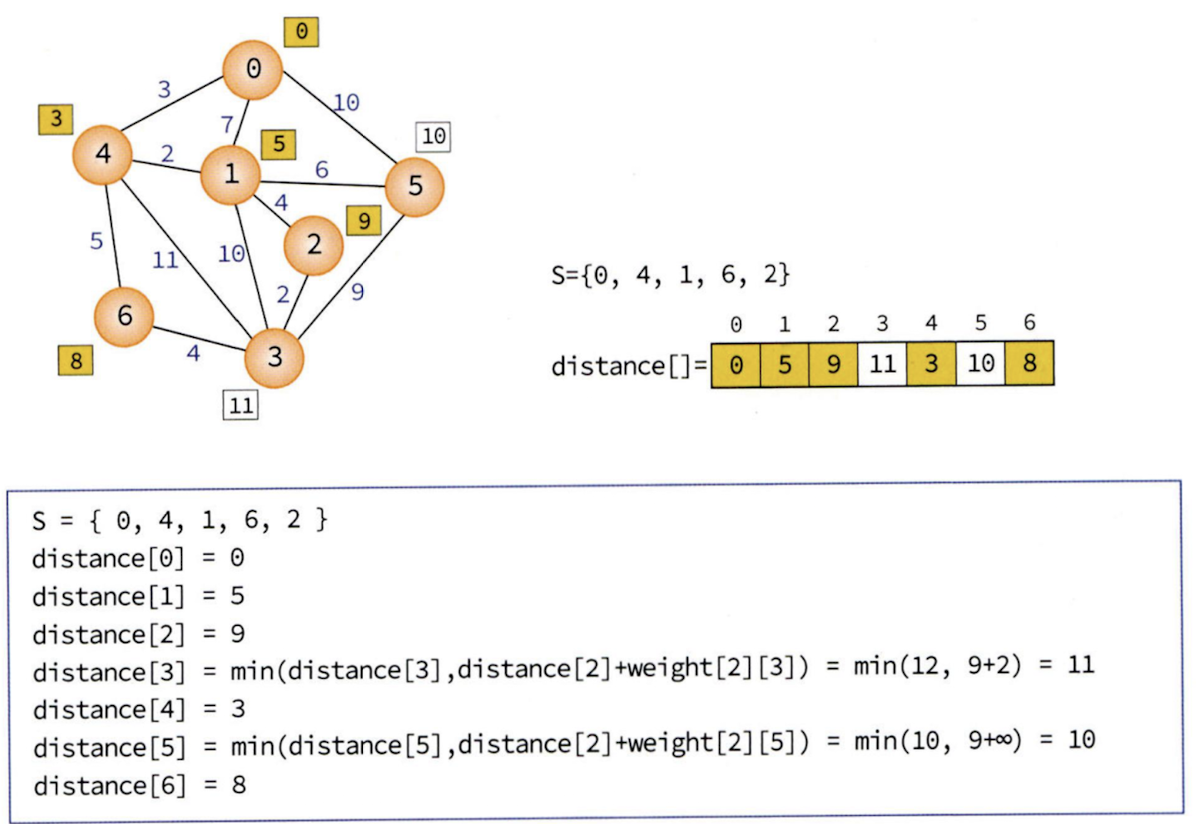
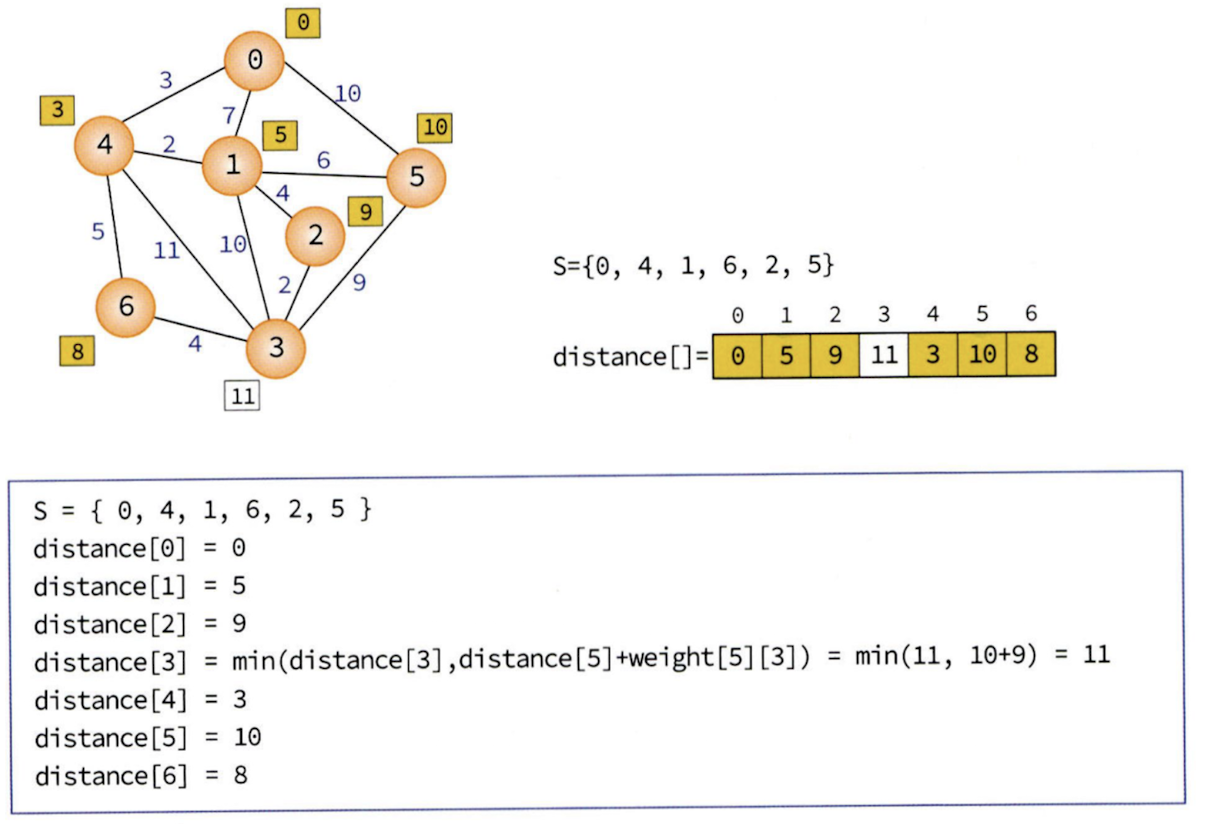
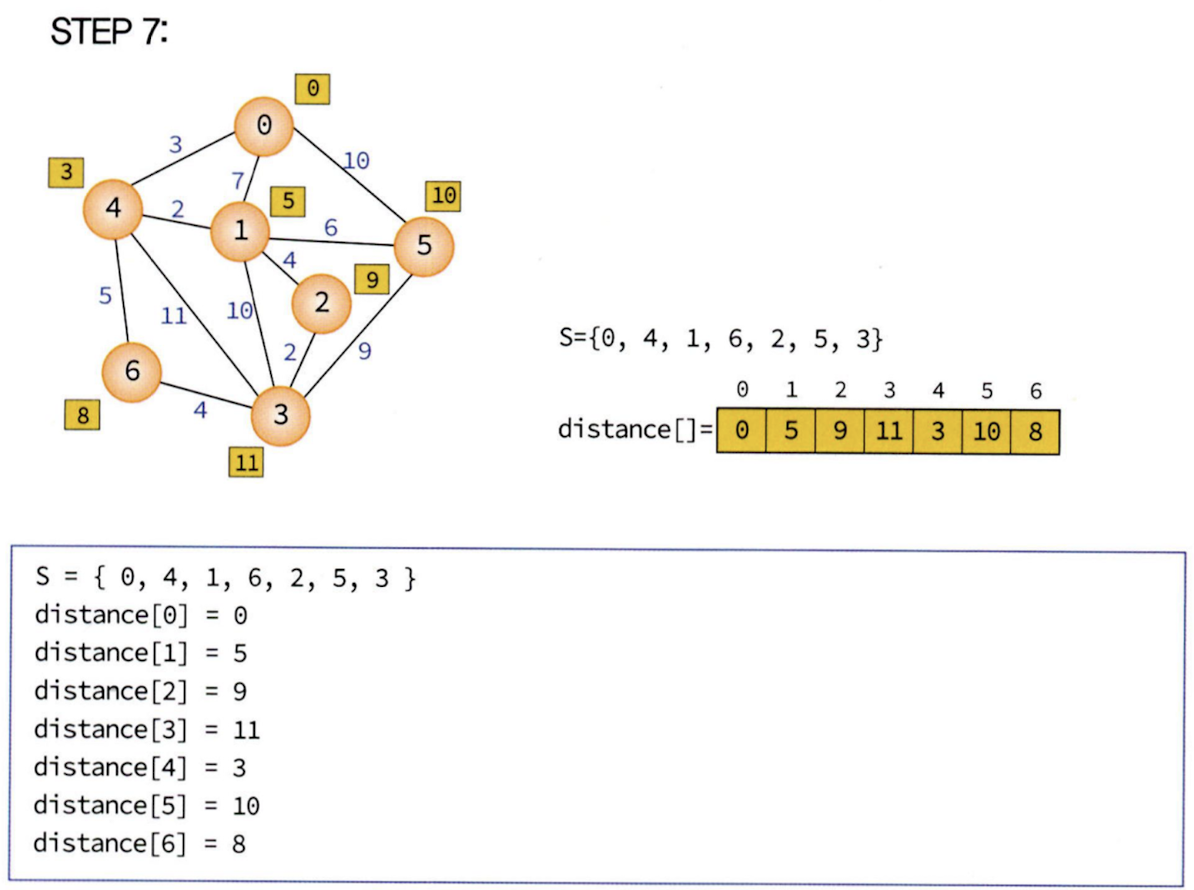
아래 단계들을 보면서 distance 배열이 어떻게 갱신되는지 확인해 보자.

Step 1

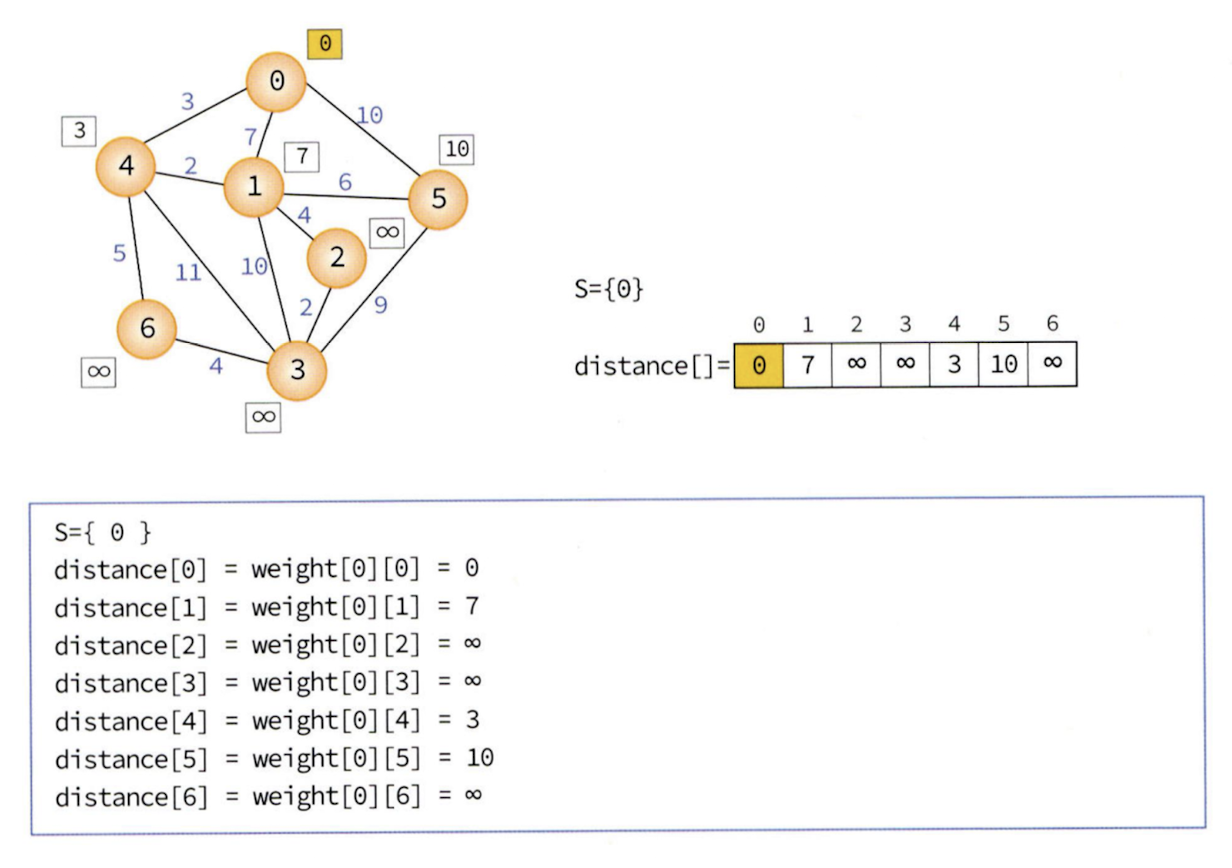
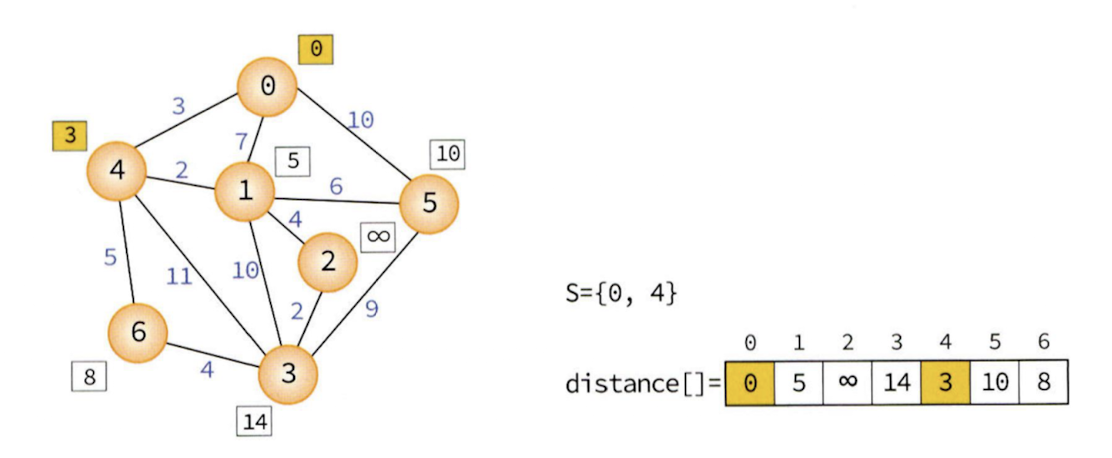
Step 2

기준 정점 0에서 가장 최단 거리는 정점 4이다. 그러면 정점 4를 경유하면 정점 0에서 목표 정점까지의 최단 거리를 알아낼 수 있으므로, 정점 4를 통해 갈 수 있는 경로값이 현재의 distance 값보다 더 작으면 갱신해준다. 따라서 Step1에서는 정점 1로 가는 거리가 7이었는데 5로 갱신된 것을 확인할 수 있다.

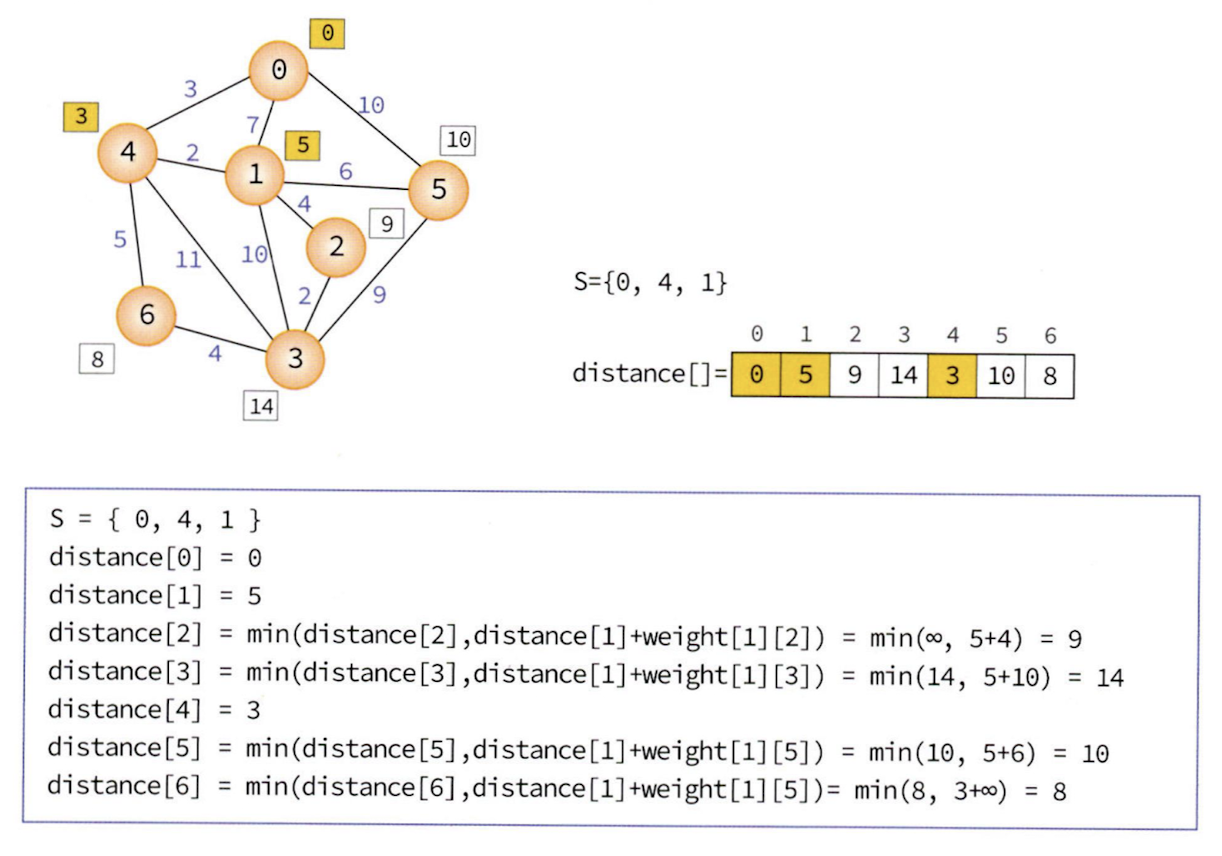
Step 3

이 과정들을 반복해주면 된다.

다익스트라 알고리즘 코드

#include <stdio.h>
#include <stdlib.h>
#include <limits.h>

#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 100
#define INF 10000000

typedef struct GraphType {
	int n;
	int weight[MAX_VERTICES][MAX_VERTICES];
} GraphType;

int distance[MAX_VERTICES];
int found[MAX_VERTICES];

// 방문하지 않은 정점 중에서 거리가 가장 짧은 인덱스 반환
int choose(int distance[], int n, int found[]) {
	int i, min, minpos;
	min = INT_MAX;
	minpos = -1;
	for(i = 0; i < n; i++)
		if (distance[i] < min && !found[i]) {
			min = distance[i];
			minpos = i;
		}
	return minpos;
}

void print_status(GraphType* g) {
	static int step = 1;
	printf("STEP %d: ", step++);
	printf("distance: ");
	for (int i = 0; i < g->n; i++) {
		if (distance[i] == INF)
			printf(" * ");
		else
			printf("%2d ", distance[i]);
	}
	printf("\n");
	printf(" found: ");
	for (int i = 0; i < g->n; i++)
		printf("%2d ", found[i]);
	printf("\n\n");
}

void shortest_path(GraphType* g, int start) {
	int i, u, w;
	for (i = 0; i < g->n; i++) {
		distance[i] = g->weight[start][i];
		found[i] = FALSE;
	}
	found[start] = TRUE;
	distance[start] = 0;
	for (i = 0; i < g->n - 1; i++) {
		print_status(g);
		u = choose(distance, g->n, found);
		found[u] = TRUE;
		for (w = 0; w < g->n; w++)
			if (!found[w])
				if (distance[u] + g->weight[u][w] < distance[w])
					distance[w] = distance[u] + g->weight[u][w];
	}
}

int main(void) {
	GraphType g = { 7,
	{{ 0,  7,  INF, INF,   3,  10, INF },
	{ 7,  0,    4,  10,   2,   6, INF },
	{ INF,  4,    0,   2, INF, INF, INF },
	{ INF, 10,    2,   0,  11,   9,   4 },
	{ 3,  2,  INF,  11,   0, INF,   5 },
	{ 10,  6,  INF,   9, INF,   0, INF },
	{ INF, INF, INF,   4,   5, INF,   0 } }
	};
	shortest_path(&g, 0);
	return 0;
}

Floyd의 최단 경로 알고리즘

그래프에 존재하는 모든 정점 사이의 최단 경로를 구하려면 다익스트라의 알고리즘을 정점의 수만큼 반복 실행하면 된다. 그러나 모든 정점 사이의 최단 거리를 구하려면 더 간단하고 좋은 알고리즘이 존재한다. 플로이드 알고리즘은 그래프에 존재하는 모든 정점 사이의 최단 경로를 한 번에 모두 찾아주는 알고리즘이다.

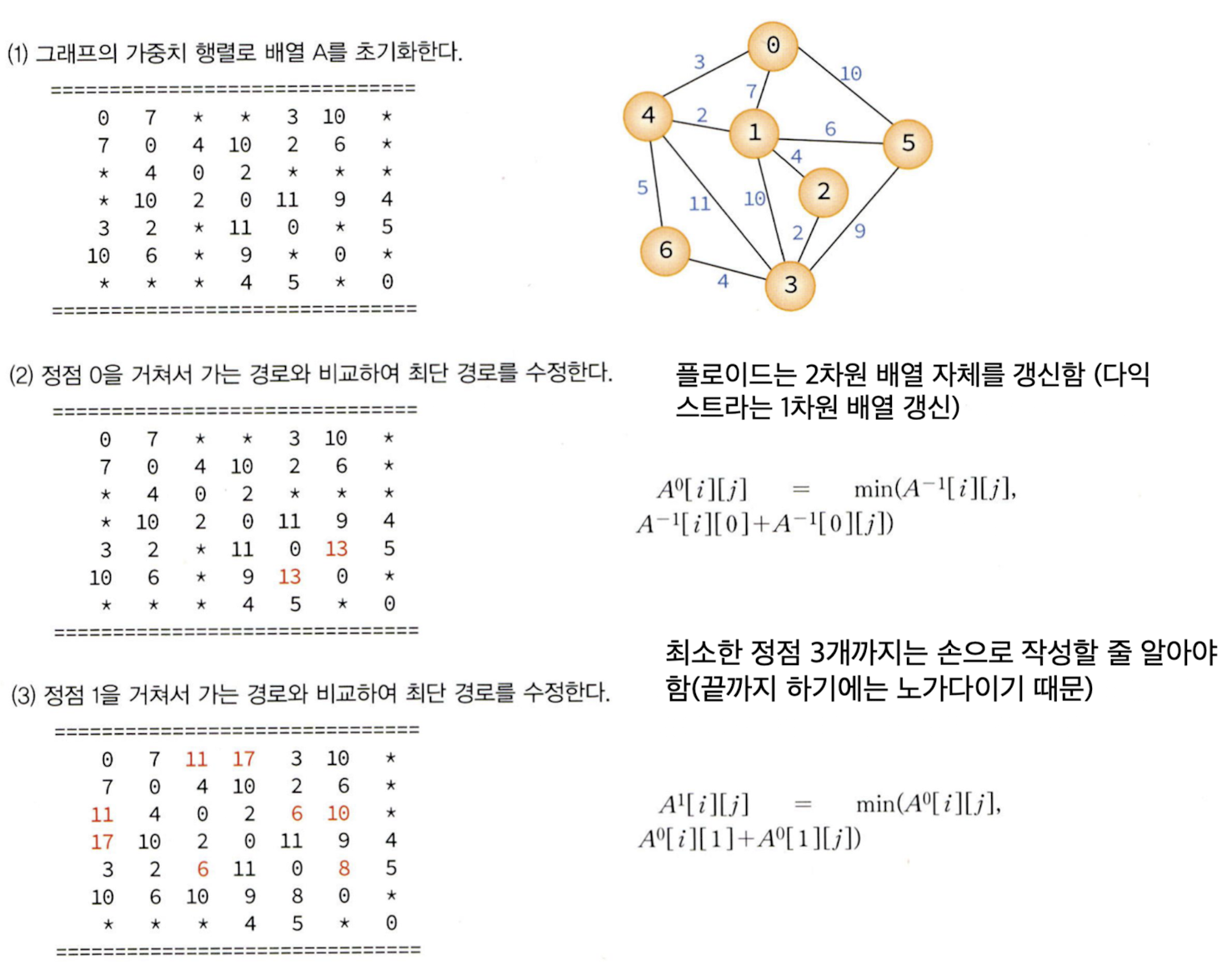
플로이드 알고리즘은 2차원 배열 A를 이용하여 3중 반복을 하는 루프로 구성되어 있다. 먼저 인접 행렬은 i == j라면 weight[i][j] = 0으로 하고 만약 두 개의 정점 i, j 사이에 간선이 존재하지 않으면 weight[i][j] == ∞\infty 라고 하자. 정점 i, j 사이에 간선이 존재하면 물론 weight[i][j]는 간선 (i, j)의 가중치가 된다. 플로이드 알고리즘은 삼중 반복문으로 표현된다.


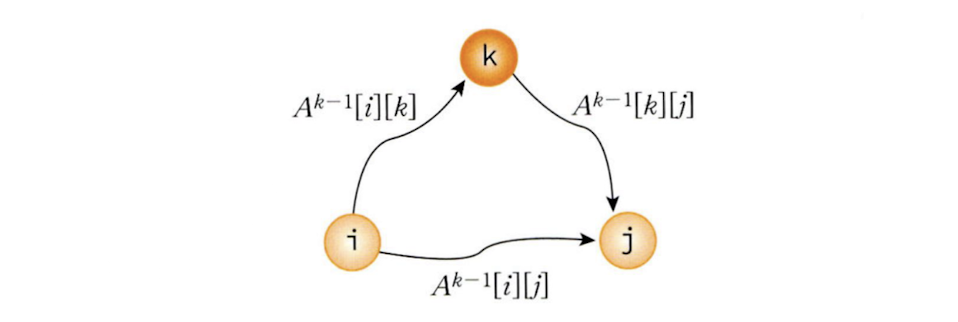
1. 정점 k를 거쳐서 가지 않는 경우
: Ak[i][j]A^k[i][j]는 k보다 큰 정점은 통과하지 않으므로 이경우 최단 거리는 Ak−1[i][j]A^{k-1}[i][j]가 된다.
2. 정점 k를 통과하는 경우
: 이 경우 i에서 k까지의 최단 거리 Ak−1[i][k]A^{k-1}[i][k]에다가 k에서 j까지의 최단 거리인 Ak−1[k][j]A^{k-1}[k][j]를 더한 값이 될 것이다.

다음은 플로이드 전체 과정을 단계별로 나타낸 것이다.

Floyd 알고리즘 전체 코드

#include <stdio.h>
#include <stdlib.h>

#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 100
#define INF 1000000

typedef struct GraphType {
	int n;
	int weight[MAX_VERTICES][MAX_VERTICES];
} GraphType;

int A[MAX_VERTICES][MAX_VERTICES];

void printA(GraphType* g) {
	int i, j;
	printf("=====================");
	for (i = 0; i < g->n; i++) {
		for (j = 0; j < g->n; j++) {
			if (A[i][j] == INF)
				printf(" * ");
			else printf("%3d ", A[i][j]);
		}
		printf("\n");
	}
	printf("=====================");
}

void floyd(GraphType* g) {
	int i, j, k;
	for (i = 0; i < g->n; i++)
		for (j = 0; j < g->n; j++)
			A[i][j] = g->weight[i][j];
	printA(g);

	for (k = 0; k < g->n; k++) { // 경유할 정점
		for (i = 0; i < g->n; i++) // 시작 정점
			for (j = 0; j < g->n; j++) // 목표 정점
				if (A[i][k] + A[k][j] < A[i][j])
					A[i][j] = A[i][k] + A[k][j];
		printA(g);
	}
}

int main(void) {
	GraphType g = { 7,
	{{ 0,  7,  INF, INF,   3,  10, INF },
	{ 7,  0,    4,  10,   2,   6, INF },
	{ INF,  4,    0,   2, INF, INF, INF },
	{ INF, 10,    2,   0,  11,   9,   4 },
	{ 3,  2,  INF,  11,   0, INF,   5 },
	{ 10,  6,  INF,   9, INF,   0, INF },
	{ INF, INF, INF,   4,   5, INF,   0 } }
	};
	floyd(&g);
	return 0;
}

다익스트라 알고리즘과 차이점

목적

다익스트라

  • 특정 시작정점으로부터 다른 모든 정점까지의 최단 경로를 구하는데 사용
  • 단일 소스 최단 경로(single-source shortest path) 문제를 해결

플로이드-워셜

  • 모든 정점 쌍 간의 최단 경로를 구하는데 사용
  • 다중 소스 최단 경로(all-source shortest path) 문제를 해결한다.

그래프 특성

다익스트라

  • 간선의 가중치가 음수가 아닌 경우에만 동작
  • 음수 가중치가 있으면 올바른 결과를 보장할 수 없음

플로이드 워셜

  • 음수 가중치가 포함된 그래프에서도 동작함
  • 단, 그래프에 음수 사이클이 존재하면 사용할 수 없음

시간 복잡도

다익스트라

  • 우선순위 큐(힙)을 사용한 경우
    : 모든 쌍의 최단 경로를 구하려면 n번 실행해야 하므로 O(E+NlogN)O(E + NlogN)이다.
  • 인접행렬 사용한 경우
    : 최단 경로 알고리즘은 주 반복문을 n번 반복하고 내부 반복문을 2n번 반복하므로 O(n2)O(n^2)의 시간 복잡도를 가진다.

플로이드-워셜

  • 시간 복잡도는 O(n3)O(n^3) 이다.

구현 방식

다익스트라

  • 그리디 알고리즘을 기반으로 함
  • 방문하지 않은 정점 중 최소 거리를 가지는 정점을 반복적으로 선택

플로이드 워셜

  • 동적 계획법을 기반으로 함
  • 중간 정점을 하나씩 추가하며, 모든 정점 쌍 간의 최단 경로를 점진적으로 갱신

사용 예시

다익스트라

  • 단일 출발지 기반 최단 경로를 계산할 때 사용
  • 예를 들어 GPS 시스템, 네트워크 라우팅 등

플로이드 워셜

  • 모든 정점 간의 관계를 알아야 하는 문제
  • 예를 들어 물류 시스템에서 최단 경로를 사전에 계산하는 경우

출처
C언어로 쉽게 풀어쓴 자료구조 - 천인구
https://loosie.tistory.com/146?utm_source=chatgpt.com
https://roytravel.tistory.com/340?utm_source=chatgpt.com

profile
이재원
20학번 새내기^^(였음..)
이전 포스트

최단 경로(Shortest Path)

다음 포스트

위상 정렬(Topological Sorting)

0개의 댓글