위상 정렬(Topological Sorting)

이재원·2024년 12월 14일

알고리즘 위상정렬

알고리즘

목록 보기

8/15

위상 정렬(Topological Sorting)

위상 정렬은 방향성이 있는 비순환 그래프(DAG)의 정점들을 선형적으로 나열하는 정렬 방법이다.

이 정렬은 그래프의 간선 방향에 따라 특정 순서를 유지해야 할 때 유용하다. 예를 들어, 작업 우선순의, 수업 과목의 선수 과목 체계, 컴파일러의 의존성 분석 등을 다룰 때 사용된다.

위상 정렬의 특징

1. DAG(Directed Acyclic Graph)

위상 정렬은 반드시 방향성이 있고 순환이 없는 그래프에서만 수행할 수 있다. 순환이 존재한다면 위상 정렬이 불가능하다.

2. 순서 보장

그래프의 간선(u → v)가 있다면 정렬 결과에서 u가 항상 v보다 앞에 나온다.

위상 정렬의 주요 알고리즘

Kahn의 알고리즘

모든 정점의 진입 차수(In-degree)를 계산한 후, 집입 차수가 0인 정점부터 처리하는 방식이다. 과정은 다음과 같다.

모든 정점의 진입 차수를 계산한다.
진입 차수가 0인 정점을 큐에 삽입한다.
큐에서 정점을 꺼내고, 그 정점과 연겨된 모든 간선을 제거하며 연결된 정점들의 진입 차수를 감소시킨다.
감소된 진입 차수가 0이 된 정점을 큐에 추가한다.
큐가 빌 때까지 과정을 반복하며, 처리된 순서가 위상 정렬 결과가 된다.

이 경우 시간 복잡도는 O(V + E)가 된다.

DFS 기반 알고리즘

DFS를 이용하여 모든 정점을 탐색하면서, 종료 시점을 기준으로 스택에 저장하는 방식이다. 과정은 다음과 같다.

모든 정점을 방문하지 않은 상태로 초기화한다.
각 정점에서 DFS를 수행한다.
DFS 탐색이 끝난 정점을 스택에 추가한다.
모든 정점에 대해 DFS를 완료한 후, 스택에서 정점을 하나씩 꺼내어 위상 정렬 순서를 생성한다.

DFS 기반으로 작성한 경우의 시간 복잡도는 Kahn의 알고리즘과 마찬가지로 O(V + E)이다.

위상 정렬 구현

선수 과목을 정렬하는 것을 예제로 하며, 위상 정렬의 구현을 단순히 하기 위해 큐 대신 스택을 사용할 것이다.

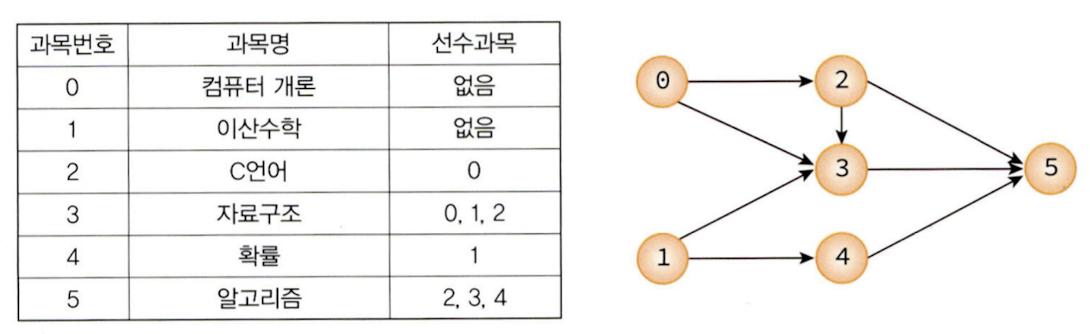
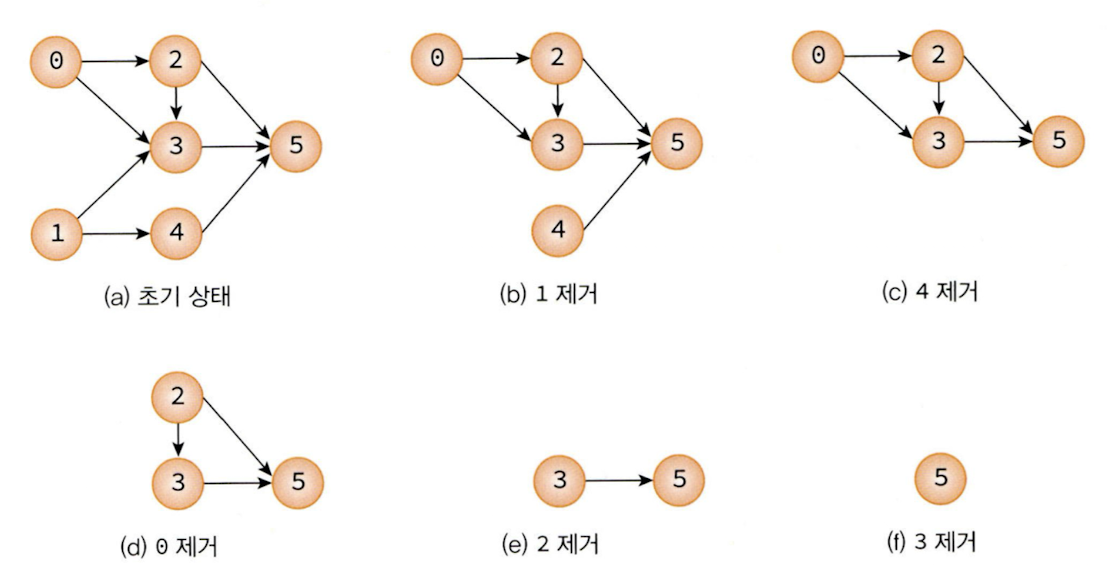
위 과목을 위상 정렬 해보면, 내차수가 0인 정점 1을 시작으로 정점 1와 간선을 제거하면, 다음 단계에서 정점 4의 진입 차수가 0이 되므로 후보 정점은 0, 4가 된다. 만약 정점 4를 선택하면 다음 단계에서는 오직 정점 0만이 후보가 된다. 다음에 정점 0이 선택되고 정점 2가 진입 차수가 0이 되어 선택 가능하게 된다. 다음에 정점 2, 정점 3, 정점 5를 선택하면 결과적으로 1, 4, 0, 2,3, 5가 된다.

전체 코드

스택

#include <stdio.h>
#include <stdlib.h>

#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 100

#define MAX_STACK_SIZE 100
typedef int element;
typedef struct {
	element stack[MAX_STACK_SIZE];
	int top;
} StackType;

// 스택 초기화 함수
void init(StackType* s)
{
	s->top = -1;
}
// 공백 상태 검출 함수
int is_empty(StackType* s)
{
	return (s->top == -1);
}
// 포화 상태 검출 함수
int is_full(StackType* s)
{
	return (s->top == (MAX_STACK_SIZE - 1));
}
// 삽입함수
void push(StackType* s, element item)
{
	if (is_full(s)) {
		fprintf(stderr, "스택 포화 에러\n");
		return;
	}
	else s->stack[++(s->top)] = item;
}
// 삭제함수
element pop(StackType* s)
{
	if (is_empty(s)) {
		fprintf(stderr, "스택 공백 에러\n");
		exit(1);
	}
	else return s->stack[(s->top)--];
}

그래프 삽입

typedef struct GraphNode {
	int vertex;
	struct GraphNode* link;
} GraphNode;

typedef struct GraphType {
	int n;
	GraphNode* adj_list[MAX_VERTICES];
} GraphType;

void graph_init(GraphType* g) {
	int v;
	g->n = 0;
	for (v = 0; v < MAX_VERTICES; v++)
		g->adj_list[v] = NULL;
}

// 정점 삽입 연산
void insert_vertex(GraphType* g, int v) {
	if (((g->n) + 1) > MAX_VERTICES) {
		fprintf(stderr, "그래프: 정점의 개수 초과");
		return;
	}
	g->n++;
}
// 간선 삽입 연산, v를 u의 인접 리스트에 삽입한다.
void insert_edge(GraphType* g, int u, int v) {
	GraphNode* node;
	if (u >= g->n || v >= g->n) {
		fprintf(stderr, "그래프: 정점 번호 오류");
		return;
	}
	node = (GraphNode*)malloc(sizeof(GraphNode));
	node->vertex = v;
	node->link = g->adj_list[u];
	g->adj_list[u] = node;
}

위상 정렬

int topo_sort(GraphType* g) {
	int i;
	StackType s;
	GraphNode* node;

	int* in_degree = (int*)malloc(g->n * sizeof(int));
	for (i = 0; i < g->n; i++)
		in_degree[i] = 0;
	for (i = 0; i < g->n; i++) {
		// 정점 i의 인접 리스트를 가져옴
		GraphNode* node = g->adj_list[i];
		while (node != NULL) {
			// i에서 node->vertex로 가는 간선이 있음을 반영
			in_degree[node->vertex]++;
			node = node->link;
		}
	}

	init(&s);
	for (i = 0; i < g->n; i++) {
		if (in_degree[i] == 0)
			push(&s, i);
	}

	while (!is_empty(&s)) {
		int w;
		w = pop(&s);
		printf("정점 %d ->", w);
		node = g->adj_list[w];
		while (node != NULL) {
			int u = node->vertex;
			in_degree[u]--;
			if (in_degree[u] == 0)
				push(&s, u);
			node = node->link;
		}
	}
	free(in_degree);
	printf("\n");
	
	return (i == g->n); 
}

마지막에 (i == g→n)을 수행하는 이유는 사이클 여부를 체크하기 위해서이다. 사이클이 있는 구조라면 일부 정점의 진입 차수가 0이 되지 않아서 처리되지 못하기 때문에, 위상 정렬이 처리된 개수인 i와 정점의 전체 개수가 일치하면 사이클이 없는 것이다. 따라서 위 비교는 위상 정렬이 정상적으로 완료되었으며, 그래프는 사이클이 없는 DAG임을 의미한다.

메인 함수

int main(void) {
	GraphType g;

	graph_init(&g);
	insert_vertex(&g, 0);
	insert_vertex(&g, 1);
	insert_vertex(&g, 2);
	insert_vertex(&g, 3);
	insert_vertex(&g, 4);
	insert_vertex(&g, 5);

	//정점 0의 인접 리스트 생성
	insert_edge(&g, 0, 2);
	insert_edge(&g, 0, 3);
	//정점 1의 인접 리스트 생성
	insert_edge(&g, 1, 3);
	insert_edge(&g, 1, 4);
	//정점 2의 인접 리스트 생성
	insert_edge(&g, 2, 3);
	insert_edge(&g, 2, 5);
	//정점 3의 인접 리스트 생성
	insert_edge(&g, 3, 5);
	//정점 4의 인접 리스트 생성
	insert_edge(&g, 4, 5);
	//위상 정렬 
	topo_sort(&g);
	// 동적 메모리 반환 코드 생략
	return 0;
}

// 실행 결과
// 정점1 -> 정점 4 -> 정점 0 -> 정점 2 -> 정점 3 -> 정점 5 ->

출처
C언어로 쉽게 풀어쓴 자료구조 - 천인구
https://coder-narak.tistory.com/34?utm_source=chatgpt.com
https://www.techiedelight.com/kahn-topological-sort-algorithm/?utm_source=chatgpt.com
https://m.blog.naver.com/sweetgirl0111/222227016242?utm_source=chatgpt.com