수식 트리(Expression tree) 구현
수식 트리란 이진 트리를 이용해서 수식을 표현해 놓은 것을 가르켜 수식 트리라고 한다.
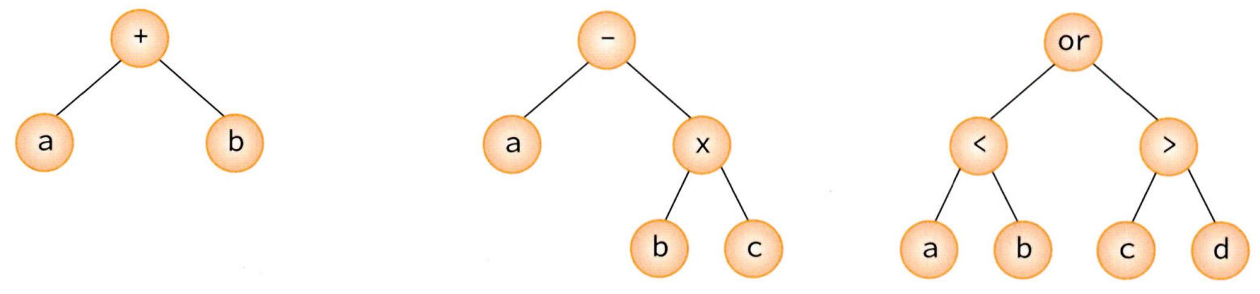
루트 노드는 연산자이고 자식 노드들은 피연산자들이다. 따라서 자식 노드들만 계산되면 전체 수식을 계산할 수 있기 때문에 순회 방식은 자식 노드들을 먼저 방문하는 후위 순회 방식으로 계산해 주면 된다.
아래는 각 순회 방식에 따라 계산되는 순서들이다.

예제 코드
#include <stdio.h>
#include <stdlib.h>
typedef struct TreeNode {
int data;
struct TreeNode* left, * right;
} TreeNode;
// +
// * +
// 1 4 16 25
TreeNode n1 = { 1, NULL, NULL };
TreeNode n2 = { 4, NULL, NULL };
TreeNode n3 = { '*', &n1, &n2 };
TreeNode n4 = { 16, NULL, NULL };
TreeNode n5 = { 25, NULL, NULL };
TreeNode n6 = { '+', &n4, &n5 };
TreeNode n7 = { '+', &n3, &n6 };
TreeNode* exp = &n7;
int evaluate(TreeNode* root) {
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return root->data;
else {
int op1 = evaluate(root->left);
int op2 = evaluate(root->right);
printf("%d %c %d을 계산합니다.\n", op1, root->data, op2);
switch (root->data)
{
case '+':
return op1 + op2;
case '-':
return op1 - op2;
case '*':
return op1 * op2;
case '/':
return op1 / op2;
}
}
return 0;
}
int main() {
printf("수식의 값은 %d입니다.\n", evaluate(exp));
return 0;
}
// 출력
// 1 * 4을 계산합니다.
// 16 + 25을 계산합니다.
// 4 + 41을 계산합니다.
// 수식의 값은 45입니다.스레드(Thread) 이진트리
이진 트리를 연결 리스트로 표현했을 때 마지막 노드들이 모두 NULL을 가리켜 메모리 낭비가 심각하다. 이를 해결하기 위한 방법이 NULL링크들이 특정 노드를 가리키도록 하는 것으로, 여기서 조정된 NULL링크를 스레드라고 한다.
스레드 이진 트리는 스택을 이용하지 않고 포인터를 이용하여 순회의 시간을 단축시킨 방식으로 중위 순회를 기본으로 한다.
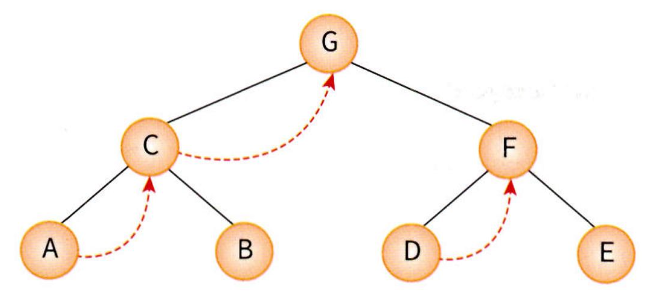
중위 순회의 경우 A를 제일 먼저 방문한다. A에서 다음으로 방문할 노드는 C이기 때문에 A의 링크를 C에 연결시킨다. 이로 인해 스택을 사용하지 않고도 반복문을 통해 A에서 C로 바로 이동할 수 있게 된다.
여기서 오른쪽 링크에만 스레드로 연결한 이유는 중위 순회의 경우 항상 왼쪽 서브 트리를 먼저 방문을 하고 오른쪽 서브 트리는 가장 나중에 방문하기 때문이다. 즉, 오른쪽 링크에서 그 다음 노드로 이동은 하지만 왼쪽 노드에서 그 다음 노드로 이동하는 경우는 없기 때문이다.
용어
- 중위 선행자(Inorder predecessor) : 중위 순회 시에 선행 노드
- 중위 후속자(Inorder successor) : 중위 순회 시에 후속 노드
- 스레드(thread): 실을 이용하여 노드들을 순회 순서대로 연결시켜 놓은 것
장점과 단점
- 장점: 순회를 빠르게 할 수 있음
- 단점: 스레드를 설정하기 위해 삽입이나 삭제 함수가 더 많은 일을 해야 함
구현
스레드 이진 트리는 NULL 링크에서 스레드가 저장된다면, 링크가 자식을 가리키는지 중위 후속자를 가리키는지 알 수 없기 때문에 구별해주는 태그가 노드 내에 존재한다.
typedef struct TreeNode {
char data;
struct TreeNode *left, *right;
int is_thread; // 스레드이면 TRUE
} TreeNode;만약 is_thread가 1인 경우에는 중위 후속자가 존재하고, 0인 경우에는 서브 트리의 가장 왼쪽 노드로 가야 한다. 왜냐하면 이 경우에는 내 자신이 루트 노드이거나 중위 후속자이거나 혹은 오른쪽 서브트리의 마지막 오른쪽 노드인 경우이기 때문이다.
TreeNode * find_successor(TreeNode * p)
{
// q는 p의 오른쪽 포인터
TreeNode * q = p->right;
// 만약 오른쪽 포인터가 NULL이거나 스레드이면 오른쪽 포인터를 반환
if (q == NULL || p->is_thread == TRUE)
return q;
// 만약 오른쪽 자식이면 다시 가장 왼쪽 노드로 이동
while (q->left != NULL) q = q->left;
return q;
}마지막으로 중위 순회를 하는 함수를 만들어 보려 한다. 첫 매개변수로는 루트 노드를 받는다.
중위 순회는 가장 왼쪽 노드부터 방문하기 때문에, 왼쪽 자식이 NULL이 될 때까지 왼쪽 링크를 타고 계속 이동해야 한다.
전체 코드
#include <stdio.h>
#define TRUE 1
#define FALSE 0
typedef struct TreeNode {
char data;
struct TreeNode *left, *right;
int is_thread; // 스레드이면 TRUE
} TreeNode;
// G
// C F
// A B D E
TreeNode n1 = { 'A', NULL, NULL, 1 };
TreeNode n2 = { 'B', NULL, NULL, 1 };
TreeNode n3 = { 'C', &n1, &n2, 0 };
TreeNode n4 = { 'D', NULL, NULL, 1 };
TreeNode n5 = { 'E', NULL, NULL, 0 };
TreeNode n6 = { 'F', &n4, &n5, 0 };
TreeNode n7 = { 'G', &n3, &n6, 0 };
TreeNode * exp = &n7;
TreeNode * find_successor(TreeNode * p)
{
// q는 p의 오른쪽 포인터
TreeNode * q = p->right;
// 만약 오른쪽 포인터가 NULL이거나 스레드이면 오른쪽 포인터를 반환
if (q == NULL || p->is_thread == TRUE)
return q;
// 만약 오른쪽 자식이면 다시 가장 왼쪽 노드로 이동
while (q->left != NULL) q = q->left;
return q;
}
void thread_inorder(TreeNode * t)
{
TreeNode * q;
q = t;
while (q->left) q = q->left;// 가장 왼쪽 노드로 간다.
do {
printf("%c -> ", q->data);// 데이터 출력
q = find_successor(q); // 후속자 함수 호출
} while (q); // NULL이 아니면
}
int main(void)
{
// 스레드 설정
n1.right = &n3;
n2.right = &n7;
n4.right = &n6;
// 중위 순회
thread_inorder(exp);
printf("\n");
return 0;
}출처
C언어로 쉽게 풀어쓴 자료구조 - 천인구
https://howudong.tistory.com/120
https://limecoding.tistory.com/96
https://mattlee.tistory.com/29
