자료구조
1.원형 연결 리스트(circular linked list)
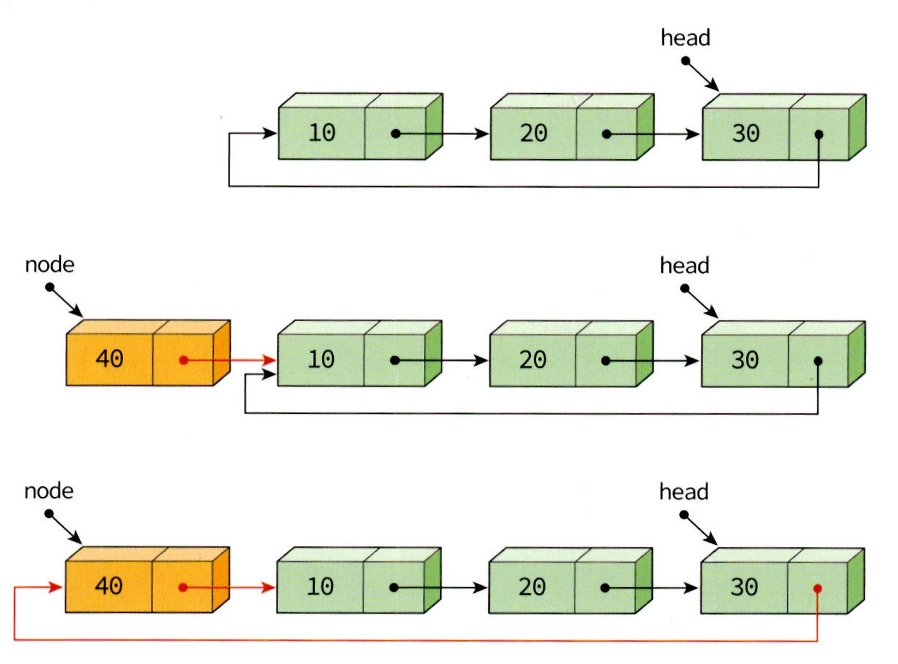
원형 연결 리스트는 마지막 노드가 첫 번째 노드를 가리키는 리스트이다. 즉, 마지막 노드의 링크가 NULL이 아닌 첫 번째 노드 주소를 가리키는 리스트이다.하나의 노드에서 다른 노드로의 접근이 가능노드의 삽입과 삭제가 단순 연결리스트보다 용이함단순 연결 리스트처럼 he
2.이중 연결 리스트(Doubly linked list)

이중 연결 리스트는 한쪽으로만 노드를 연결하는 것이 아닌 양방향으로 연결한 리스트를 말한다.실제 응용에서는 위 그림처럼 이중 연결리스트와 원형 연결리스트를 혼합한 형태가 많이 사용된다. 또한 헤드 노드(head node)라는 더미 노드가 추가되는 경우도 많다.헤드 포인
3.연결 리스트를 이용한 스택
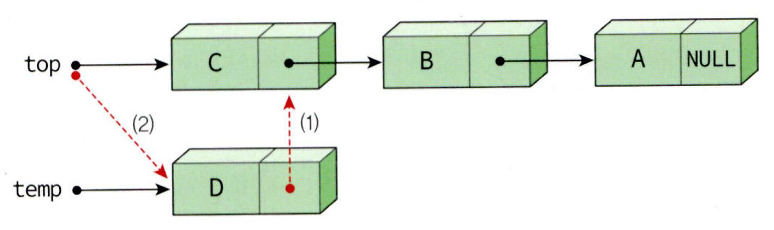
배열로 구현한 스택과 외부 인터페이스는 완전히 동일하나 내부 구현을 배열이 아닌 연결 리스트로 하는 것이다. 연결 리스트로 스택을 구현하면 다음과 같은 장점이 있다.장점: 동적 메모리 할당만 할 수 있다면 크기가 제한되지 않는다.단점: 동적 메모리 해제를 해야 하기 때
4.연결 리스트로 구현한 큐

연결 리스트로 큐를 구현하면 배열로 구현한 큐에 비해 크기가 제한되지 않는다는 장점이 있다. 다만, 메모리 공간을 더 많이 차지하고 삽입과 삭제시 좀 더 오래 걸린다는 단점이 있다.단순 연결 리스트에 front와 rear 포인터를 추가한 것과 같다. 큐에 요소가 없는
5.트리(Tree)
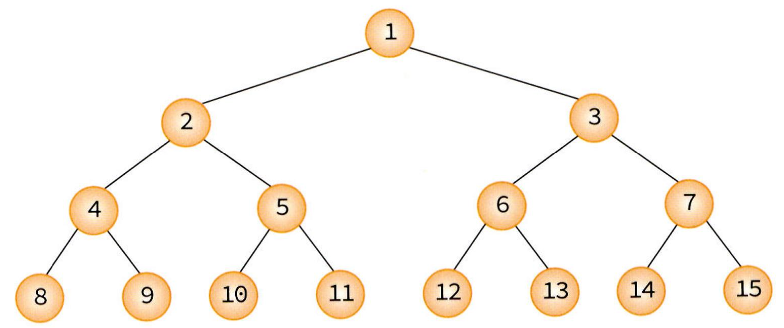
연결 리스트로 큐를 구현하면 배열로 구현한 큐에 비해 크기가 제한되지 않는다는 장점이 있다. 다만, 메모리 공간을 더 많이 차지하고 삽입과 삭제시 좀 더 오래 걸린다는 단점이 있다.단순 연결 리스트에 front와 rear 포인터를 추가한 것과 같다. 큐에 요소가 없는
6.트리의 응용(수식 트리, 스레드 트리)
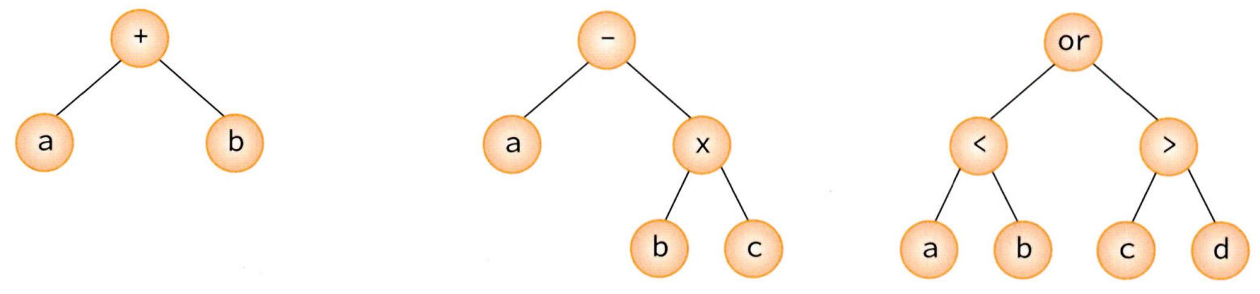
수식 트리란 이진 트리를 이용해서 수식을 표현해 놓은 것을 가르켜 수식 트리라고 한다.루트 노드는 연산자이고 자식 노드들은 피연산자들이다. 따라서 자식 노드들만 계산되면 전체 수식을 계산할 수 있기 때문에 순회 방식은 자식 노드들을 먼저 방문하는 후위 순회 방식으로 계
7.이진 탐색 트리(Binary Search Tree)
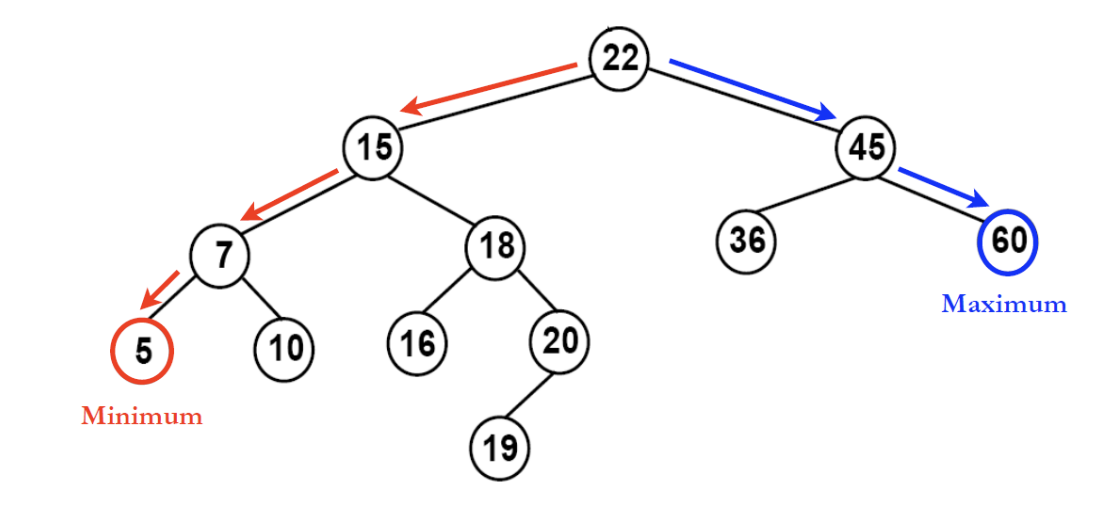
이진 탐색 트리는 모든 원소가 유일한 키를 갖으며, 왼쪽 서브 트리의 키들은 모두 루트 키보다 작고, 오른쪽 서브 트리의 키들은 모두 루트의 키보다 큰 트리를 말한다.위 그림처럼 루트 노드의 키값 22를 기준으로 왼쪽 서브 트리의 키값은 15로 22보다 작고, 오른쪽
8.그래프(Graph
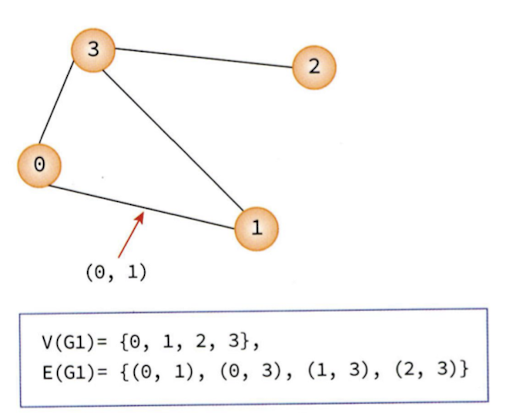
그래프는 객체 사이의 연결 관계를 표현할 수 있는 자료 구조이다. 그래프는 1736년에 수학자 오일러가 “Konigsber의 다리” 문제를 해결하기 위해 처음으로 사용했다고 한다.그래프로 표현할 수 있는 것들로는 도로, 미로, 네트워크 등이 있다.그래프는 정점(vert
9.우선순위 큐(priority queue)

우선순위 큐는 말 그대로 우선순위를 가진 큐이다. 원래의 큐는 선입선출(FIFO) 원칙에 의하여 먼저 들어온 데이터가 먼저 나가게 된다. 하지만 우선순위 큐에서는 우선 순위가 높은 데이터가 먼처 출력된다.우선순위 큐는 사실 가장 일반적인 큐라 할 수 있는데 스택이나 큐