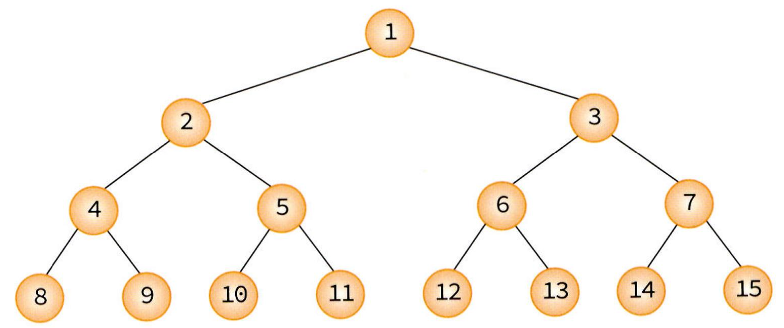
트리(Tree)
트리는 그래프의 일종으로 정점과 간선을 이용하여 데이터의 배치 형태를 추상화한 자료구조이다.
간단한 예시로는 컴퓨터의 디렉토리가 있으며, 실제 나무를 거꾸로 한 것 같은 모양을 하고 있어 트리라고 부른다.
사용되는 용어
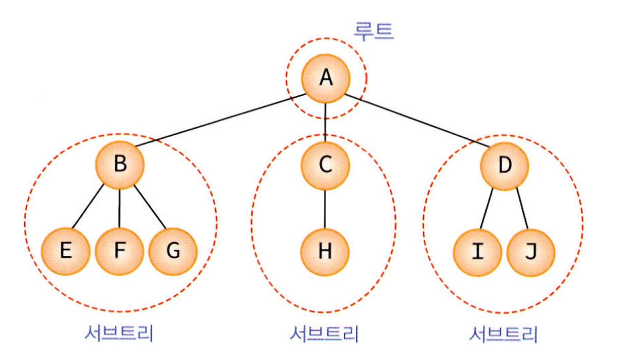
노드(Node)
- 트리의 기본 구성 요소(A, B, C, D, E, F , G, H, I, J)
간선(Edge)
- 노드와 노드 간의 연결선
루트 노드(Root Node)
- 트리 구조에서 부모가 없는 최상위 노드(A노드)
부모 노드(Parent Node)
- 자식 노드를 가진 노드
형제 노드(Slibling node)
- 같은 부모를 가지는 노드
단말 노드(terminal node)
- 자식 노드가 없는 노드
비단말노드(non-terminal node)
- 자식 노드 하나 이상 가진 노드
서브 트리(Sub tree)
- 전체에 속하는 하위 트리들
깊이(depth)
- 루트에서 어떤 노드까지의 간선의 갯수
- 따라서, 루트 노드의 깊이는 0이다.
차수(degree)
- 노드의 자식 수(A에서 B, C, D로 나눠지므로 A의 차수는 3가 된다.)
높이(height)
- 루트 노드로부터 가장 멀리 있는 단말 노드의 깊이. 즉, 깊이 중 최댓값(A의 높이는 3)
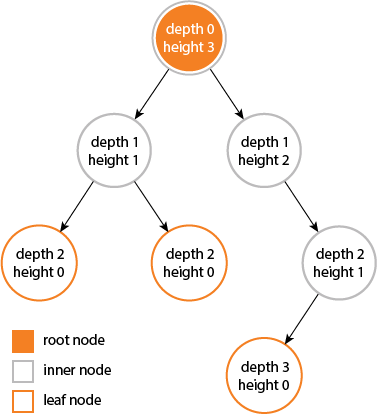
출처: https://yoongrammer.tistory.com/68
트리의 특징
- 일반적으로 대상 정보의 각 항목들을 계층적으로 구조화할 때 사용하는 비선형 자료구조이다.
- 하나의 루트 노드와 0개 이상의 하위 트리로 구성되어 있다.
- 루트 노드를 제외하고, 모든 자식 노드는 하나의 부모 노드만 갖는다.
- 트리는 데이터의 저장의 의미보다는 저장된 데이터를 더 효과적으로 탐색하기 위해 사용된다.
- 트리는 사이클이 없다.
- 트리 내에 또 다른 트리가 있는 재귀적 자료구조이다.
- 단순 순환(Loop)을 갖지 않고 연결된 무방향 그래프 구조이다.
- 루트에서 어떤 노드로 가는 경로는 반드시 하나이다.
트리의 종류
- 편향 트리: 모든 노드들이 자식을 하나만 가진 트리
- 이진 트리: 각 노드의 차수가 2이하인 트리
- 균형 트리(Balanced Tree): m형 탐색 트리에서 높이 균형을 유지하는 트리
트리의 순회
트리의 탐색 방법은 노드를 탐색하는 순서에 따라 전위 순회, 중위 순회, 후위 순회 3가지가 있다.
전위 순회(Preorder)
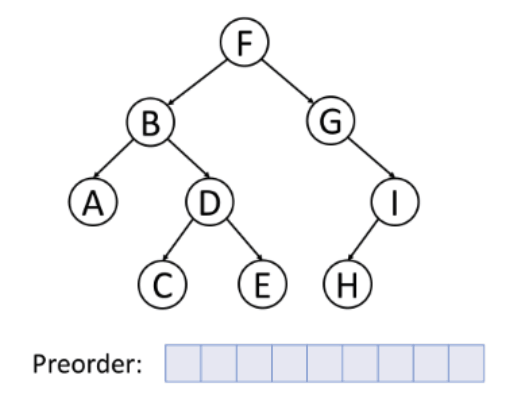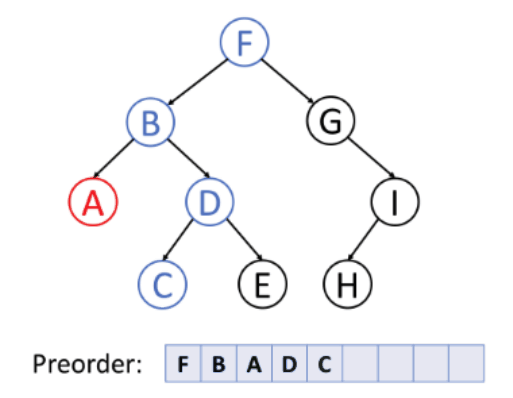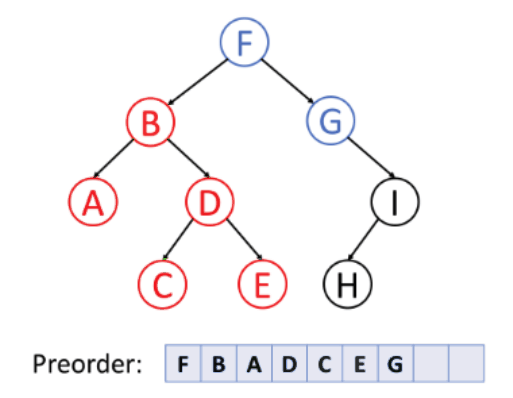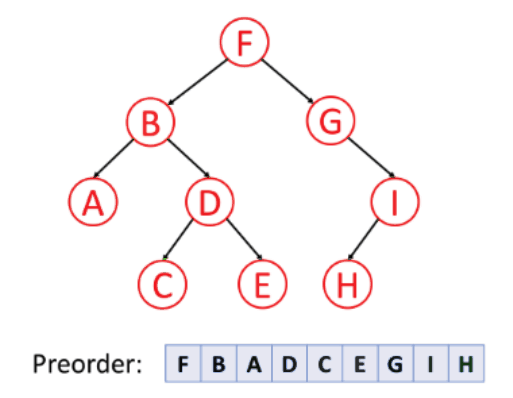
전위 순회의 탐색 순서는 다음과 같다.(F→B→A→D→C→E→G→I→H)
- 루트 노드를 방문한다.
- 왼쪽 서브 트리를 방문한다.
- 오른쪽 서브 트리를 방문한다.
중위 순회(Inorder)
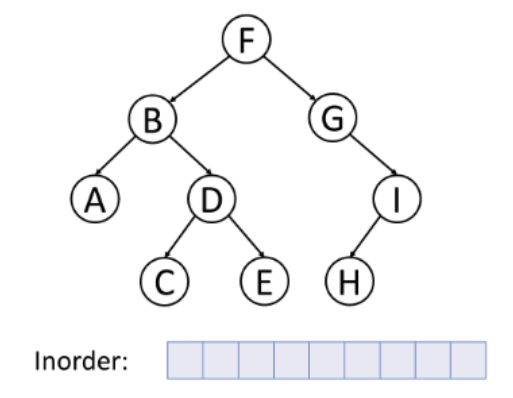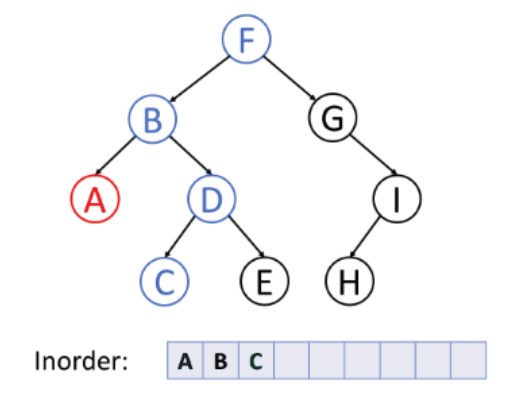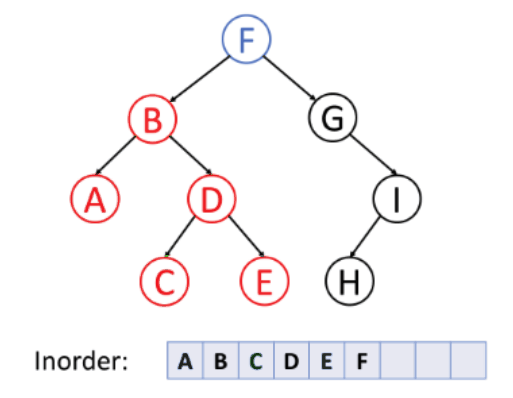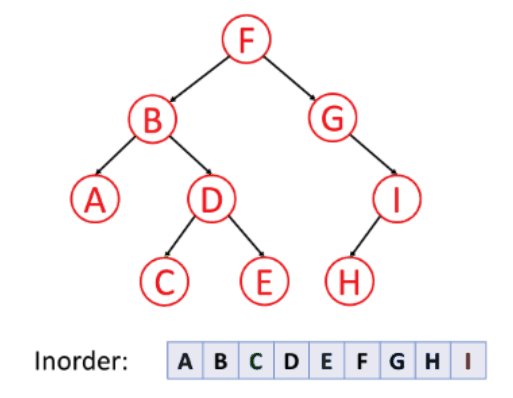
탐색 방법(A→b→C→D→E→G→H→I)
- 왼쪽 서브 트리를 방문한다.
- 루트 노드를 방문한다.
- 오른쪽 서브트리를 방문한다.
후위 순외(Postorder)
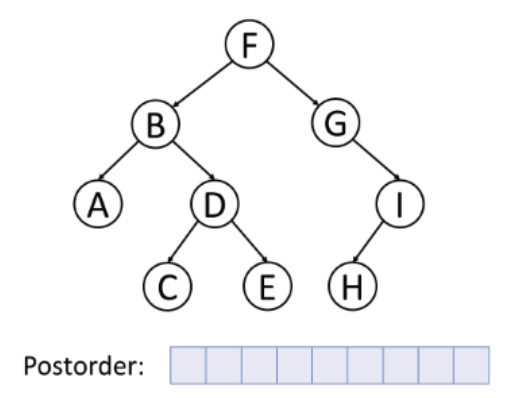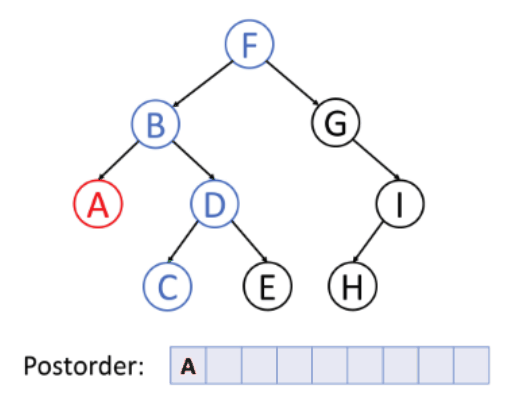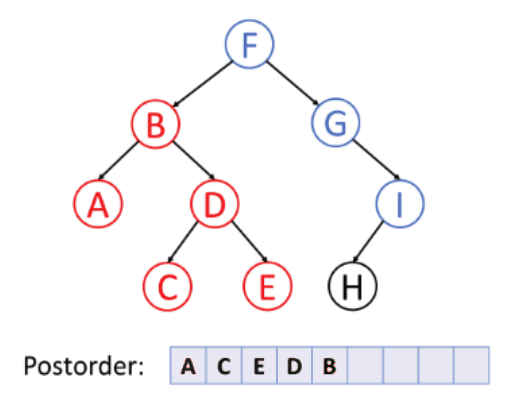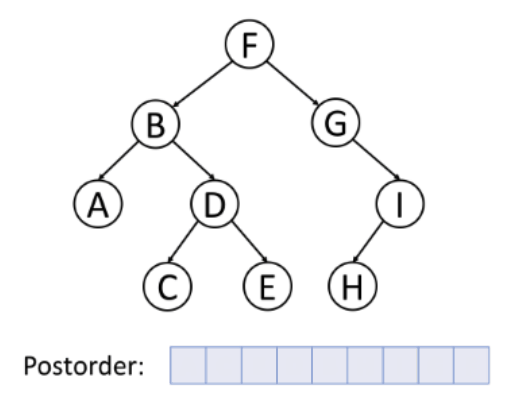
탐색 방법(A→C→E→D→B→H→I→G→F)
- 왼쪽 서브 트리의 모든 노드를 방문한다.
- 오른쪽 서브 트리의 모든 노드를 방문한다.
- 루트 노드를 방문한다.
이진 트리
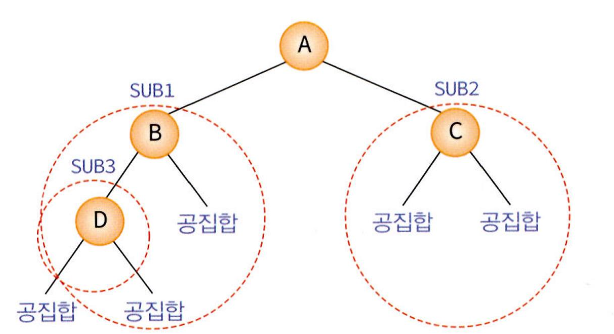
- 모든 노드가 2개의 자식 노드를 가지는 트리이다. 따라서 모든 노드의 차수는 2 이하이다.
- 자식 노드들도 모두 이진트리이다.
- 자식 노드는 공집합일 수 있다
- 공집합도 이진트리이다.
- 서브 트리간의 순서가 존재한다.
이진 트리의 특징
- 노드가 n개인 트리의 간선의 개수는 n-1개이다.
- 높이가 h인 이진트리의 경우, 최소 h개의 노드를 가지며 최대 개의 노드를 가진다.
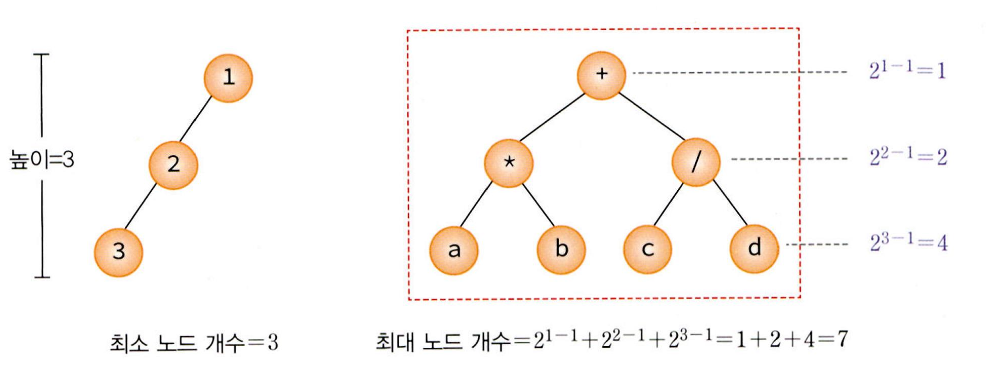
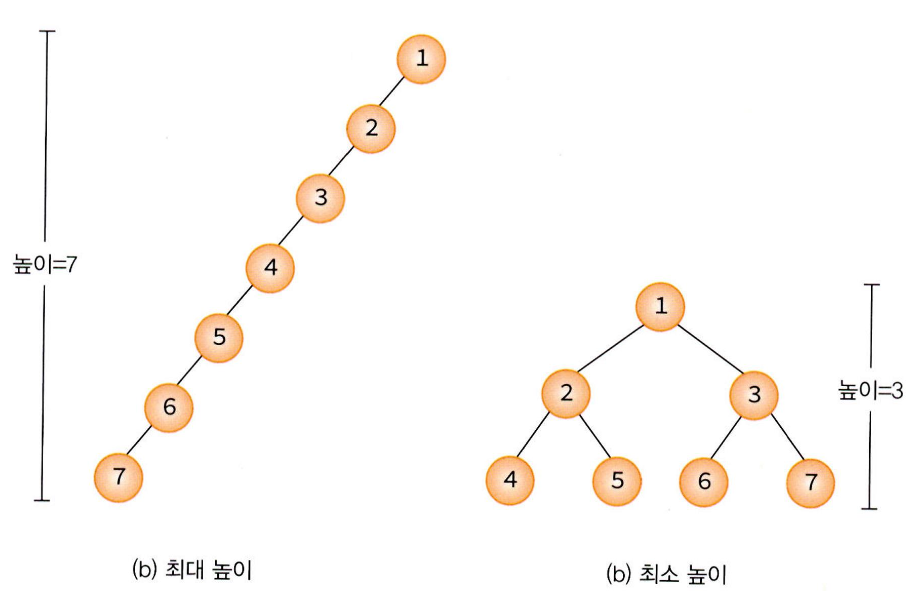
- n개의 노드를 가지는 이진트리의 높이는 최대 n이거나 최소 이 된다.
이진 트리의 분류
포화 이진 트리(Full Binary tree)
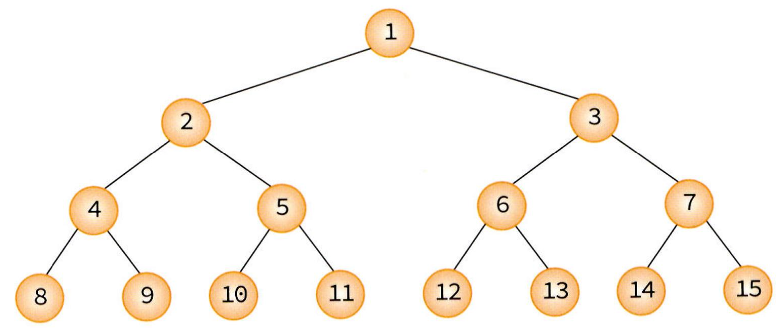
- 트리의 각 레벨에 노드가 꽉 차있는 이진트리를 의미
- 높이가 k인 포화 이진 트리는 정확하게 개의 노드를 가진다.
- 모든 노드가 두 개의 자식 노드를 가진다.
- 포화 이진 트리는 왼쪽부터 오른쪽으로 번호를 붙인다.
완전 이진 트리(complete binary tree)
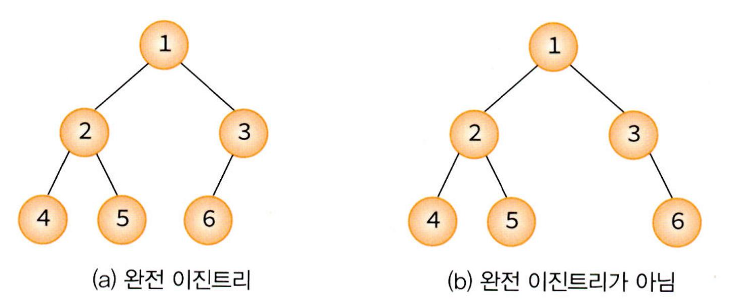
- 트리의 모든 높이에서 노드가 꽉 차 있는 이진 트리로 마지막 레벨을 제외하고는 모든 레벨이 완전히 채워져 있다.
- 마지막 레벨은 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
이진 트리의 구현
배열을 활용한 구현
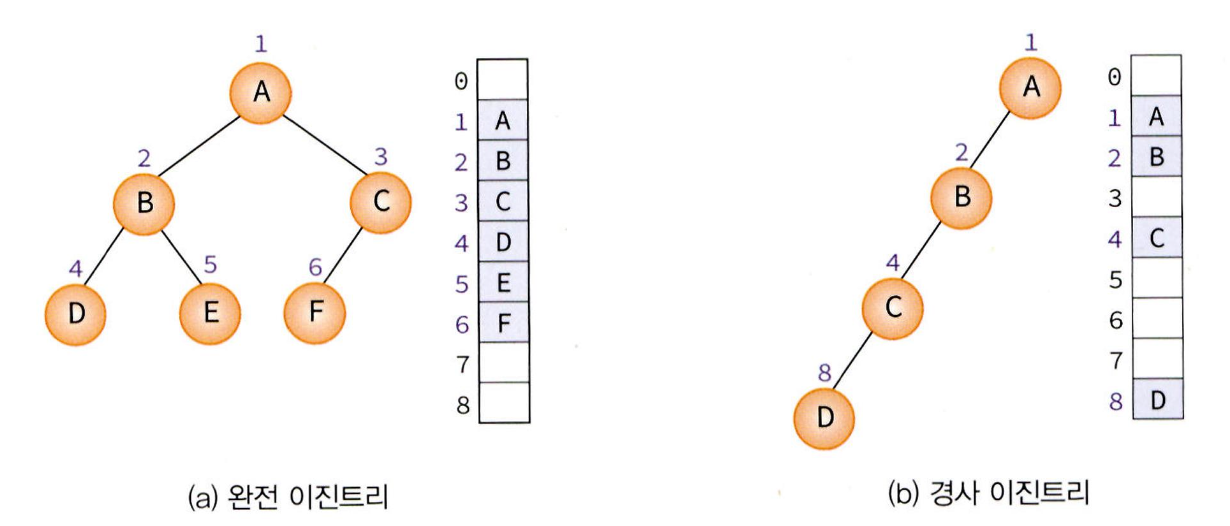
배열을 사용하여 구현할 때는 인덱스만 알면 노드의 부모자 자식을 쉽게 알 수 있다.
- 노드 i의 부모 인덱스 = i/2
- 노드 i의 왼쪽 자식 노드 인덱스 = 2i
- 노드 i의 오른쪽 자식 노드 인덱스 = 2i + 1
즉 배열로 트리를 구현할 때는 배열이라는 자료구조를 활용하여 트리를 개념적으로 생각하면 된다.
연결 리스트를 활용한 구현
연결 리스트로 트리를 구현할 때는 양방향 연결 리스트를 활용해 주면 된다.
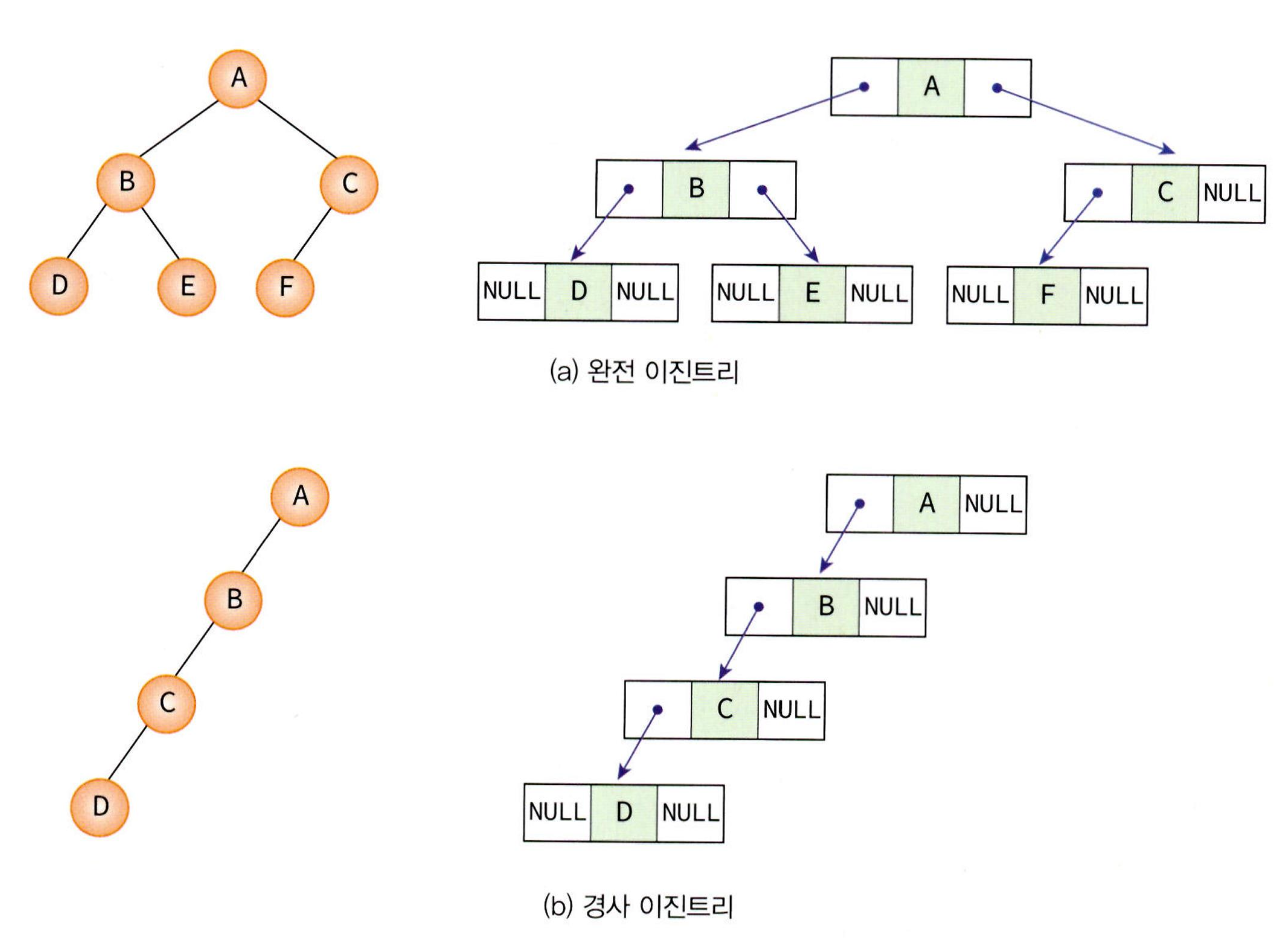
예제 1
#include <memory.h>
#include <stdio.h>
#include <stdlib.h>
typedef struct TreeNode {
int data;
struct TreeNode* left, * right;
} TreeNode;
// 15
// 4 20
// 1 16 25
TreeNode n1 = { 1, NULL, NULL };
TreeNode n2 = { 4, &n1, NULL };
TreeNode n3 = { 16, NULL, NULL };
TreeNode n4 = { 25, NULL, NULL };
TreeNode n5 = { 20, &n3, &n4 };
TreeNode n6 = { 15, &n2, &n5 };
TreeNode* root = &n6;
void inorder(TreeNode* root) {
if (root != NULL) {
inorder(root->left); // 왼쪽 자식 노드 순회
printf("[%d] ", root->data); // 노드 방문 및 출력
inorder(root->right); // 오른쪽 자식 노드 순회
}
}
void preorder(TreeNode* root) {
if (root != NULL) {
printf("[%d ", root->data); // 노드 방문 및 출력
preorder(root->left); // 왼쪽 자식 노드 순회
preorder(root->right); // 오른쪽 자식 노드 순회
}
}
void postorder(TreeNode* root) {
if (root != NULL) {
postorder(root->left); // 왼쪽 자식 노드 순회
postorder(root->right); // 오른쪽 자식 노드 순회
printf("[%d] ", root->data); // 노드 방문 및 출력
}
}
int main() {
printf("중위 순회: ");
inorder(root);
printf("\n");
printf("전위 순회: ");
preorder(root);
printf("\n");
printf("후위 순회: ");
postorder(root);
printf("\n");
return 0;
}
// 출력
// 중위 순회=[1] [4] [15] [16] [20] [25]
// 전위 순회=[15] [4] [1] [20] [16] [25]
// 후위 순회=[1] [4] [16] [25] [20] [15]이진 트리는 여러개의 이진 트리가 하나로 연결되어 있는 것과 같기 때문에 재귀 호출을 이용하여 탐색할 수 있다.
printf("[%d] ", root->data); 의 순서를 전위, 중위, 후위 순회의 특징에 알맞게 배치해 주면 쉽게 구현이 가능하다.
반복문을 사용하여 순회도 가능한데, 이 경우에는 스택을 활용해 줘야 한다.
예제 2
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
typedef struct TreeNode {
int data;
struct TreeNode *left, *right;
} TreeNode;
#define SIZE 100
int top = -1;
TreeNode *stack[SIZE];
void push(TreeNode *p)
{
if (top < SIZE - 1)
stack[++top] = p;
}
TreeNode *pop()
{
TreeNode *p = NULL;
if (top >= 0)
p = stack[top--];
return p;
}
void inorder_iter(TreeNode *root)
{
while (1) {
for (; root; root = root->left)
push(root);
root = pop();
if (!root) break;
printf("[%d] ", root->data);
root = root->right;
}
}
// 15
// 4 20
// 1 16 25
TreeNode n1 = { 1, NULL, NULL };
TreeNode n2 = { 4, &n1, NULL };
TreeNode n3 = { 16, NULL, NULL };
TreeNode n4 = { 25, NULL, NULL };
TreeNode n5 = { 20, &n3, &n4 };
TreeNode n6 = { 15, &n2, &n5 };
TreeNode *root = &n6;
int main(void)
{
printf("중위 순회=");
inorder_iter(root);
printf("\n");
return 0;
}
// 출력
// 중위 순회=[1] [4] [15] [16] [20] [25]레벨 순회
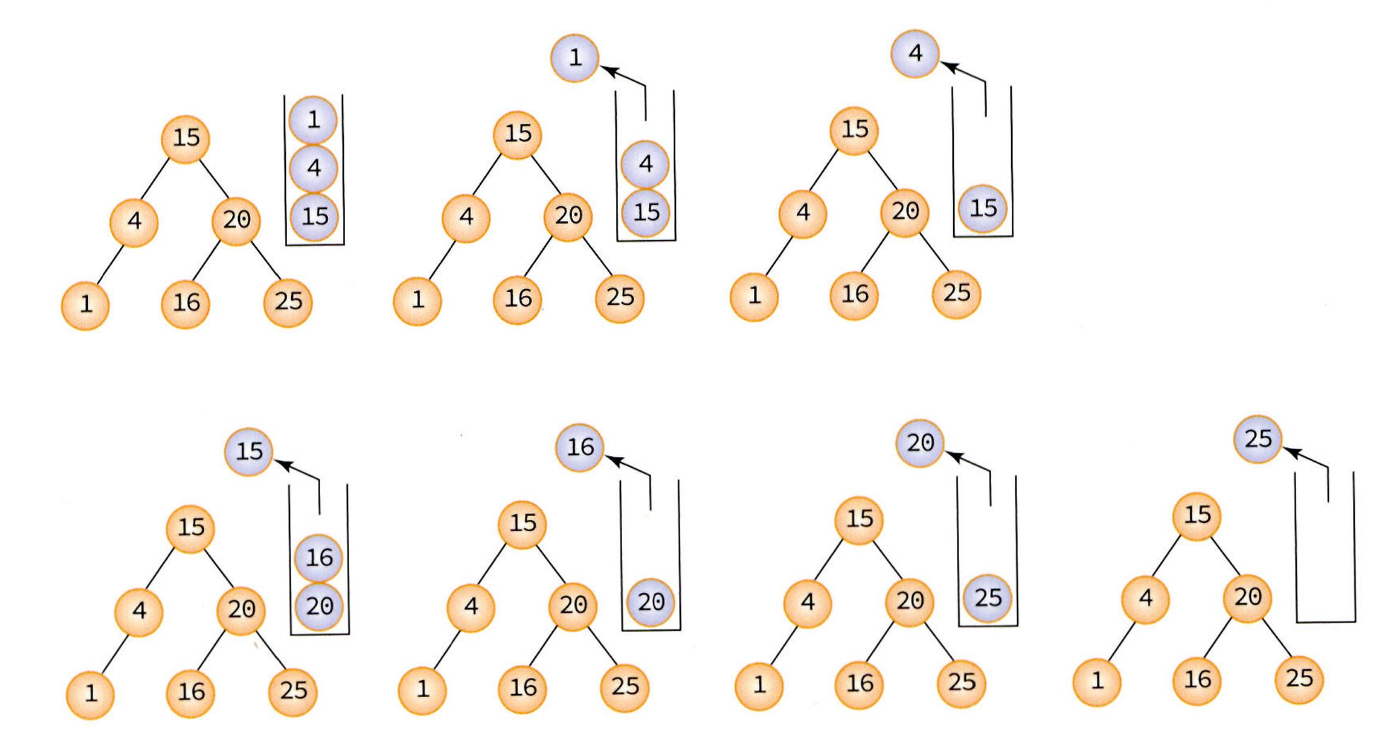
- 표준적인 순회 방법은 아니지만, 종종 사용된다.
- 레벨 순으로 검사하는 순회 방법이다.
- 큐를 사용하여 구현한다.
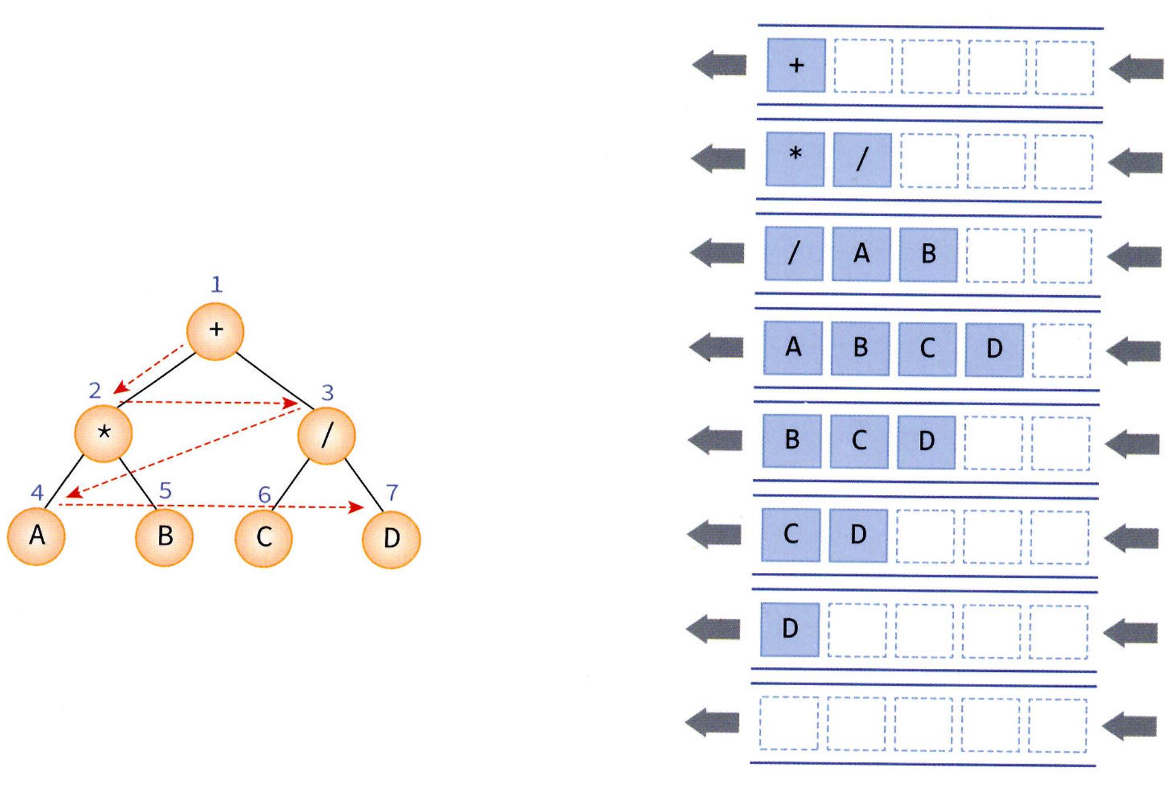
탐색 순서는 다음과 같다.
- 루트 노드인 +가 큐에 입력된 상태로 시작된다.
- 큐에서 하나 삭제하면 +가 나오게 되고 +를 방문한다.
- 노드 +의 자식 노드인 *와 / 노드를 큐에 삽입한다.
- 1~3번 과정을 반복한다.
원형 큐 구현
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
typedef struct TreeNode {
int data;
struct TreeNode* left, * right;
} TreeNode;
#define MAX_QUEUE_SIZE 100
typedef TreeNode* element;
typedef struct {
element data[MAX_QUEUE_SIZE];
int front, rear;
} QueueType;
void error(char* message) {
fprintf(stderr, "%s\n", message);
exit(1);
}
void init_queue(QueueType* q) {
q->front = q->rear = 0;
}
int is_empty(QueueType* q) {
return (q->front == q->rear);
}
int is_full(QueueType* q) {
return ((q->rear + 1) % MAX_QUEUE_SIZE == q->front);
}
void enqueue(QueueType* q, element item) {
if (is_full(q))
error("큐가 포화 상태입니다.");
q->rear = (q->rear + 1) % MAX_QUEUE_SIZE;
q->data[q->rear] = item;
}
element dequeue(QueueType* q) {
if (is_empty(q))
error("큐가 공백상태입니다.");
q->front = (q->front + 1) % MAX_QUEUE_SIZE;
return q->data[q->front];
}먼저 원형 큐 구조체를 선언해주고 관련된 함수들을 구현해준다.
여기서 MAX_QUEUE_SIZE로 나눠주는 이유를 간략하게 설명해 보면
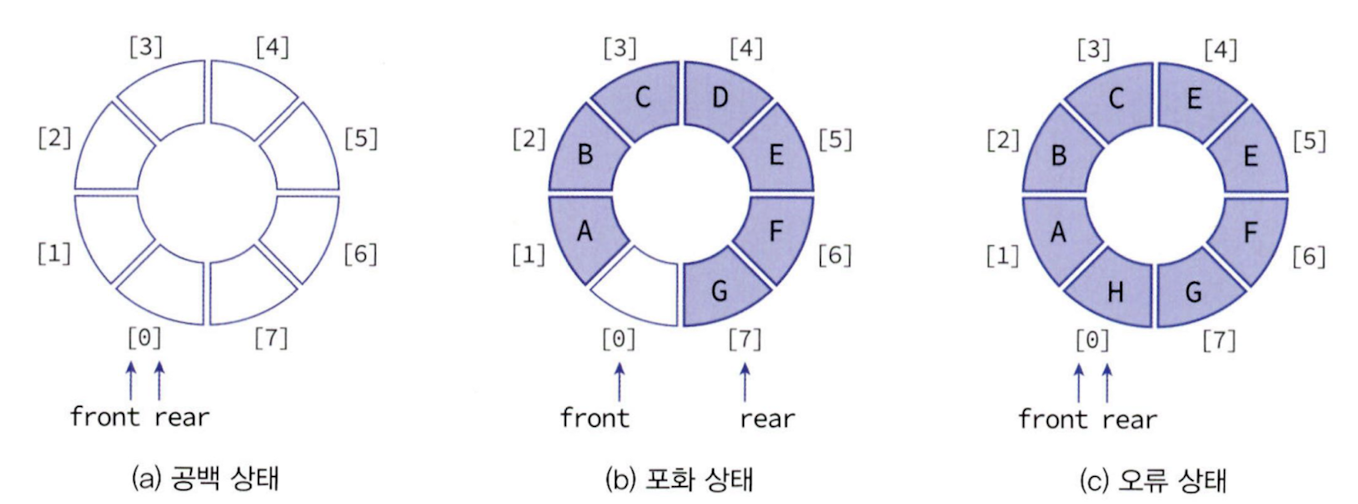
원형 큐가 포화 상태일 때 front가 0이고, rear이 7을 가리킨다. 이 때 그냥 +1을 해주면 존재하지 않는 인덱스인 8이 되는데 이를 최대 크기의 나머지를 구하면 인덱스 0에 접근할 수 있게 된다.
아래는 원형 큐를 활용한 레벨 순회 코드이다.
레벨 순회 구현
void level_order(TreeNode* ptr) {
QueueType q;
init_queue(&q);
if (ptr == NULL) return;
enqueue(&q, ptr);
while (!is_empty(&q)) {
ptr = dequeue(&q);
printf(" [%d] ", ptr->data);
if (ptr->left)
enqueue(&q, ptr->left);
if (ptr->right)
enqueue(&q, ptr->right);
}
}
TreeNode n1 = { 1, NULL, NULL };
TreeNode n2 = { 4, &n1, NULL };
TreeNode n3 = { 16, NULL, NULL };
TreeNode n4 = { 25, NULL, NULL };
TreeNode n5 = { 20, &n3, &n4 };
TreeNode n6 = { 15, &n2, &n5 };
TreeNode* root = &n6;
int main() {
printf("레벨 순회: ");
level_order(root);
printf("\n");
return 0;
}
// 출력
// 레벨 순회= [15] [4] [20] [1] [16] [25]출처
C언어로 쉽게 풀어쓴 자료구조 - 천인구
https://yoongrammer.tistory.com/68
https://monsieursongsong.tistory.com/6
https://velog.io/@kimdukbae/자료구조-트리-Tree
https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html