허프만 코딩
이진 트리는 각 글자의 빈도가 알려져 있는 메시지의 내용을 압축하는데 사용될 수 있다. 이런 특별한 종류의 이진트리를 허프만 코딩 트리라고 부른다.
빈도수를 구하는 이유는 가변 길이의 비트열을 사용하기 위함이다. 빈도수가 가장 많은 글자에는 짧은 비트열을 사용하고, 잘 사용하지 않아 빈도수가 적은 글자에는 긴 비트열을 사용하여 전체의 크기를 줄이는 것이다.
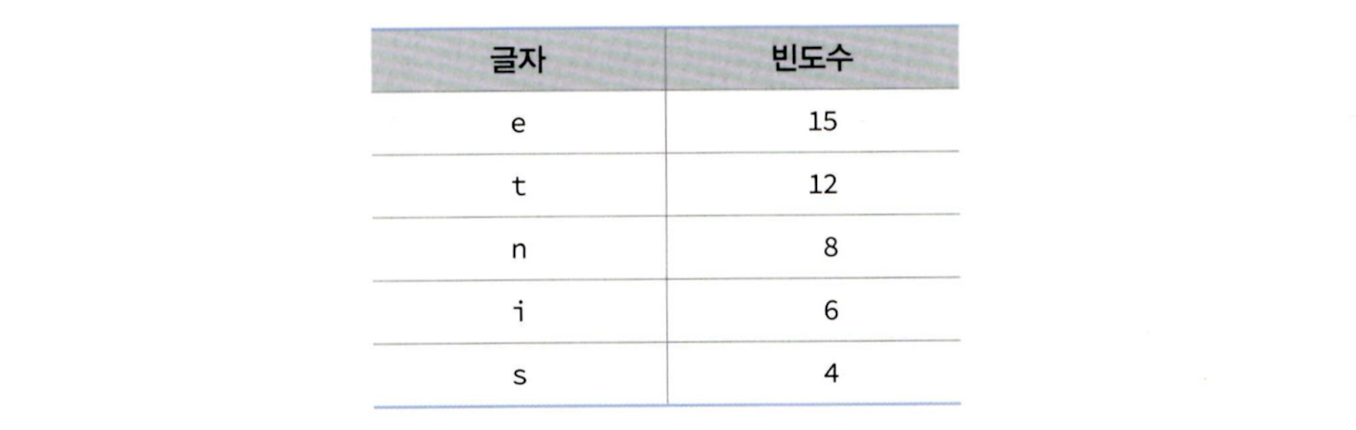
예를 들어 편지에서 알파벳의 빈도수를 테이블에 저장했다고 가정해 보자.
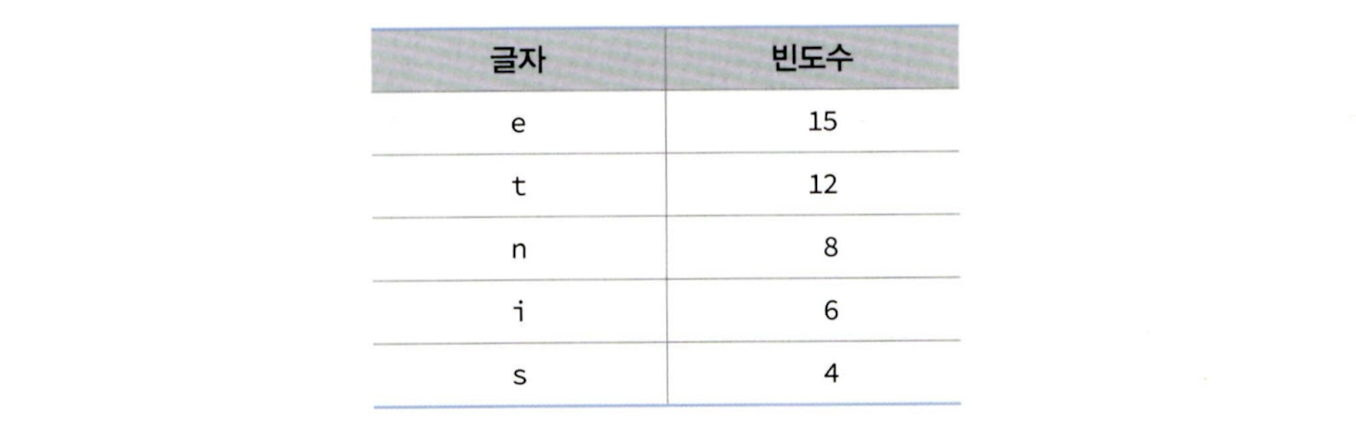
텍스트의 길이가 45글자이므로 한 글자를 3비트로 표시하는 아스키 코드의 경우, 45 x 3 = 135 비트가 필요하다. 그러나 만약 가변 길이의 코드를 만들어서 사용했을 경우에는 15 x 2 + 12 x 2 + 8 x 2 + 6 x 3 + 4 x 3 = 88 비트만 있으면 되므로 더 적은 비트로 표현될 수 있다.
그럼 해당 비트(코드)는 어떻게 설정되었는지 의문이 생길 수 있는데, 이 비트는 이진 트리를 통해 구할 수 있다.
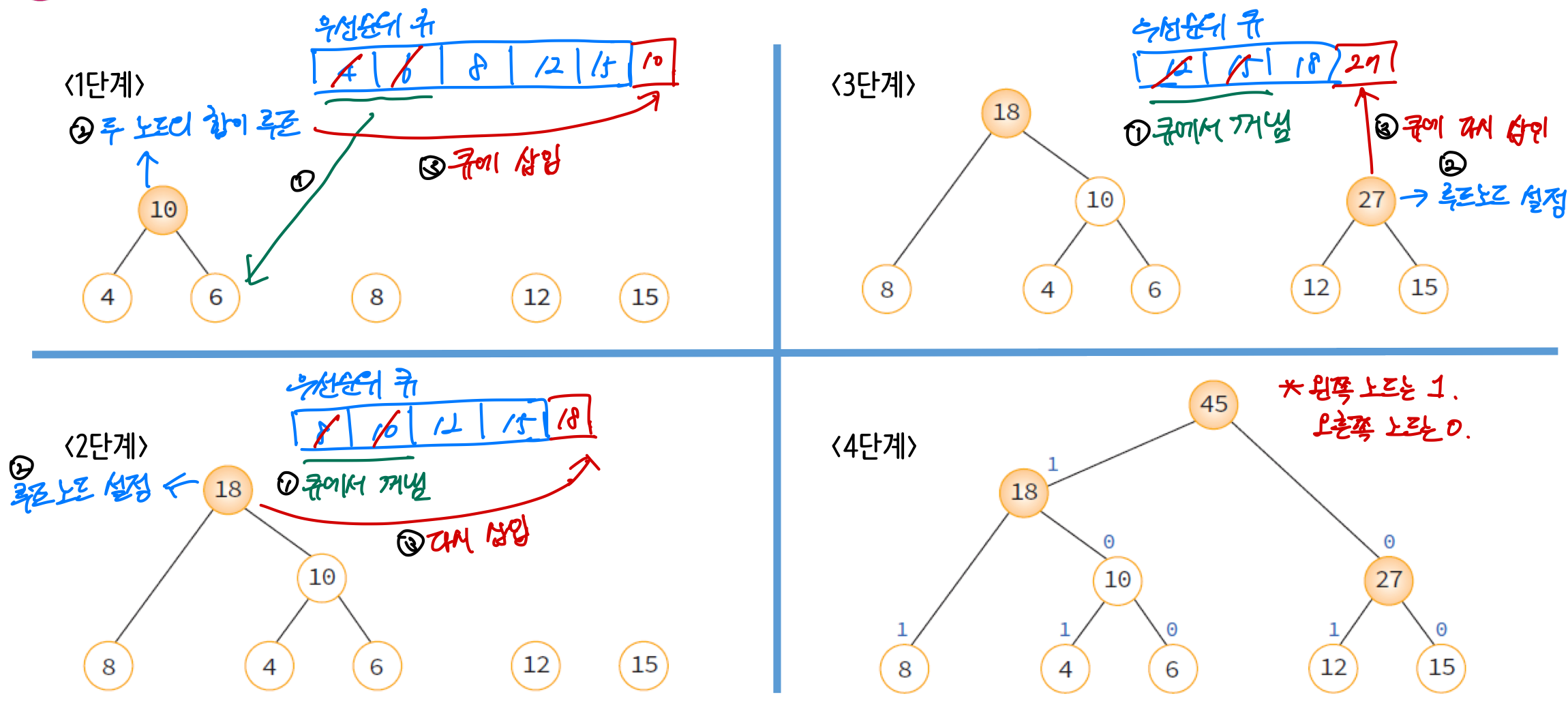
이진 트리를 통해 비트(코드)를 구하는 과정은 아래와 같다.
- 우선순위 큐에 각 문자의 빈도수를 넣어준다(최소 힙)
- 두 노드를 꺼내서 두 노드의의 합을 루트 노드로 설정
- 설정한 루트 노드를 우선순위 큐에 삽입
- 2~3번을 우선순위 큐가 모두 빌 때까지 계속 반복
- 완성된 허프만 이진 트리를 루트 노드를 기준으로 왼쪽은 1, 오른쪽은 0으로 설정
이런 과정을 통해 각 문자의 비트열이 구해진 것이다. 그럼 이제 코드로 구현해보자.
허프만 코드 구현
구조체 정의
typedef struct TreeNode {
int weight;
char ch;
struct TreeNode* left;
struct TreeNode* right;
} TreeNode;
typedef struct {
TreeNode* ptree;
char ch;
int key;
} element;
typedef struct {
element heap[MAX_ELEMENT];
int heap_size;
} HeapType;허프만 코드는 이진 트리로 구현하기 때문에 트리 노드를 정의해준다. 그리고 데이터를 담을 element라는 구조체를 정의해준다. 마지막으로 우선순위 큐로 사용할 HeapType을 정의해준다.
허프만 트리 생성
void huffman_tree(int freq[], char ch_list[], int n) {
int i;
TreeNode* node, * x;
HeapType* heap;
element e, e1, e2;
int codes[100];
int top = 0;
heap = create();
init(heap);
for (i = 0; i < n; i++) {
node = make_tree(NULL, NULL); // 이진 트리 생성
e.ch = node->ch = ch_list[i];
e.key = node->weight = freq[i];
e.ptree = node;
insert_min_heap(heap, e);
}
// 마지막 노드는 남겨놓기 위해 n-1 반복
for (i = 1; i < n; i++) {
e1 = delete_min_heap(heap);
e2 = delete_min_heap(heap);
x = make_tree(e1.ptree, e2.ptree);
e.key = x->weight = e1.key + e2.key;
e.ptree = x;
printf("%d+%d->%d \n", e1.key, e2.key, e.key);
insert_min_heap(heap, e);
}
e = delete_min_heap(heap);
print_codes(e.ptree, codes, top); // 비트(코드) 출력
destroy_tree(e.ptree);
free(heap);
}변수 선언한 부분을 보면 노드와 루트 노드(x)를 선언해주고, 비트열 코드를 저장할 배열을 만들어준다.
첫번째 반복문을 보면 이진 트리를 생성한 후 element와 node에 문자와 빈도수를 저장해준다. element에서는 빈도수를 key로 저장하고, node에서는 weight으로 저장한다. 이렇게 생성된 node를 element의 ptree에 저장하고 트리와 문자, 키를 포함한 element 전체를 최소 힙으로 우선순위 큐(배열)에 넣어준다.
두번째 반복문을 보면 우선순위 큐에 있는 첫번째 노드와 두번째 노드를 꺼내와 e1, e2에 저장한다. 그리고 루트 노드(x)를 e1.ptree와 e2.ptree를 연결하여 만들어주고, e1과 e2의 키의 합을 저장해준다. 마지막으로 루트 노드(x)를 e.ptree에 할당해주고 element 전체를 우선순위 큐에 다시 넣어준다.
정리해보며 첫번째 반복문에서는 각 element를 생성하여 우선순위 큐에 넣어주는 역할을 하고, 두번째 코드는 우선순위 큐에서 노드를 꺼내와 합친 후, 다시 우선순위 큐에 넣어주는 기능을 수행하고 있다.
이 과정이 모두 완료되면 비트(코드)를 출력 후 트리를 모두 소멸시키고 종료한다.
비트(코드) 출력
void print_codes(TreeNode* root, int codes[], int top) {
// 루트 노드의 다음 층부터 top이 0이라 생각하면 됨.
// 즉, 같은 층에 있는 노드의 코드는 해당 층의 배열에 저장됨.(배열의 인덱스가 층을 나타냄)
if (root->left) {
codes[top] = 1;
print_codes(root->left, codes, top + 1); // 다음 층으로 내려감
}
if (root->right) {
codes[top] = 0;
print_codes(root->right, codes, top + 1); // 다음 층으로 내려감
}
if (is_leaf(root)) {
printf("%c: ", root->ch);
print_array(codes, top);
}
}아래는 위 코드를 그림으로 나타낸 것이다.

top은 루트 노드를 제외한 각 층을 나타내며, codes 배열의 인덱스로 top을 사용하여 비트(코드)를 저장한다.
전체 코드
#include <stdio.h>
#include <stdlib.h>
#define MAX_ELEMENT 200
typedef struct TreeNode {
int weight;
char ch;
struct TreeNode* left;
struct TreeNode* right;
} TreeNode;
typedef struct {
TreeNode* ptree;
char ch;
int key;
} element;
typedef struct {
element heap[MAX_ELEMENT];
int heap_size;
} HeapType;
HeapType* create() {
return (HeapType*)malloc(sizeof(HeapType));
}
void init(HeapType* h) {
h->heap_size = 0;
}
void insert_min_heap(HeapType* h, element item) {
int i;
i = ++(h->heap_size);
while ((i != 1) && (item.key < h->heap[i / 2].key)) {
h->heap[i] = h->heap[i / 2];
i /= 2;
}
h->heap[i] = item;
}
element delete_min_heap(HeapType* h) {
int parent, child;
element item, temp;
item = h->heap[1];
temp = h->heap[(h->heap_size)--];
parent = 1;
child = 2;
while (child <= h->heap_size) {
if (child < h->heap_size
&& (h->heap[child].key > h->heap[child + 1].key)) {
child++;
}
if (temp.key < h->heap[parent].key) break;
h->heap[parent] = h->heap[child];
parent = child;
child *= 2;
}
h->heap[parent] = temp;
return item;
}
TreeNode* make_tree(TreeNode* left, TreeNode* right) {
TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
node->left = left;
node->right = right;
return node;
}
void destroy_tree(TreeNode* root) {
if (root == NULL) return;
destroy_tree(root->left);
destroy_tree(root->right);
free(root);
}
int is_leaf(TreeNode* root) {
return !(root->left) && !(root->right);
}
void print_array(int codes[], int n) {
for (int i = 0; i < n; i++)
printf("%d", codes[i]);
printf("\n");
}
void print_codes(TreeNode* root, int codes[], int top) {
// 루트 노드의 다음 층부터 top이 0이라 생각하면 됨.
// 즉, 같은 층에 있는 노드의 코드는 해당 층의 배열에 저장됨.(배열의 인덱스가 층을 나타냄)
if (root->left) {
codes[top] = 1;
print_codes(root->left, codes, top + 1); // 다음 층으로 내려감
}
if (root->right) {
codes[top] = 0;
print_codes(root->right, codes, top + 1); // 다음 층으로 내려감
}
if (is_leaf(root)) {
printf("%c: ", root->ch);
print_array(codes, top);
}
}
void huffman_tree(int freq[], char ch_list[], int n) {
int i;
TreeNode* node, * x;
HeapType* heap;
element e, e1, e2;
int codes[100];
int top = 0;
heap = create();
init(heap);
for (i = 0; i < n; i++) {
node = make_tree(NULL, NULL);
e.ch = node->ch = ch_list[i];
e.key = node->weight = freq[i];
e.ptree = node;
insert_min_heap(heap, e);
}
// 마지막 노드는 남겨놓기 위해 n-1 반복
for (i = 1; i < n; i++) {
e1 = delete_min_heap(heap);
e2 = delete_min_heap(heap);
x = make_tree(e1.ptree, e2.ptree);
e.key = x->weight = e1.key + e2.key;
e.ptree = x;
printf("%d+%d->%d \n", e1.key, e2.key, e.key);
insert_min_heap(heap, e);
}
e = delete_min_heap(heap);
print_codes(e.ptree, codes, top);
destroy_tree(e.ptree);
free(heap);
}
int main() {
char ch_list[] = { 's', 'i','n','t','e' };
int freq[] = { 4, 6, 8, 12, 15 };
huffman_tree(freq, ch_list, 5);
return 0;
}출처
C언어로 쉽게 풀어쓴 자료구조 - 천인구
