깊이 우선 탐색(DFS: Depth first search)

DFS는 트리에서 이해하면 쉽다.(트리도 그래프의 일종이기 때문) 트리를 탐색할 때 시작 정점에서 한 방향으로 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 다른 방향으로 다시 탐색을 진행하는 방법과 유사하다.

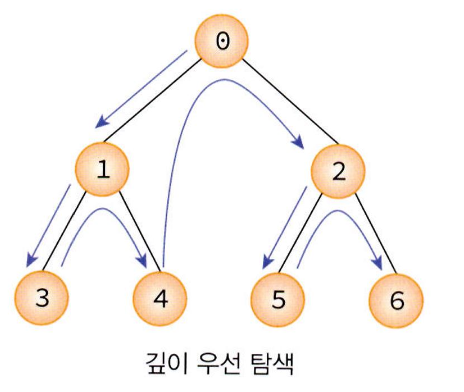
위 그림에서 탐색 순서는 0→1→3→4→2→5→6의 순서대로 탐색이 진행된다.

좀 더 자세히 설명해 보면 한 방향으로 갈 수 있을 때까지 가다가 더 이상 갈 수 없게 되면 가장 가까운 갈림길로 돌아와서 이 곳으로부터 다른 방향으로 다시 탐색을 진행한다.

되돌아가기 위해서는 스택을 활용하고, 재귀 함수를 사용해서 묵시적인 스택 형태로 사용해도 된다.

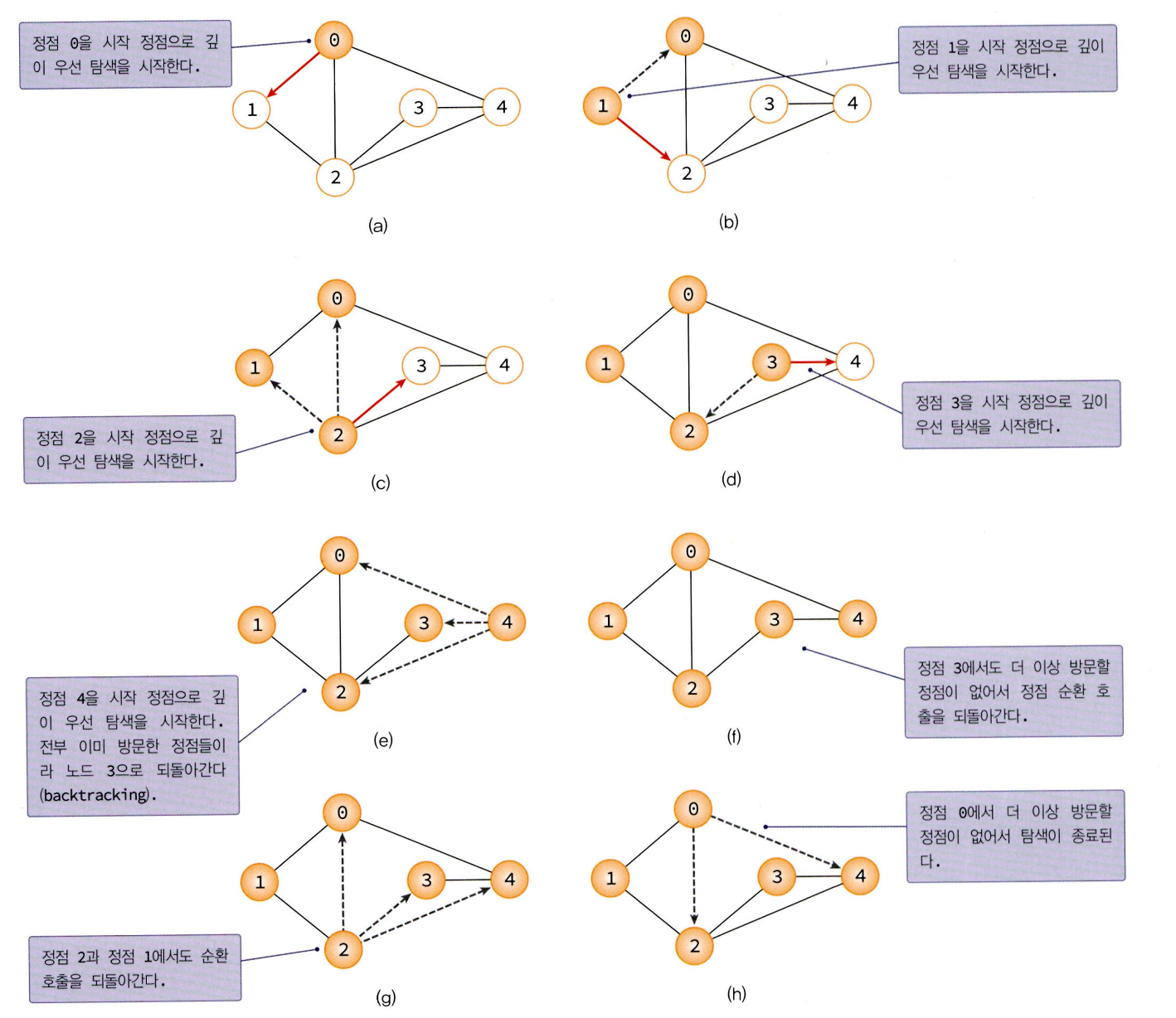
깊이 우선 탐색을 구현하는 방법에는 인접 행렬과 리스트 두 가지가 있다.

인접 행렬로 작성한 코드

#include <stdio.h>
#include <stdlib.h>

#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 50

typedef struct GraphType {
	int n;
	int adj_mat[MAX_VERTICES][MAX_VERTICES];
} GraphType;

int visisted[MAX_VERTICES];

void init(GraphType* g) {
	int r, c;
	g->n = 0;
	for (r = 0; r < MAX_VERTICES; r++)
		for (c = 0; c < MAX_VERTICES; c++)
			g->adj_mat[r][c] = 0;
}

void insert_vertex(GraphType* g, int v) {
	g->n++; // 인접 행렬의 크기가 정점의 개수
}

void insert_edge(GraphType* g, int start, int end) {
	g->adj_mat[start][end] = 1;
	g->adj_mat[end][start] = 1;
}

void dfs_mat(GraphType* g, int v) {
	int w;
	visisted[v] = TRUE;

	printf("정점 %d -> ", v);
	for (w = 0; w < g->n; w++) {
		// 간선이 존재하고, 방문하지 않은 노드라면 재귀함수 실행
		if (g->adj_mat[v][w] && !visisted[w])
			dfs_mat(g, w);
	}
}

int main() {
	GraphType* g;
	g = (GraphType*)malloc(sizeof(GraphType));
	init(g);
	for (int i = 0; i < 4; i++) {
		insert_vertex(g, i);
	}

	insert_edge(g, 0, 1);
	insert_edge(g, 0, 2);
	insert_edge(g, 0, 3);
	insert_edge(g, 1, 2);
	insert_edge(g, 2, 3);

	printf("깊이 우선 탐색\n");
	dfs_mat(g, 0);
	printf("\n");

	free(g);

	return 0;
}

인접 리스트로 구현

#include <stdio.h>
#include <stdlib.h>

#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 50

typedef struct GraphNode {
	int vertex;
	GraphNode* link;
};

typedef struct GraphType {
	int n;
	GraphNode* adj_mat[MAX_VERTICES];
} GraphType;

int visisted[MAX_VERTICES];

void init(GraphType* g) {
	g->n = 0;
	for (int i = 0; i < MAX_VERTICES; i++)
		g->adj_mat[i] = NULL;
}

void insert_vertex(GraphType* g, int v) {
	g->n++; // n개의 리스트 그룹 생성
}

void insert_edge(GraphType* g, int u, int v) {
	GraphNode* node = (GraphNode*)malloc(sizeof(GraphNode));
	node->vertex = v;
	node->link = g->adj_mat[u];
	g->adj_mat[u] = node;
}

void dfs_list(GraphType* g, int v) {
	GraphNode* w;
	visisted[v] = TRUE;

	printf("정점 %d ->", v);
	for (w = g->adj_mat[v]; w; w = w->link) {
		if (!visisted[w->vertex])
			dfs_list(g, w->vertex);
	}
}

int main() {
	GraphType* g;
	g = (GraphType*)malloc(sizeof(GraphType));
	init(g);
	for (int i = 0; i < 4; i++) {
		insert_vertex(g, i);
	}

	insert_edge(g, 0, 1);
	insert_edge(g, 0, 2);
	insert_edge(g, 0, 3);
	insert_edge(g, 1, 2);
	insert_edge(g, 2, 3);

	printf("깊이 우선 탐색\n");
	dfs_list(g, 0);
	printf("\n");

	free(g);

	return 0;
}

깊이 우선 탐색(DFS)의 분석

깊이 우선 탐색의 시간 복잡도는 다음과 같다.

• 시간 복잡도가 인접 리스트는 O(n + e)이다. 왜냐하면 각 노드를 처음에 배열로 저장(n)하고, 각 배열에 연결된 리스트(간선(e))를 순차적으로 탐색하는 구조이기 때문이다.
• 인접 행렬은 O(n^2)가 된다. 2차원 배열로 저장했기 때문이다.

출처
C언어로 쉽게 풀어쓴 자료구조 - 천인구