[알고리즘] 외판원 순회 문제

leeeha·2022년 7월 17일

알고리즘

목록 보기

14/20

참고 자료

https://loosie.tistory.com/272#

https://velog.io/@ja_an/이산수학-오일러-순환과-해밀턴-순환

해밀턴 순환이란?

해밀턴 경로: 그래프 G의 모든 정점(vertex)을 딱 한번씩만 지나는 경로
해밀턴 순환: 시작점과 끝점이 같은 해밀턴 경로! 즉, 그래프의 모든 정점을 딱 한번씩만 지나면서 시작점과 끝점이 같은 경로를 해밀턴 순환이라고 한다.
- 브루트포스로 $O(x^n)$ 의 지수 시간이 걸림. (x: 간선 개수, n: 정점 개수)
- 해밀턴 순환 문제를 다항시간 안에 푸는 알고리즘은 아직 발견되지 않아서 NP 문제에 속함.

📌 P-NP 문제가 무엇인지 잠깐! 알아보자! (~~토글로 넣고 싶었는데 미리보기에서는 되지만, 게시글에는 적용이 안 된다,,,,)~~

‘P’는 컴퓨터가 쉽게 해결할 수 있는 문제를 말한다.
‘NP’는 직소 퍼즐이나 스도쿠처럼 한번 해결하면 검산하기 쉬운 문제를 뜻한다. 많은 NP 문제들은 사회가 직면한 가장 고질적이고 긴급한 문제에 해당한다.

P 대 NP로 제기되는 100만달러짜리 질문이란 다음과 같다. P 집합과 NP 집합은 동일한 하나의 집합일까? 다시 말해, 어려워 보이는 문제들을 일정 시간 안에 알고리즘을 통해 해결할 수 있을까? 만약 엄청나게 빠르고 탁월한 알고리즘만 있다면 말이다. 실제로 그렇다면 수많은 어려운 문제들이 갑자기 해결된다. 그리고 이 알고리즘 해법들은 의학과 공학, 경제학, 생물학, 생태학, 신경과학, 사회과학, 산업, 예술, 심지어 정치 및 그 밖의 분야에 유토피아적인 사회 혁신을 가져올 수 있다.

때로 이 분류에 변화가 생기기도 한다. 전에는 어려웠던 문제가 연구자들이 더 효율적인 해법을 발견함으로써 쉬운 문제가 되는 것이다. 예를 들어, 어떤 숫자가 소수(prime)인지 여부를 시험하는 것은 1970년대 중반부터 NP 집합에 속하는 것으로 알려져 왔다. 그러나 2002년 인도 공과대학교 칸푸르(Indian Institute of Technology Kanpur)의 세 컴퓨터 과학자가 증명과 알고리즘을 고안함으로써, 이 문제가 P 집합임이 마침내 확인되었다.

만일 모든 까다로운 문제가 이러한 알고리즘적 기법을 통해 P 문제로 전환될 수 있다면, 그 결과는 인류와 지구에 엄청난 영향을 끼칠 것이다.

우선 NP 문제에 기반한 대부분의 암호화 시스템이 무력화될 것이다. 기밀 통신에는 완전히 다른 접근법이 필요해지게 된다. 지난 50년 간 생물학계의 가장 큰 도전이었던 단백질 접힘 문제도 풀기 수월해져, 질병 치료 목적으로 약을 설계하거나 산업 폐기물 분해용 효소를 개발할 수 있게 될 것이다. 또한 여러 목적지를 들르기 위한 최단 거리를 계획하거나, 지인끼리 동석하게 결혼식 하객석을 배치하는 것과 같은 일상적인 문제에도 최적의 해결책을 찾을 수 있게 된다.

더 자세한 설명 참고: 수학 7대 난제 P-NP 문제

TSP (Traveling Salesman Problem, 외판원 순회 문제)

요약

간선에 비용이 주어지며, 일반적으로 완전 그래프이다.
이 그래프에서 비용이 최소가 되는 해밀톤 순환을 찾는 문제
- n≤11일 경우: 브루트포스(O(n!))
- n≤12일 경우: 백트래킹
- n≤16일 경우: DP + BitMasking ( $n^2 * 2^n$ )

소개

TSP (Travelling Salesman Problem, 일명 외판원 순회 문제)는 조합 최적화(Combinatorial Optimization) 문제로 전산학에서 연구된 가장 유명한 문제 중 하나다.

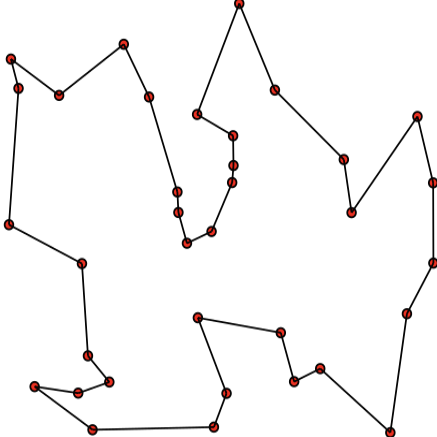
여러 도시들이 있고 한 도시에서 다른 도시로 이동하는 비용이 모두 주어졌을 때, 모든 도시들을 단 한 번만 방문하고 원래 시작점으로 돌아오는 최소 비용의 이동 순서를 구하는 것이다. 그래프 이론의 용어로 엄밀하게 정의한다면, "각 변에 가중치가 주어진 완전 그래프(weighted complete graph)에서 가장 작은 가중치를 가지는 해밀턴 순환을 구하라"라고 표현할 수 있다. 이 문제는 반드시 시작점으로 돌아와야 한다는 제약 조건을 없애도 계산 복잡도는 변하지 않는다.

외판원 순회 알고리즘은 브루트포스로 무식하게 풀 수 있다. 무조건 0번 도시에서 출발한다고 가정해도 경로의 길이는 다르지 않다. 그러면 남은 도시들을 어떤 순서로 방문할지를 정하기만 하면 된다. 남은 n-1개의 도시를 나열하는 방법으로는 (n-1)!가지가 있다. 그래서 재귀 호출을 통해 쉽게 외판원 순회 알고리즘을 설계할 수 있다. 그러나 보통 n!의 풀이는 사용하지 않는다. 12!만 해도 479,001,600라는 엄청난 수를 지니기 때문이다.

DP와 비트마스킹

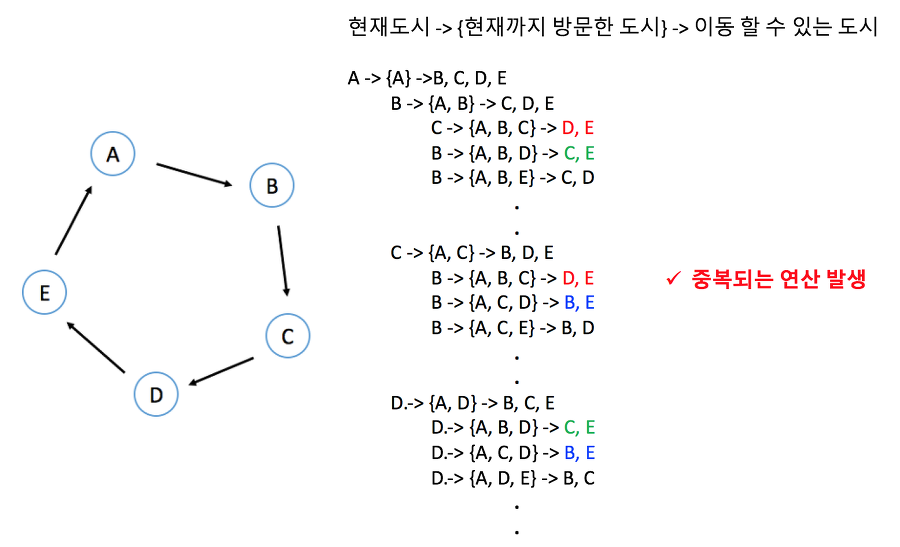
출발 정점을 제외하고 모든 정점을 한번씩 방문하는 최단 순환 경로를 효율적으로 구하려면 어떻게 해야 할까?

(n-1)!의 모든 경로를 조사하지 않고, 중복된 경로를 제거하는 DP 메모이제이션 기법을 사용하면 된다. 동일한 하위 문제의 반복을 막아줌으로써 더 높은 효율로 연산이 이루어지게 해준다. 중복되는 경로의 조사를 제거해주는 것이다.

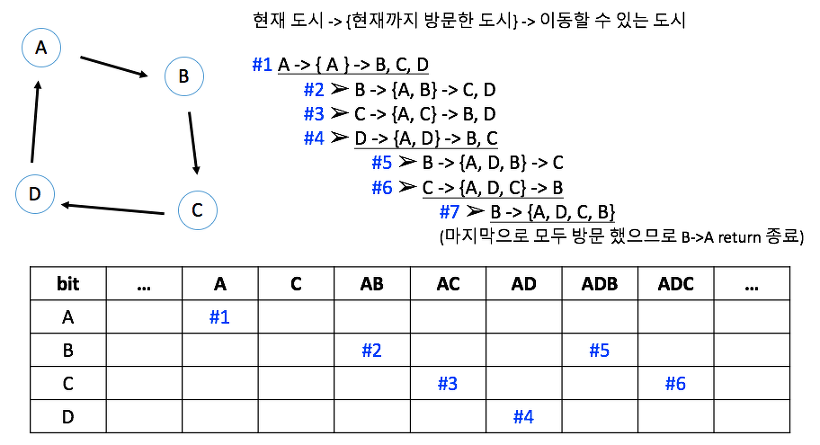
그리고 비트마스킹을 사용하면 bit 연산이기 때문에 다른 자료구조를 사용하는 것보다 훨씬 빠르게 동작하고 코드도 간결해진다. 왜냐하면 예를 들어 n이 16개인 경우 2^16가지의 경우를 16bit로 표현할 수 있기 때문이다. (ex. 16개의 지점 중 1, 3, 4, 5번 지점 방문 → 0000 0000 0001 1101)

정리하면, 외판원 순회 문제는 한 도시에서 다른 도시로 이동하는 비용이 모두 주어졌을 때, 모든 도시들을 단 한번씩만 방문하고 원래 시작점으로 돌아오는 최소 비용을 구하는 문제인데,

그때 1) n!의 중복 경로를 제거해주는 DP 메모이제이션 기법을 사용한다. 그래도 2^n의 모든 경우의 수를 표현해야 하기 때문에 그만큼의 공간복잡도가 필요하다.

그래서 2) 메모리 사용량도 줄이고 성능 향상을 위해 2^n의 경우의 수를 n bit로 표현할 수 있는 비트마스킹을 사용한다.

즉, 최적화 접근 방식으로 DP 메모이제이션과 비트마스킹을 사용하여 올라가야 할 계단의 수를 100에서 1로 줄이는 설계 방법이라고 볼 수 있다.

한 정점만 탐색해도 되는 이유

DP 메모이제이션 기법으로 엄청나게 시간을 단축할 수 있는 건 그만큼 중복되는 경로가 많기 때문이다. 외판원 순회 문제는 한 정점에서 다른 모든 정점을 순회하여 다시 출발 정점으로 돌아오는 최적의 경로를 찾는 알고리즘이다. 이 순회 경로는 n개의 정점 중에 어느 정점에서 탐색을 시작해도 결과가 똑같다.

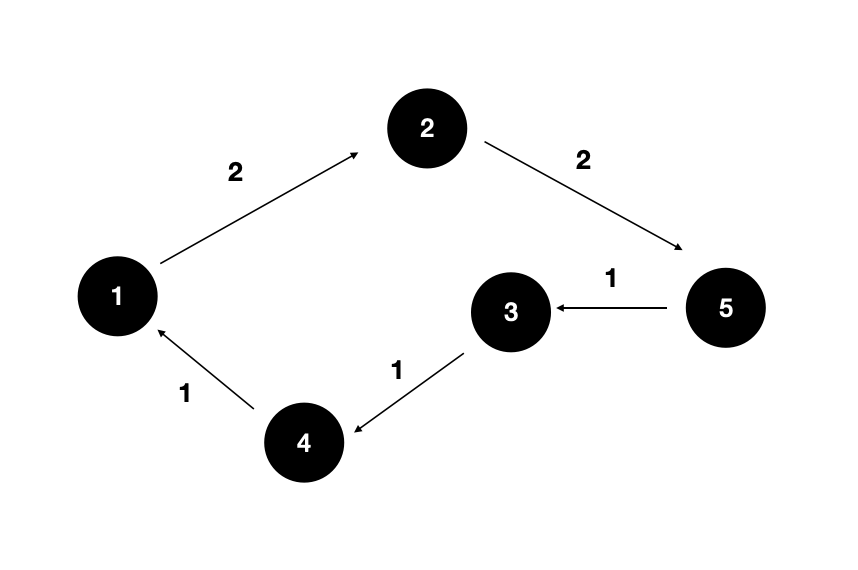
1, 2, 3, 4, 5번 어느 정점에서 출발하든 최적의 순회 경로는 동일하다. 따라서 한 정점에서만 탐색해줘도 된다.

백준 2098번

문제

https://www.acmicpc.net/problem/2098

외판원 순회 문제는 영어로 Traveling Salesman Problem (TSP) 라고 불리는 문제로 computer science 분야에서 가장 중요하게 취급되는 문제 중 하나이다. 여러 가지 변종 문제가 있으나, 여기서는 가장 일반적인 형태의 문제를 살펴보자.

1번부터 N번까지 번호가 매겨져 있는 도시들이 있고, 도시들 사이에는 길이 있다. (길이 없을 수도 있다) 이제 한 외판원이 어느 한 도시에서 출발해 N개의 도시를 모두 거쳐 다시 원래의 도시로 돌아오는 순회 여행 경로를 계획하려고 한다. 단, 한 번 갔던 도시로는 다시 갈 수 없다. (맨 마지막에 여행을 출발했던 도시로 돌아오는 것은 예외) 이런 여행 경로는 여러 가지가 있을 수 있는데, 가장 적은 비용을 들이는 여행 계획을 세우고자 한다.

각 도시 간에 이동하는데 드는 비용은 행렬 W[i][j] 형태로 주어진다. W[i][j]는 도시 i에서 도시 j로 가기 위한 비용을 나타낸다. 비용은 대칭적이지 않다. 즉, W[i][j] 는 W[j][i]와 다를 수 있다. 모든 도시 간의 비용은 양의 정수이다. W[i][i]는 항상 0이다. 경우에 따라서 도시 i에서 도시 j로 갈 수 없는 경우도 있으며 이럴 경우 W[i][j]=0이라고 하자.

N과 비용 행렬이 주어졌을 때, 가장 적은 비용을 들이는 외판원의 순회 여행 경로를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 도시의 수 N이 주어진다. (2 ≤ N ≤ 16) 다음 N개의 줄에는 비용 행렬이 주어진다. 각 행렬의 성분은 1,000,000 이하의 양의 정수이며, 갈 수 없는 경우는 0이 주어진다. W[i][j]는 도시 i에서 j로 가기 위한 비용을 나타낸다.

항상 순회할 수 있는 경우만 입력으로 주어진다.

출력

첫째 줄에 외판원의 순회에 필요한 최소 비용을 출력한다.

예제

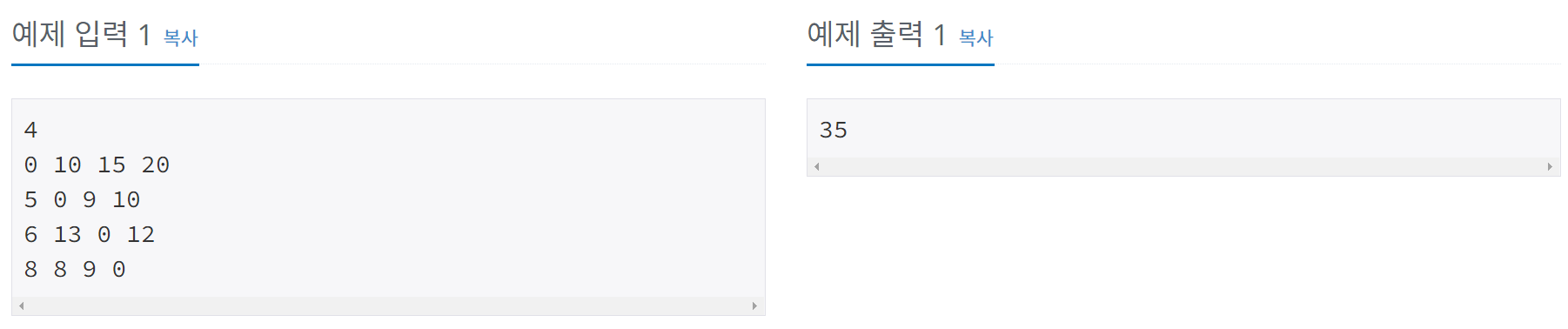
풀이 (C++)

참고 자료
https://withhamit.tistory.com/246
https://yabmoons.tistory.com/358
https://red-pulse.tistory.com/29

모든 노드를 순회하는 최적의 경로는 브루트포스로 해결 가능하지만 노드 개수가 10개를 넘어가면 시간초과가 발생한다. 이 문제는 최대 16개의 노드이기 때문에 dp의 메모이제이션 기법을 사용해야 한다.

int dp[16][1 << 16] // 현재 노드 번호와 이제까지의 방문 상태를 저장하는 dp 테이블

그리고 최소 순회 경로를 찾게 된다면 모두 같은 경로이기 때문에, 모든 노드에 대한 탐색 경로를 찾을 필요 없이, 한 노드에 대한 최소 순회 경로만 찾으면 된다!

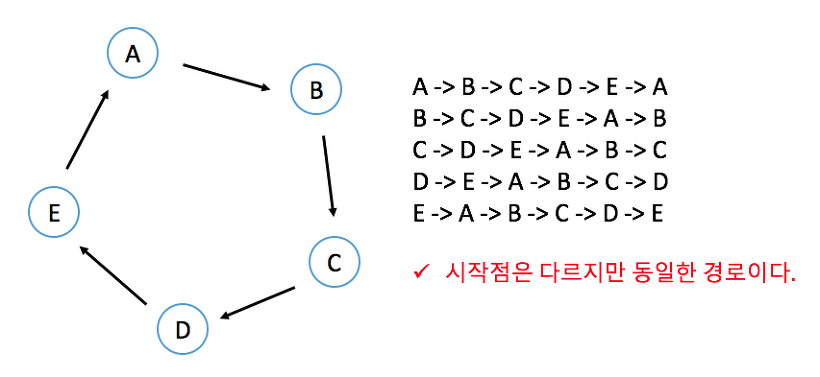
#include <iostream>
#define INF 1e9 
using namespace std; 

int N, END;
int cost[16][16];
int dp[16][1 << 16]; 

int TSP(int now, int visited){
	// 모든 노드를 방문했는데 
	if(visited == END){
		// 현재 노드에서 0번으로 가는 경로가 있으면 
		if(cost[now][0] > 0){ 
			return cost[now][0]; // 최소 비용 반환 
		}

		return INF; // 불가능한 경우에는 INF 반환 
	}

	// 현재 상태를 이미 계산한 값이 dp 테이블에 있다면 그대로 사용
	if(dp[now][visited] != 0) return dp[now][visited];

	// 없으면 현재 노드에 대한 탐색 진행 
	dp[now][visited] = INF; 
    
	for(int i = 0; i < N; i++){
		// 현재 노드에서 i번 노드로 가는 경로가 없으면 패스
		if(cost[now][i] == 0) continue;
        
		// 이미 방문한 노드면 패스 
		if(visited & (1 << i)) continue;

		// i번 노드 방문 처리 후 최소 비용 반환 
		int temp = TSP(i, visited | 1 << i); 
		dp[now][visited] = min(dp[now][visited], cost[now][i] + temp); 
	}

	return dp[now][visited]; // 최소 비용 반환 
}

int main()
{ 
	ios::sync_with_stdio(0);
    cin.tie(0);

	cin >> N;
	END = (1 << N) - 1;

	for(int i = 0; i < N; i++){
		for(int j = 0; j < N; j++){
			cin >> cost[i][j]; 
		}
	}
	
	// 0번 노드부터 그래프 탐색 
	cout << TSP(0, 1) << "\n"; 

	return 0;
}