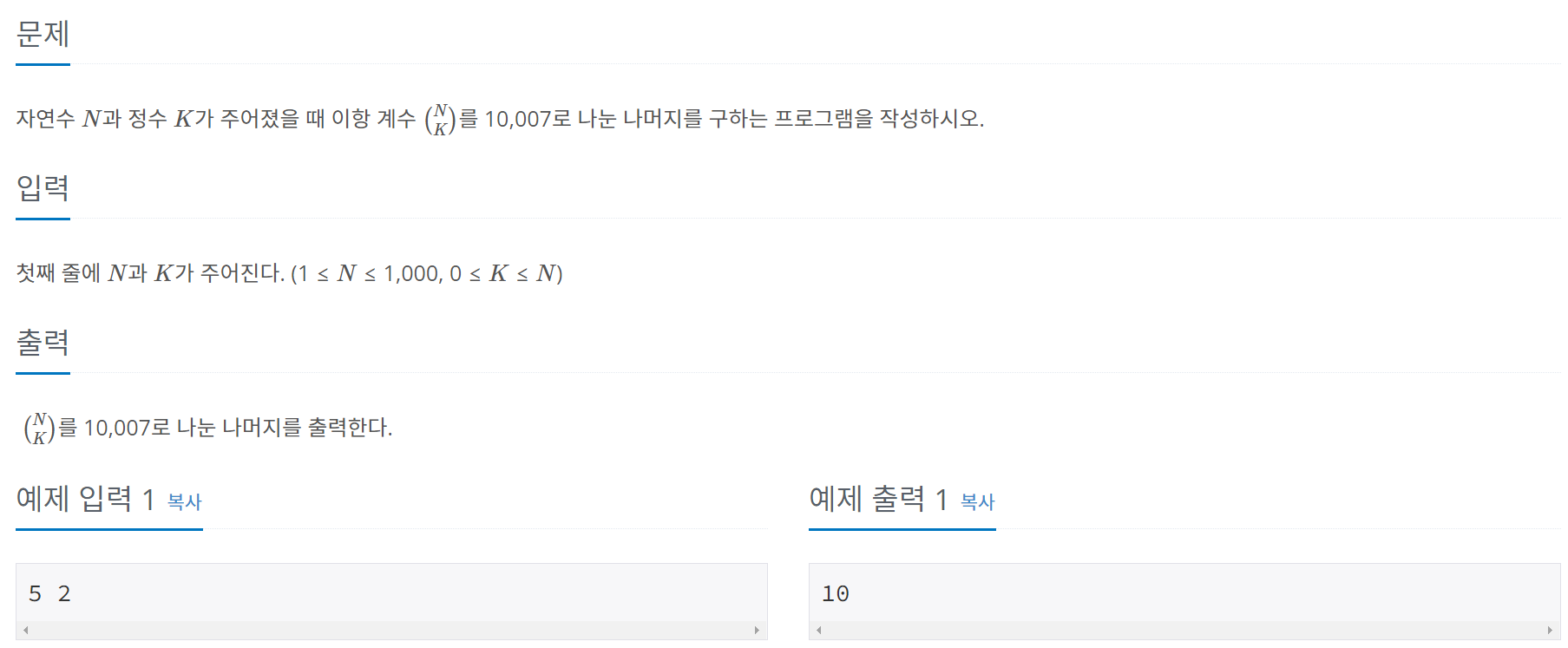
문제

https://www.acmicpc.net/problem/11051

---

풀이

https://rh-tn.tistory.com/32
https://camelsource.tistory.com/12

int binomial(int n, int r) {
	if(r == 0 || r == n) 
		return 1;
        
	return binomial(n - 1, r - 1) + binomial(n - 1, r);
}

이렇게 재귀호출로 풀면, 이항계수를 구하는 점화식에 따라 시간복잡도가 O(n!)이어서 시간초과가 발생한다.

이항계수를 구하는 점화식을 보면, 중복되는 부분 문제와 최적 부분 구조가 성립하므로, 쉽게 말해 작은 문제들의 해를 모아 큰 문제의 해를 구할 수 있으므로, 다이나믹 프로그래밍을 적용할 수 있다!

#include <iostream>
#include <vector>
#include <algorithm> 
using namespace std;

int dp[1001][1001]; 

int main()
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);

	int n, k;
	cin >> n >> k;

	// 1 <= n <= 1000, 0 <= k <= n 
	for(int i = 1; i <= n; i++){
		for(int j = 0; j <= n; j++){
			if(i == j || j == 0){
				dp[i][j] = 1;
			}else{
				dp[i][j] = (dp[i-1][j] + dp[i-1][j-1]) % 10007; 
			}
		}
	}

	cout << dp[n][k];

	return 0;
}

이렇게 풀면 시간복잡도 O(n^2)으로 문제를 해결할 수 있다.