
서론
게임에서 회전은 게임을 바라보는 시점에서나 탄환이 발사되는 방향 등을 결정하기 위해서 사용되며 매우 중요하다. 따라서 회전에 대한 자세한 이해가 필요하며 밑바탕에는 이를 지탱하는 수학이 필요하다.
오일러 각의 이해
오일러 각
오일러 각은 3차원 공간에서 물체가 놓인 방향을 3개의 각을 사용해 표시하는 방법이다.
오일러 각은 직관적이기 때문에 3차원 공간을 사용하는 프로그램에서는 자주 사용된다.
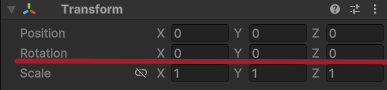
게임 엔진에서 오일러 각을 사용해 물체의 방향을 표시할 때는 표준기저벡터를 사용한다.
그래서 오일러 각은 표준기저벡터를 중심으로 회전하는 각의 크기를 지정된다.
또한, 각의 값은 실수이기 때문에 유니티에서 Vector3를 사용하여 관리할 수도 있다.
요, 롤, 피치
하지만 이렇게 구성된 오일러 각을 3D 공간을 사용하는 모든 프로그램에 범용적으로 적용하기에는 무리가 있다. 왜냐하면 프로그램마다 사용하는 좌표계가 모두 다르기 때문이다.
따라서 이런 문제를 해결하기 위해 x, y, z 축 대신 회전의 움직임으로 회전 동작을 구분하고 각을 지정하는 방법을 사용하다.
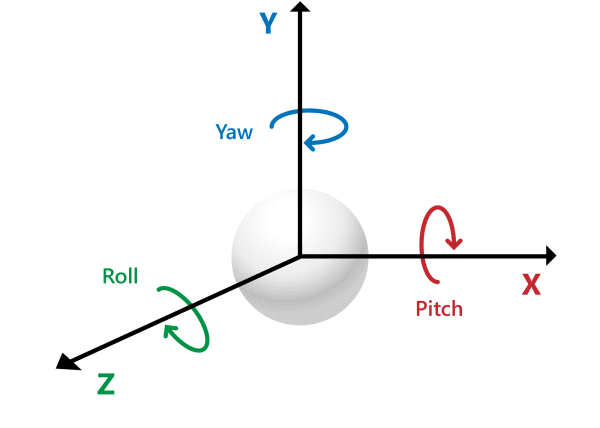
표준기저벡터를 축으로 하는 회전의 움직임은 방향에 따라 요(Yaw), 롤(Roll), 피치(Pitch)로 불린다.
오일러 각의 문제점
짐벌락
요, 롤, 피치를 이용하여 구성할 수 있는 회전 동작 순서의 모든 경우의 수는 다음과 같다.
| 경우 | 회전 축의 순서 | 회전 동작의 순서 |
|---|---|---|
| 1 | x → y → z | 피치 → 요 → 롤 |
| 2 | x → z → y | 피치 → 롤 → 요 |
| 3 | y → x → z | 요 → 피치 → 롤 |
| 4 | y → z → x | 요 → 롤 → 피치 |
| 5 | z → x → y | 롤 → 피치 → 요 |
| 6 | z → y → x | 롤 → 요 → 피치 |
유니티에서 채택한 방식은 5번 경우의 수다.
즉, z → x → y 순서로 회전을 하게 되며 다음과 같은 종속 관계를 가진다.
1. z축의 회전은 x, y축에도 영향을 미친다.
2. x축의 회전은 y축에 영향을 미친다.
3. y축의 회전은 영향이 없다.
여기서, x → y 회전을 하는 도중에 z축과 y축이 겹쳐버려서 z축과 y축의 회전이 동일해지면 한 축의 회전이 사라지는 꼴이 된다. 이를 짐벌락이라고 한다.
회전 보간
오일러 각에서 각 축 별로 선형 보간을 한다고 해서 실제 물체의 회전이 그 사이를 자연스럽게 지나가지 않는다.
회전은 선형 공간이 아닌 곡면 공간에서 일어나며, 오일러 각에서의 회전 보간은 이 공간을 따르지 않는다. 따라서 실제 회전은 왜곡되고 꼬인 경로로 보간된다.
또한 오일러 각에서는 와 같이 같은 회전을 여러 방법으로 표현할 수 있다. 선형 보간 과정에서 두 값 사이를 거칠 때는 이상한 회전이 발생할 수 있다.
