[BDA 데이터분석모델링반(ML1)] 2주차 교차검증

YJ·2024년 9월 22일

BDA python sklearn 데이터 분석 머신러닝

BDA 데이터분석모델링반(ML1)

목록 보기

2/7

교차검증

train/test/split으로 데이터를 나눈다.
데이터를 나누는 이유는?
- 일반화, 과적합을 막기 위함
- 평가지표가 train, validation, test에 따라 다르다.
  - 이때 지표에 대한 해석이 중요하다.
- train ≥ test이면서 차이가 최소화되는 것이 가장 이상적이다.

실습

iris 데이터 불러오기

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np
from sklearn.metrics import accuracy_score

# iris 데이터로 진행
iris = load_iris()
iris_data = iris.data
iris_label = iris.target
iris_df = pd.DataFrame(data=iris.data, columns= iris.feature_names)

## 데이터셋 정의
iris_df['y'] = iris_label

Train, Test 데이터로만 분리

# train_test_split 분류
X_train, X_test, y_train, y_test = train_test_split(iris_data, iris_label, test_size=0.3, random_state=111)

dt_clf = DecisionTreeClassifier(random_state=111)

dt_clf.fit(X_train, y_train) # train 데이터로 학습

train_pred = dt_clf.predict(X_train)
test_pred = dt_clf.predict(X_test)

print(accuracy_score(train_pred, y_train))
print(accuracy_score(test_pred, y_test))


# 실행 결과
1.0
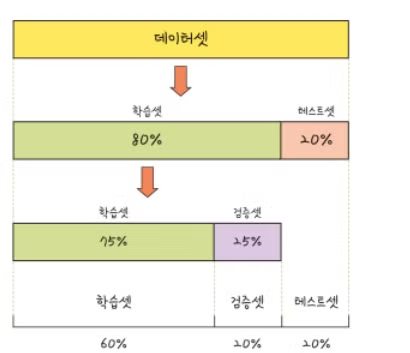
0.9333333333333333

Train, Validation, Test 데이터로 분리

과적합이나 성능을 더 정확히 측정하기 위함

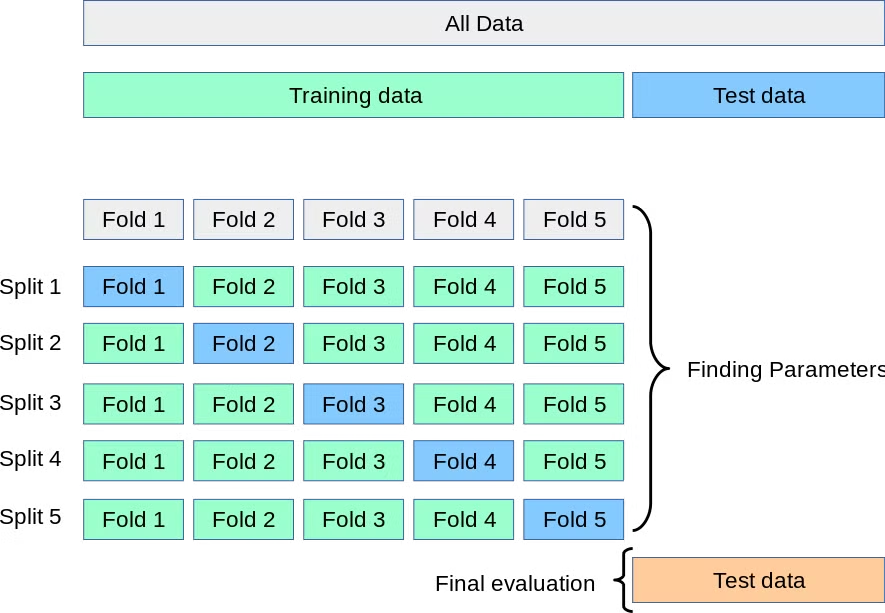
KFold 교차검증

데이터를 여러 개의 부분(폴드)으로 나누어 모델의 성능을 평가하는 방법

from sklearn.model_selection import KFold
kfold = KFold(n_splits=5)

cv_acc_train=[]
cv_acc_test=[]
kf_ml = DecisionTreeClassifier(random_state=111)

n_iter = 0

for train_idx, test_idx in kfold.split(iris_data):
    X_train, X_test = iris_data[train_idx], iris_data[test_idx]
    y_train, y_test = iris_label[train_idx], iris_label[test_idx]

    #dt모델 학습하기
    kf_ml.fit(X_train, y_train)

    #예측
    kf_pred_train =kf_ml.predict(X_train)
    kf_pred_test =kf_ml.predict(X_test)

    # 정확도를 5번 측정할 것
    n_iter +=1
    acc_train = np.round(accuracy_score(y_train, kf_pred_train),4)
    acc_test = np.round(accuracy_score(y_test, kf_pred_test),4)

    #교차검증 train, test 정확도 확인
    print('\n {} 번 train 교차 검증 정확도 :{}, test의 교차검증 정확도 :{}'.format(n_iter, acc_train, acc_test))

    cv_acc_train.append(acc_train)
    cv_acc_test.append(acc_test)

print('train 평균 정확도', np.mean(cv_acc_train))
print('test 평균 정확도', np.mean(cv_acc_test))

1 번 train 교차 검증 정확도 :1.0, test의 교차검증 정확도 :1.0

2 번 train 교차 검증 정확도 :1.0, test의 교차검증 정확도 :0.9667

3 번 train 교차 검증 정확도 :1.0, test의 교차검증 정확도 :0.8667

4 번 train 교차 검증 정확도 :1.0, test의 교차검증 정확도 :0.9333

5 번 train 교차 검증 정확도 :1.0, test의 교차검증 정확도 :0.7333
train 평균 정확도 1.0
test 평균 정확도 0.9

test 교차 검증 정확도가 Fold마다 차이가 많이남

StratifiedKFold 교차검증

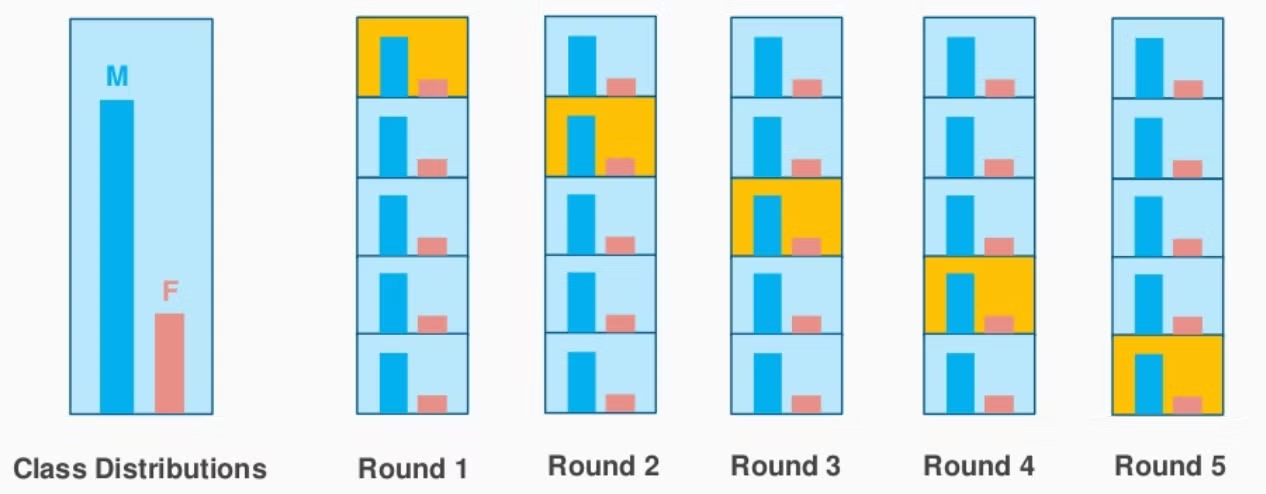
KFold 불균형 문제를 해결하기 위해서 사용

from sklearn.model_selection import StratifiedKFold
skf_iris = StratifiedKFold(n_splits=5)

n_iter = 0

skf_cv_acc_train=[]
skf_cv_acc_test=[]
skf_ml = DecisionTreeClassifier(random_state=111)

#skf 사용한 교차검증
for train_idx, test_idx in skf_iris.split(iris_data,iris_label): #skf split 안에 label
    X_train, X_test = iris_data[train_idx], iris_data[test_idx]
    y_train, y_test = iris_label[train_idx], iris_label[test_idx]

    #skf_dt모델 학습하기
    skf_ml.fit(X_train, y_train)

    #예측 (skf, split을 통해 진행)
    skf_pred_train =skf_ml.predict(X_train)
    skf_pred_test =skf_ml.predict(X_test)

    # 정확도를 5번 측정할 것

    n_iter +=1
    acc_train = np.round(accuracy_score(y_train, skf_pred_train),4)
    acc_test = np.round(accuracy_score(y_test, skf_pred_test),4)

    #교차검증 train, test 정확도 확인
    print('\n {} 번 train 교차 검증 정확도 :{}, test의 교차검증 정확도 :{}'.format(n_iter, acc_train, acc_test))

    skf_cv_acc_train.append(acc_train)
    skf_cv_acc_test.append(acc_test)

print('train 평균 정확도', np.mean(skf_cv_acc_train))
print('test 평균 정확도', np.mean(skf_cv_acc_test))

 1 번 train 교차 검증 정확도 :1.0, test의 교차검증 정확도 :0.9667

 2 번 train 교차 검증 정확도 :1.0, test의 교차검증 정확도 :0.9667

 3 번 train 교차 검증 정확도 :1.0, test의 교차검증 정확도 :0.9

 4 번 train 교차 검증 정확도 :1.0, test의 교차검증 정확도 :0.9667

 5 번 train 교차 검증 정확도 :1.0, test의 교차검증 정확도 :1.0
train 평균 정확도 1.0
test 평균 정확도 0.9600200000000001

KFold보다 Fold마다 정확도 차이가 적음

→ 데이터 불균형을 고려하여 분리하였기 때문

시계열 데이터 split

from sklearn.model_selection import TimeSeriesSplit
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# 예제 데이터셋 만들기
np.random.seed(42)
n_samples = 100

# 시계열 데이터 생성
dates = pd.date_range(start='2023-01-01', periods = n_samples)

## (추세 + 노이즈)
data = pd.DataFrame({
    'date':dates,
    'value':np.arange(n_samples) + np.random.randn(n_samples)*5
})

tscv = TimeSeriesSplit(n_splits=4)

## X, y 설정
X =  np.arange(n_samples).reshape(-1,1)
y = data['value'].values

#tscv 사용한 교차검증
mse_scores = []
fold = 1

for train_idx, test_idx in tscv.split(X): #X값으로 넣어주기
    X_train, X_test = X[train_idx], X[test_idx]
    y_train, y_test = y[train_idx], y[test_idx]

    print(len(train_idx))
    print(len(test_idx))
    #skf_dt모델 학습하기
    model = LinearRegression()
    model.fit(X_train, y_train)

    #예측
    y_pred = model.predict(X_test)
    mse = mean_squared_error(y_test, y_pred)
    mse_scores.append(mse)

    print(f'Fold {fold}:MSE = :{mse}')
    fold += 1

mean_mse = np.mean(mse_scores)
print(mean_mse)

# 실행결과
Fold 1:MSE = :106.04232691358722
Fold 2:MSE = :21.293765433933984
Fold 3:MSE = :28.73271723264395
Fold 4:MSE = :31.053362234544124
Fold 5:MSE = :10.163480004238991
39.45713036378966

import matplotlib.pyplot as plt
## 시각화
plt.figure(figsize=(10,6))
plt.plot(data['date'], y, label='True Value')
plt.plot(data['date'], model.predict(X), label='Predict VAlue', linestyle='--')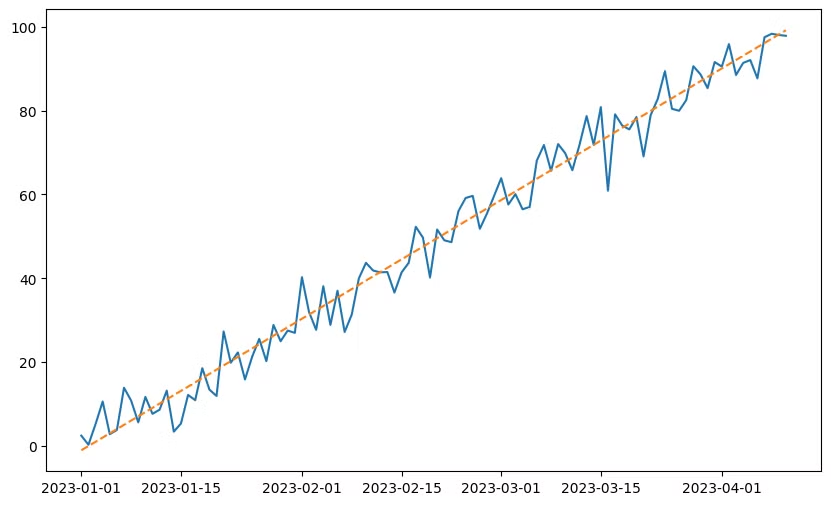

n_splits

100 개의 데이터로 시작
n_splits = 4
test_size( n_samples // (n_splits + 1))를 떼어놓고 다음과 같이 분리
첫 Fold
- trian [0~19]
- test [20~39]
두 번째 Fold
- train [0~39]
- test [40~59]
...마지막N
- train [0~79]
- test [80~99]

참고

LOOCV (Leave-One-Out Cross-Validation)

데이터셋에서 하나의 샘플만 테스트 데이터로 사용하고, 나머지 샘플을 모두 학습 데이터로 사용
- 이 과정을 모든 샘플에 대해 반복
- 즉, 데이터셋에 n개의 샘플이 있다면, n번의 학습과 평가가 이루어짐
장점 : 데이터가 적을 때 성능 평가에 유리하며, 모든 데이터를 최대한 활용
단점 : 데이터가 많아질수록 계산 비용이 크게 증가

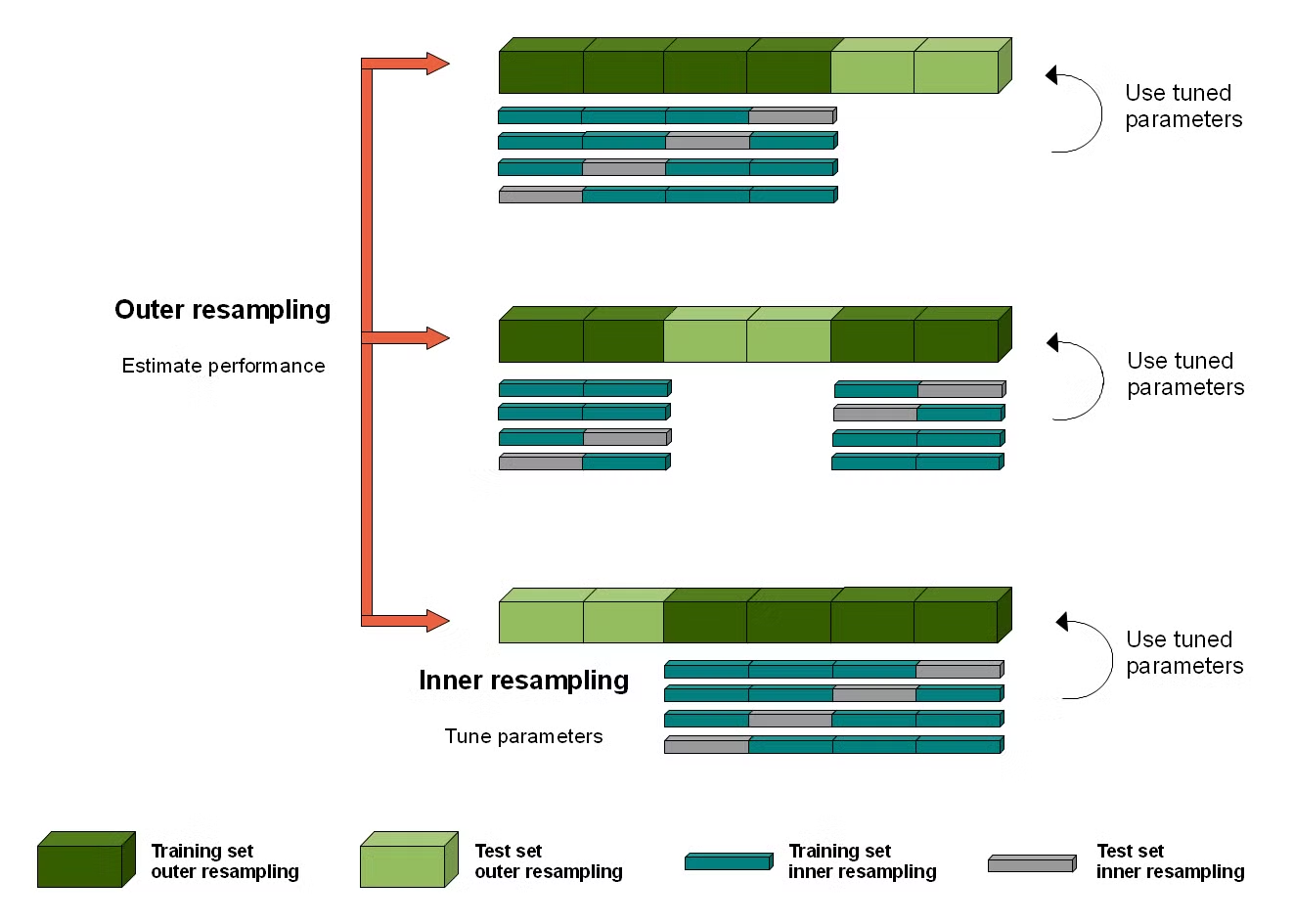
Nested Cross-Validation

Outer loop: 데이터를 K개의 폴드로 나누고, 그중 하나의 폴드를 테스트 데이터로 사용하며, 나머지 K-1개의 폴드를 학습 데이터로 사용. 이 과정을 K번 반복하여 모델 성능을 평가.
Inner loop: 각 Outer fold에서 학습 데이터를 다시 교차 검증(K-Fold)으로 나누어 하이퍼파라미터 튜닝을 진행. 즉, 학습 데이터를 K-1개로 학습하고 1개로 검증을 반복하여 최적의 하이퍼파라미터를 찾음.
- Outer loop와 Inner loop가 동시에 진행되며, 하이퍼파라미터 튜닝과 성능 평가를 분리해서 수행.
하이퍼파라미터 최적화 시 모델 성능을 과대평가하는 문제를 방지할 수 있음.
데이터가 크거나 하이퍼파라미터 튜닝이 복잡할 경우 계산 비용이 크게 증가.