
임계값 조정
재현율과 정밀도
재현율(Recall)
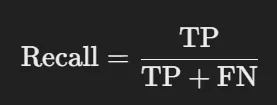
- 실제로 '양성'(TP + FN)인 것들 중에서 내가 맞게 찾아낸(TP) 비율
- 예를 들어, 병을 앓고 있는 사람을 모두 찾는 게 목표라면, 재현율은 아픈 사람을 얼마나 잘 찾아냈는지 보여주는 지표이다
- 재현율이 높을수록 실제 양성(아픈 사람)을 더 잘 찾아낸 것
정밀도(Precision)

- '양성'이라고 예측한 것들(TP +FN) 중에서 실제로 '양성'(TP)인 비율
- 예를 들어, 병에 걸렸다고 예측한 사람들이 실제로도 병에 걸렸는지 보여주는 지표이다.
- 정밀도가 높을수록 양성이라고 예측한 사람 중 실제 양성인 사람이 많아, 예측이 더 정확한 것
Trade off
- 정밀도와 재현율은 서로 Trade off 관계이다.
- 임계값(Threshold) : 양성과 음성을 구분하는 기준값입니다.
- 예를 들어, 확률 예측에서 0.5를 임계값으로 설정
- 예측 확률 ≥ 0.5 → 양성
- 예측 확률 < 0.5 → 음성
- 임계값에 따른 변화
- 임계값이 작아질 때
- 양성으로 예측하는 비율을 높여 재현율을 높인다.
- 잘못된 양성 예측이 많아져 정밀도가 낮아진다.
- 임계값이 높아질 때
- 판별의 기준 값이 올라가 확신하는 경우에만 양성으로 예측하여 정밀도는 높아진다.
- 양성으로 예측하는 비율이 줄어들어 재현율이 낮아진다.
- 임계값이 작아질 때
임계값 조정
Binarizer
- 주어진 데이터를 특정 임계값(threshold)을 기준으로 0과 1로 변환하는 함수이다.
예시
from sklearn.preprocessing import Binarizer
X = [[1,0,-1],
[3,0,2],
[0,1.3,1.5]]
# 임계값 1을 기준으로 이진 변환
binarizer = Binarizer(threshold=1)
print(binarizer.fit_transform(X))[[0. 0. 0.]
[1. 0. 1.]
[0. 1. 1.]]응용
라이브러리 및 데이터 불러오기
import pandas as pd
import seaborn as sns
import numpy as np
df = sns.load_dataset('diamonds')
df.head()이진 분류 문제로 변환
df['cut_binary'] = df['cut'].apply(lambda x: 1 if x in ['Premium', 'Ideal'] else 0)- Premium 이상인 경우 1, 그렇지 안으면 0으로 바꿈
수치형 변수만 사용 (문제를 단순화하기 위함)
df_sp = df[['depth', 'table', 'price', 'x', 'y', 'z', 'cut_binary']]train/test 분리
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(df_sp.drop('cut_binary',axis=1), df_sp['cut_binary'], test_size=0.3, random_state=111)평가 지표 함수 생성
from sklearn.metrics import accuracy_score, confusion_matrix, precision_score, recall_score
def get_clf_eval(y_test, pred):
confusion = confusion_matrix(y_test, pred)
accuracy = accuracy_score(y_test, pred)
precision = precision_score(y_test, pred, average='micro')
recall = recall_score(y_test, pred, average='micro')
print('오차 행렬')
print(confusion)
print(f'정확도: {accuracy:.4f}, 정밀도: {precision:.4f}, 재현율: {recall:.4f}')모델 학습 (LogisticRegression)
from sklearn.linear_model import LogisticRegression
lr_clf = LogisticRegression(max_iter = 500)
lr_clf.fit(X_train, y_train)
pred = lr_clf.predict(X_test)
get_clf_eval(y_test, pred)오차 행렬
[[2861 2719]
[1012 9590]]
정확도: 0.7694, 정밀도: 0.7694, 재현율: 0.7694pred_proba 확인
pred_proba = lr_clf.predict_proba(X_test)pred_proba(): 머신러닝 모델, 특히 분류 모델에서 각 클래스에 속할 확률을 예측하는 함수
(핵심) 임계값 조정을 위해 Binarizer 선언 및 조정에 따른 결과
from sklearn.preprocessing import Binarizer
binarizer = Binarizer(threshold=0.3)
tt_pred = binarizer.fit_transform(pred_proba)[:,1].reshape(-1, 1)
get_clf_eval(y_test, tt_pred)오차 행렬
[[ 1311 4269]
[ 128 10474]]
정확도: 0.7283, 정밀도: 0.7283, 재현율: 0.7283- 임계값이 0.3일때 결과 확인
임계값 조정에 따른 metric값 그래프 변화 출력
from sklearn.metrics import f1_score
import matplotlib.pyplot as plt
thresholds= [0.3,0.4,0.5,0.6,0.7,0.8]
def get_eval_list(y_test, pred_proba, thresholds):
accuracy_tt_list = []
precision_tt_list = []
recall_tt_list = []
f1_tt_list = []
for threshold in thresholds:
binarizer = Binarizer(threshold=threshold)
tt_pred = binarizer.fit_transform(pred_proba)[:,1].reshape(-1, 1)
accuracy_tt = accuracy_score(y_test, tt_pred)
precision_tt = precision_score(y_test, tt_pred)
recall_tt = recall_score(y_test, tt_pred)
f1_tt = f1_score(y_test, tt_pred)
accuracy_tt_list.append(accuracy_tt)
precision_tt_list.append(precision_tt)
recall_tt_list.append(recall_tt)
f1_tt_list.append(f1_tt)
return accuracy_tt_list, precision_tt_list, recall_tt_list, f1_tt_list
def figure_eval(accuracy_tt_list, precision_tt_list, recall_tt_list, f1_tt_list, thresholds):
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
metrics = [accuracy_tt_list, precision_tt_list, recall_tt_list, f1_tt_list]
titles = ['Accuracy', 'Precision', 'Recall', 'F1 Score']
for i, ax in enumerate(axes.flat):
ax.plot(thresholds, metrics[i], marker='o')
ax.set_title(titles[i])
ax.set_xlabel('Threshold')
ax.set_ylabel('Score')
plt.show()
accuracy_list, precision_list, recall_list, f1_list = get_eval_list(y_test, pred_proba, thresholds)
figure_eval(accuracy_list, precision_list, recall_list, f1_list, thresholds)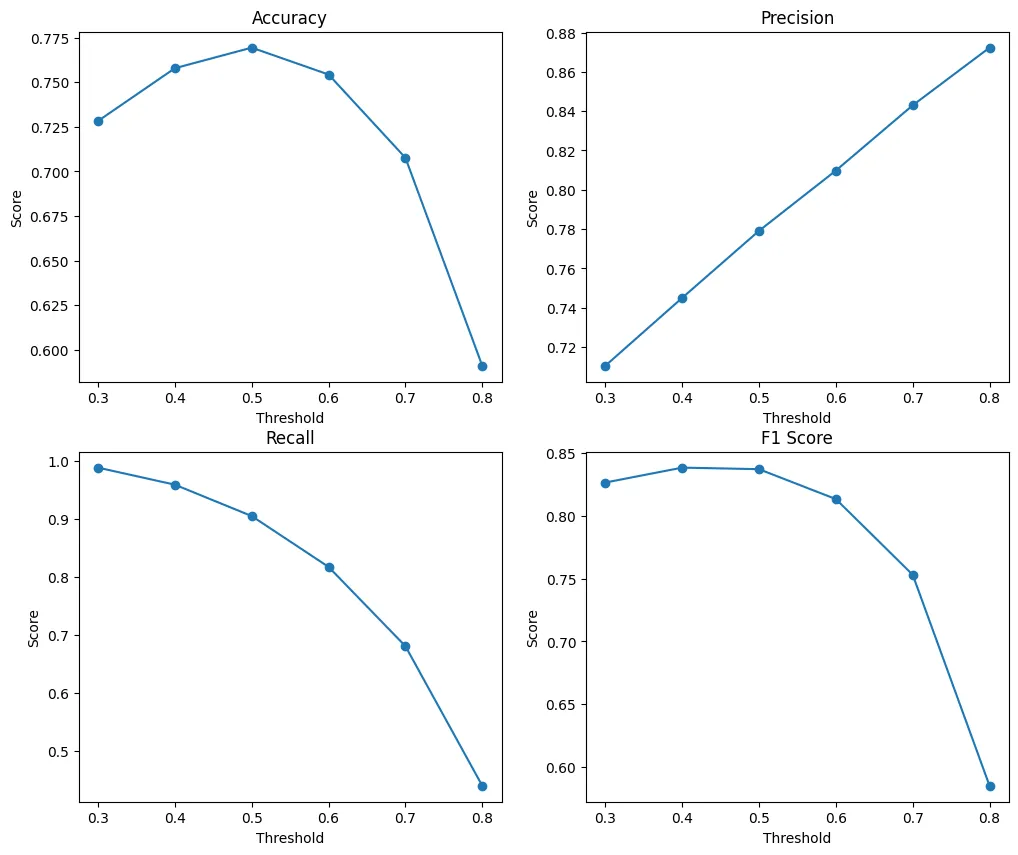
- Threshold에 따라 평가지표들이 변함
- F1 score를 기준으로 0.4 ~ 0.5 사이의 값을 선택하는 것이 좋아보인다.
K-Nearest Neigborhood (KNN)
- 회귀, 분류 모두 가능한 Memory-based learning이다.
- 학습 과정에서 데이터를 일반화하거나 모델 파라미터를 학습하지 않고, 예측 시점에서 데이터 간의 거리 계산을 통해 즉시 예측하는 방식
- 알고리즘 순서
- 거리 계산: 새로운 데이터 포인트와 모든 훈련 데이터 간의 거리를 계산한다. (주로 유클리드 거리 사용)
- 가장 가까운 K개 이웃 선택: 거리값을 기준으로 가장 가까운 K개의 이웃을 선택한다.
- 예측 수행:
- 분류: 선택한 K개의 이웃 중 다수결로 클래스를 예측한다.
- 회귀: K개의 이웃의 평균 또는 가중 평균으로 값을 예측한다.
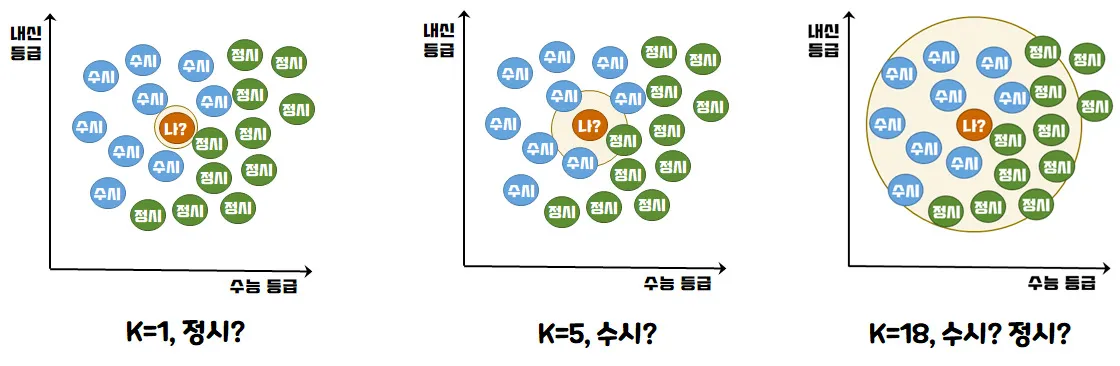
K 값의 영향
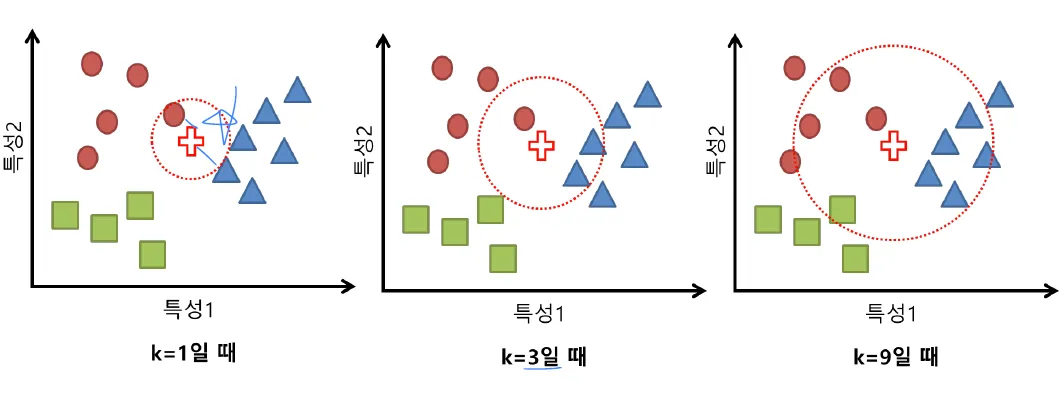
- K의 크기에 따라 KNN의 성능이 크게 달라집니다.
- 작은 K 값: 모델이 훈련 데이터에 민감해져 과적합(overfitting)될 가능성이 있다.
- 큰 K 값: 모델이 훈련 데이터의 세부 정보를 잃고, 오히려 과소적합(underfitting)될 수 있다.
Majority Voting (다수결 방식)
- 클래스 불균형이 있는 경우, 단순 다수결로는 적은 수의 클래스를 제대로 반영하지 못할 수 있다.
- 가까운 이웃일수록 더 큰 영향력을 갖도록 거리 가중치를 부여해 성능을 개선
중요한 변수와 불필요한 변수 구분 필요성
- KNN은 모든 변수에 동일한 비중(거리로 계산하므로)을 두므로 중요하지 않은 변수가 있으면 성능이 저하될 수 있다.
- 중요한 변수만 선택(feature selection)하거나 특성 스케일링(feature scaling)을 통해 성능을 높이는 것이 좋습니다.
변수 유형
종속변수
- 범주형 변수
- 가장 많이 나타나는 범주를 선택하여 예측
- 동률 발생(Tie)을 막기 위해 k를 홀수로 설정하는 것이 좋음
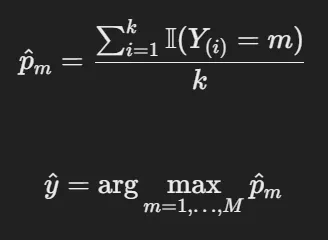
- 수치형 변수
- 이웃 값의 평균으로 예측
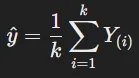
- 거리에 반비례하는 가중평균(Weighted Average) 방식도 고려 가능.
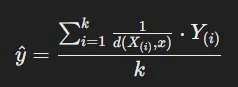
- 이웃 값의 평균으로 예측
독립 변수 (거리 선택 방식)
- 범주형 변수
- Hamming distnace : 다른 위치의 개수를 계산
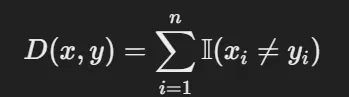
- Hamming distnace : 다른 위치의 개수를 계산
- 수치형 변수
- Euclidean Distance : 두 점 사이의 직선 거리 계산
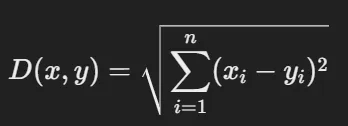
- Manhattan Distance : 두 점 사이의 직교 경로를 따라 이동한 거리를 계
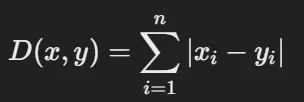
- Euclidean Distance : 두 점 사이의 직선 거리 계산
