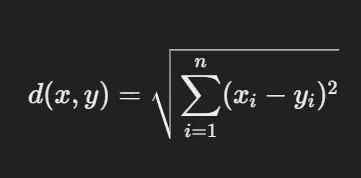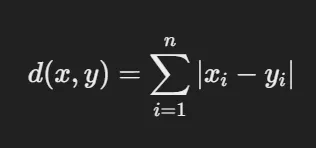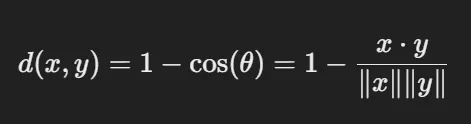[BDA 데이터분석모델링반(ML1)] 5주차 KNN 알고리즘2

YJ·2024년 11월 18일

BDA python sklearn 데이터 분석 머신러닝 전처리

BDA 데이터분석모델링반(ML1)

목록 보기

5/7

K-Nearest Neigborhood (KNN)

이전 글의 후반부에서 다루었던 내용이다.
- 참고 링크 : [BDA 데이터분석모델링반(ML1)] 4주차 임계값 조정 및 KNN 알고리즘
예측 시점에서 데이터 간의 거리 계산을 통해 즉시 예측하는 방식

💡 목표
KNN을 라이브러리 없이 밑바닥부터 구현해보고 Sklearn 라이브러리를 사용하여 구현하기

구현

밑바닥부터 구현하기

거리 계산: 새로운 데이터 포인트와 모든 훈련 데이터 간의 거리를 계산한다. (주로 유클리드 거리 사용)
가장 가까운 K개 이웃 선택: 거리값을 기준으로 가장 가까운 K개의 이웃을 선택한다.
예측 수행:
- 분류: 선택한 K개의 이웃 중 다수결로 클래스를 예측한다.
- 회귀: K개의 이웃의 평균 또는 가중 평균으로 값을 예측한다.

라이브러리 불러오기

import numpy as np
from collections import Counter
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

💡 KNN 분류

임의의 분류 데이터 생성하기

np.random.seed(42)

n_samples = 100
X = np.random.uniform(low=0, high=10, size=(n_samples, 2))
X_train, X_test = train_test_split(X, test_size=0.1, random_state=42)
y_train = np.random.choice([0, 1], size=X_train.shape[0])

100개의 샘플 데이터 생성
Train data 90개 / test 데이터 10개 분류

거리 선언하기

# 맨해튼 거리
def manhattan_distance(x1, x2):
	return np.abs(x1 - x2).sum()
	
# 유클리디안 거리
def euclidean_distance(x1, x2):
    return np.sqrt(np.sum((x1-x2)**2))

KNN Classifier 선언

def knn_classifier(X_train, y_train, X_test, distance, k):
    y_pred = []
    for x_test in X_test:
        distances = [distance(x_test, x_train) for x_train in X_train]
        k_indices = np.argsort(distances)[:k]
        k_nearest_labels = [y_train[i] for i in k_indices]
        most_common = Counter(k_nearest_labels).most_common(1)
        y_pred.append(most_common[0][0])

        # 시각화
        plt.figure(figsize=(8, 6))
        plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap='bwr', marker='o', label='Training Dataset')
        plt.scatter(x_test[0], x_test[1], s=150, label='Test Data', marker='*')

        # 거리 방식에 따라 시각화 변경
        if distance.__name__ == 'manhattan_distance':
            for idx in k_indices:
                x1, y1 = X_train[idx]
                x2, y2 = x_test
                plt.plot([x1, x1], [y1, y2], 'k--', alpha=0.5)  # 세로 이동
                plt.plot([x1, x2], [y2, y2], 'k--', alpha=0.5)  # 가로 이동
        elif distance.__name__ == 'euclidean_distance':
            for idx in k_indices:
                x1, y1 = X_train[idx]
                x2, y2 = x_test
                plt.plot([x1, x2], [y1, y2], 'k--', alpha=0.5)  # 직선 연결

        plt.title(f"KNN Classifier (k={k}) - Predicted Label: {most_common[0][0]}")
        plt.legend()
        plt.show()

    return np.array(y_pred)

KNN 분류 (k = 5, 맨해튼 거리)

k = 5
y_pred = knn_classifier(X_train, y_train, X_test, manhattan_distance, k)
print('KNN 예측 값', y_pred)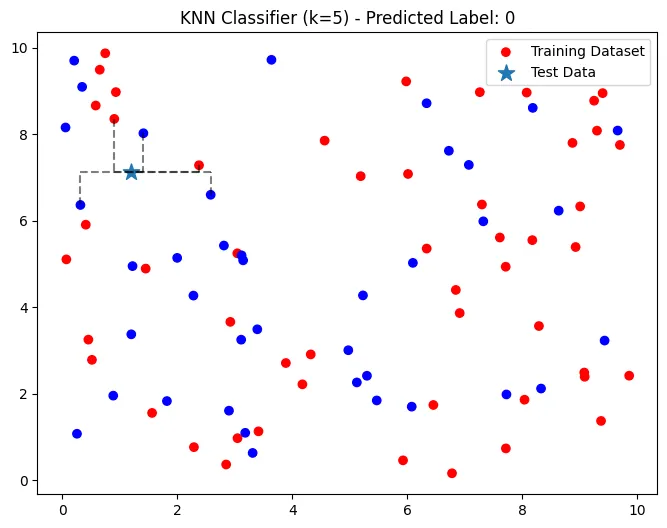

다수결에 의해 0으로 분류
- 빨간색 - label → 1
- 파란색 - label → 0

KNN 분류 (k = 5, 유클리디안 거리)

k = 3
y_pred = knn_classifier(X_train, y_train, X_test, euclidean_distance, k)
print('KNN 예측 값', y_pred)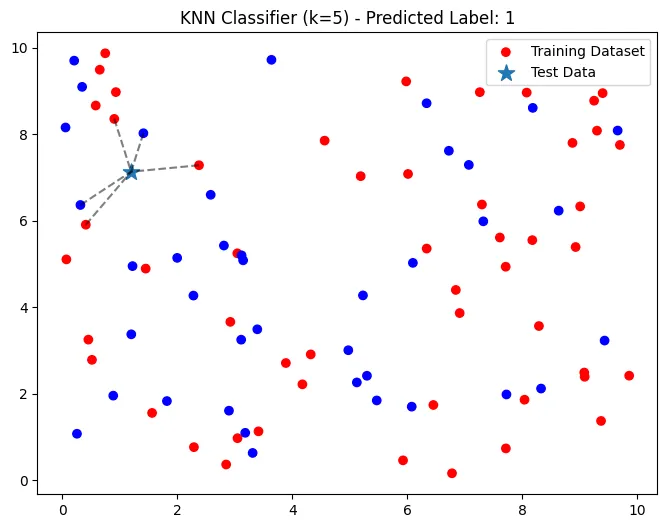

다수결에 의해 1로 분류
- 빨간색 - label → 1
- 파란색 - label → 0

💡 KNN 회귀

임의의 회귀 데이터 생성하기

np.random.seed(42)

n_samples = 100
X = np.random.uniform(low=0, high=10, size=(n_samples, 2))
X_train, X_test = train_test_split(X, test_size=0.1, random_state=42)

noise = np.random.normal(loc=0, scale=1, size=X_train.shape[0])  # 랜덤 노이즈
y_train = 2 * X_train[:, 0] + 3 * X_train[:, 1] + noise

KNN Regressor 선언

def knn_regressor(X_train, y_train, X_test, distance, k):
    y_pred = []
    for x_test in X_test:
        distances = [distance(x_test, x_train) for x_train in X_train]
        k_indices = np.argsort(distances)[:k]
        k_nearest_labels = [y_train[i] for i in k_indices]
        mean_value=np.mean(k_nearest_labels)
        y_pred.append(mean_value)

        ## 시각화 추가
        plt.figure(figsize=(8,6))
        plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap='bwr',marker='o',label='Traning Data')
        plt.scatter(x_test[0], x_test[1], s=150,label='Test Data',marker='*')

        # 거리 방식에 따라 시각화 변경
        if distance.__name__ == 'manhattan_distance':
            for idx in k_indices:
                x1, y1 = X_train[idx]
                x2, y2 = x_test
                plt.plot([x1, x1], [y1, y2], 'k--', alpha=0.5)  # 세로 이동
                plt.plot([x1, x2], [y2, y2], 'k--', alpha=0.5)  # 가로 이동
        elif distance.__name__ == 'euclidean_distance':
            for idx in k_indices:
                x1, y1 = X_train[idx]
                x2, y2 = x_test
                plt.plot([x1, x2], [y1, y2], 'k--', alpha=0.5)  # 직선 연결

        plt.title(f"KNN regressor (k={k}) - Predicted Label :{mean_value:.2f}")
        plt.legend()
        plt.show()

    return np.array(y_pred)

KNN 회귀 (k = 5, 맨해튼 거리)

k = 3
y_pred =knn_regressor(X_train, y_train, X_test, manhattan_distance, k)
print('KNN 예측 값',y_pred)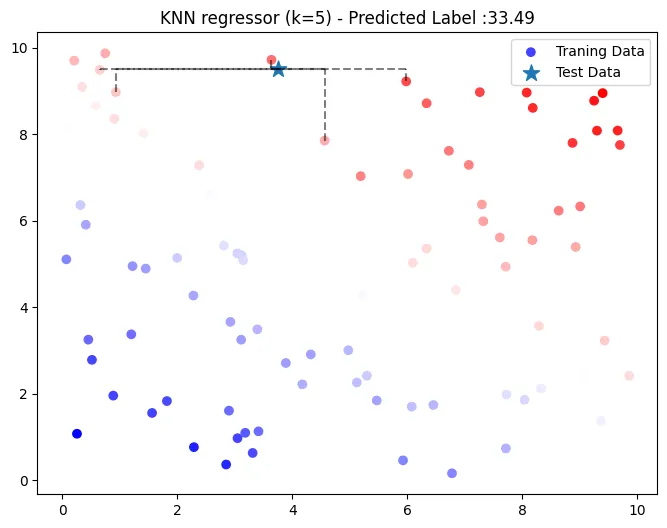

가중평균에 의해 33.49로 예측
- [37.25 31.70, 40.09, 28.91, 29.49] 의 가중평균

KNN 회귀 (k = 5, 유클리디안 거리)

k = 5
y_pred =knn_regressor(X_train, y_train, X_test, euclidean_distance, k)
print('KNN 예측 값',y_pred)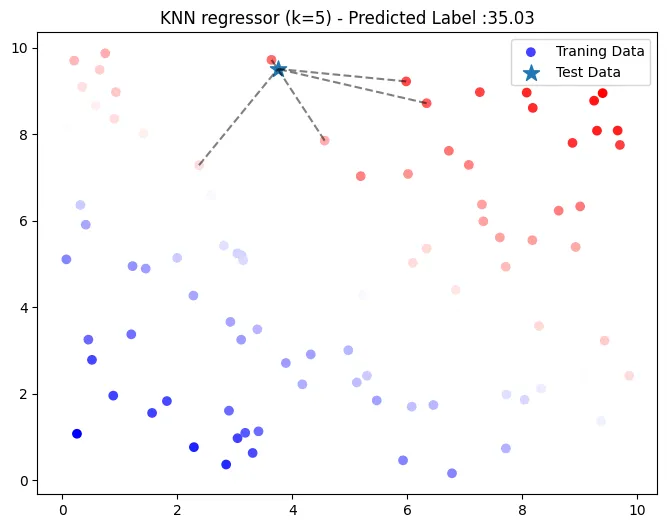

가중평균에 의해 35.03로 예측 (test 데이터 [7.31993942, 5.98658484])
- [37.25, 31.70, 40.087 27.55, 38.58] 의 가중평균

→ 데이터의 양과 차원이 변화함에 따라 선택한 거리 측정(metric) 방식이 KNN 알고리즘의 성능에 중요한 영향을 미칠 수 있다.

💡 거리 측정(metric) 방식 종류

유클리디드 거리 (Euclidean Distance)

정의: 두 점 사이의 직선 거리(유클리드 거리)로, 가장 일반적으로 사용되는 거리 계산 방식

활용: 저차원 연속형 데이터.

수식:

맨해튼 거리 (Manhattan Distance)

정의: 각 축의 거리 합으로 계산. 택시가 격자형 도로망을 따라 이동하는 방식과 비슷

활용: 격자형/이산형 데이터.

수식:

코사인 거리 (Cosine Similarity)

특징: 정의: 벡터 간의 각도를 기반으로 거리를 측정. 두 벡터가 얼마나 유사한 방향을 가지는지 평가

활용: 고차원 데이터

수식:

민코프스키 거리 (Minkowski Distance)

정의: 유클리드 거리와 맨해튼 거리의 일반화된 형태로, p 값을 조정하여 다양한 거리 계산 방식을 제공

활용: 데이터 특성에 맞춘 거리 계산.

수식 !

💡 (중요) 데이터 스케일링

축 간의 스케일이 다를 경우, 스케일링(정규화)을 반드시 수행한 후 적합한 거리 측정 방식을 선택

💡 Weighted KNN

가중치를 거리의 역수로 설정하여 가까운 이웃이 더 큰 영향을 미치도록 설계
수식 :
즉, 가까운 이웃 (dᵢ가 작을수록) 중요도가 더 높아진다.

가중치 추가 비교 (KNN 회귀)

def knn_regressor(X_train, y_train, X_test, distance, k):
    y_pred = []
    for x_test in X_test:
        distances = [distance(x_test, x_train) for x_train in X_train]
        k_indices = np.argsort(distances)[:k]
        k_nearest_labels = [y_train[i] for i in k_indices]
        mean_value=np.mean(k_nearest_labels)
        y_pred.append(mean_value)
    return np.array(y_pred)

def knn_weighted_regressor(X_train, y_train, X_test, distance, k, beta = 1):
    y_pred = []
    for x_test in X_test:
        distances = np.array([distance(x_test, x_train) for x_train in X_train])
        k_indices = distances.argsort()[:k]
        k_nearest_labels = [y_train[i] for i in k_indices]
        k_distances = distances[k_indices]

        #거리 가중치 계산 추가
        weights = 1/(k_distances ** beta + 1e-8)
        weighted_mean = np.sum(weights * k_nearest_labels) / np.sum(weights)

        y_pred.append(weighted_mean)
    return np.array(y_pred)

새로운 데이터 정의

np.random.seed(0)

n_samples = 50
X_train = np.random.uniform(low=0, high=10, size=(n_samples, 1))
y_train = np.sin(X_train).ravel() + np.random.normal(0,0.5,n_samples)
X_test = np.linspace(0,10,100).reshape(-1,1)

sin 함수에 noise(정규분포에서 임의로 뽑음)가 섞인 형태로 정의된 데이터이다.

k=5
#knn 회귀
y_pred_knn=knn_regressor(X_train,y_train, X_test, euclidean_distance,k)

#가중치 회귀
y_pred_weighted_knn=knn_weighted_regressor(X_train, y_train, X_test, euclidean_distance, k)

#실제값과 비교
y_true = np.sin(X_test).ravel()

# 시각화
plt.figure(figsize=(12,6))
plt.scatter(X_train, y_train, color='black', label='Training Data')
plt.plot(X_test, y_true, color='green', label = 'True')
plt.plot(X_test, y_pred_knn, color='blue',linestyle='--', label = 'knn')
plt.plot(X_test, y_pred_weighted_knn, color='red',linestyle='--', label = 'knn_weighted')
plt.title('KNN 비교')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()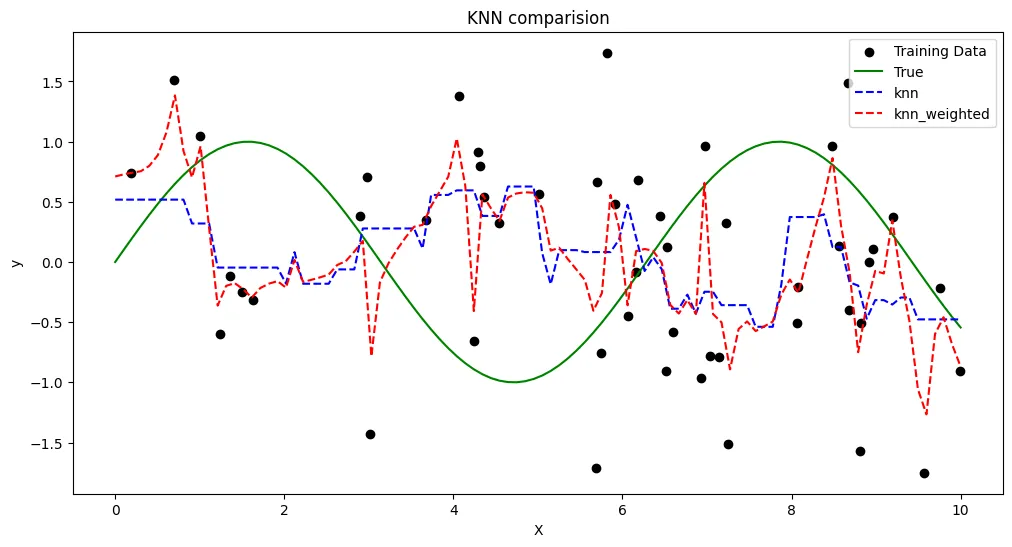

검은 점: 노이즈가 포함된 훈련 데이터
녹색 선: 이상적인 sin 함수 (노이즈 없음)
파란 점선 (KNN): 모든 이웃에 동일한 가중치, 예측이 부드럽지만 세부 패턴을 놓칠 수 있음
빨간 점선 (가중 KNN): 가까운 이웃에 더 높은 가중치, 국소적 패턴을 더 잘 반영하지만 노이즈에 민감

→ Weighted KNN은 훈련 데이터의 세밀한 패턴을 더 잘 반영한다.

Sklearn 라이브러리를 활용한 구현

분류의 예제만 다룸

라이브러리 불러오기

from sklearn.neighbors import KNeighborsClassifier

분류 예제 데이터 생성

X_train = np.array([[1, 2], [2, 3], [3, 3], [6, 5], [7, 8], [8, 8]])
y_train = np.array([0, 0, 0, 1, 1, 1])  # 클래스 라벨
X_test = np.array([[3, 4], [5, 5]])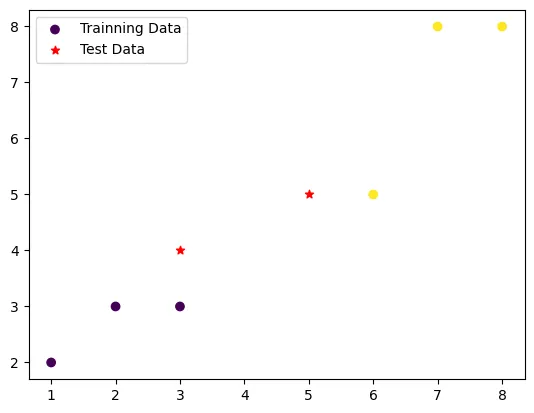

KNN classifier 생성 및 학습 (k = 3)

knn_cl=KNeighborsClassifier(n_neighbors=3).fit(X_train,y_train)

fit은 훈련 데이터에 맞게 학습시키는 과정이지만, KNN은 거리 기반 알고리즘이므로 훈련 데이터를 단순히 저장하는 것이다.

예측

y_pred = knn_cl.predict(X_test)
print("Predicted Class:", y_pred)

[0, 0] 으로 분류

선택된 이웃 정보 확인

distances, indices = knn_cl.kneighbors(X_test)
print("Distances to Neighbors:", distances)
print("Indices of Neighbors:", indices)

선택된 이웃과 해당 이웃의 라벨 출력

# 선택된 이웃
neighbors = X_train[indices]
print("Neighbors:\n", neighbors)

# 선택된 이웃의 라벨
neighbor_labels = y_train[indices]
print("Labels of Neighbors:", neighbor_labels)

Sklearn KNN 하이퍼파리미터 정리

하이퍼파라미터	설명	가능한 값	default
`n_neighbors`	이웃의 수 kkk: 예측에 사용할 가장 가까운 데이터 포인트의 수	정수	`5`
`weights`	가중치 결정 방법: 이웃의 기여도를 결정	`'uniform'`, `'distance'`	`'uniform'`
`metric`	거리 측정 방식	`'euclidean'`, `'manhattan'`, 기타 사용자 정의 거리 함수	`'minkowski'` (p=2: 유클리드)
`algorithm`	거리 기반 탐색 방식: 이웃 탐색에 사용되는 알고리즘 선택	`'auto'`, `'ball_tree'`, `'kd_tree'`, `'brute'`	`'auto'`

auto : 데이터 특성에 따라 적합한 알고리즘을 자동 선택.
ball_tree : Ball Tree로 공간 분할, 효율적 탐색. 고차원 데이터에 적합.
kd_tree : KD Tree로 차원 축소 및 효율적 탐색. 중간 차원 데이터에 적합.
brute : 완전 탐색 방식, 작은 데이터나 정확도가 중요한 경우 사용.

제 글이 유익하셨다면 ♡와 팔로우로 응원 부탁드립니다.

이전 포스트

[BDA 데이터분석모델링반(ML1)] 4주차 임계값 조정 및 KNN 알고리즘

다음 포스트

[BDA 데이터분석모델링반(ML1)] 5주차 KNN 알고리즘2