이 블로그글은 2019년 조재영(Kevin Jo), 김승수(SeungSu Kim)님의 딥러닝 홀로서기 세미나를 수강하고 작성한 글임을 밝힙니다.

History of DL / MLP Basic

History of DL

Structure of Neuron

• 머신러닝 기법으로는 모델을 미리 정해줘야하고 특정한 문제에만 사용할 수 밖에 없다는 한계가 존재했음

→ 사람처럼 생각하는 모델을 만들자

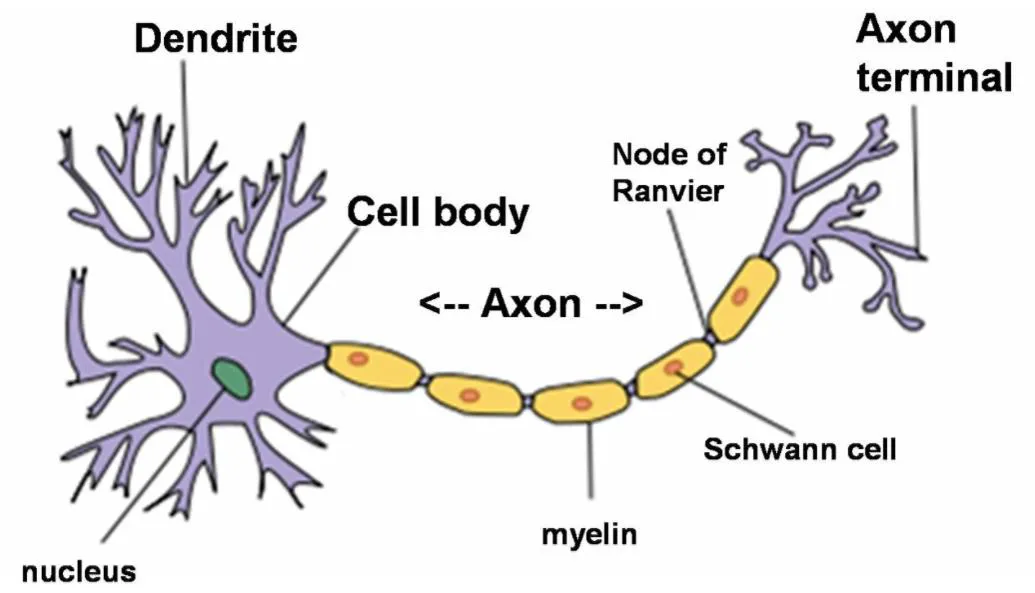
• 신호를 조합해서 다른 뉴런으로 전달하는 구조

Modeling Neuron (1957)

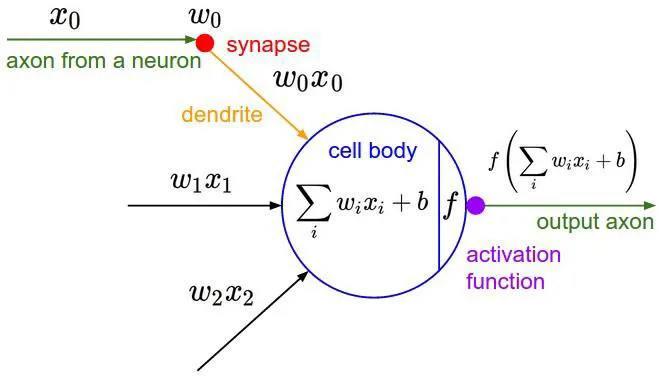
• 아래의 것들로 계산 한 값이 특정 역치 값을 넘으면 신호 전달
  • x0, x1, x2 : 이전 뉴런으로부터 들어온 신호
  • w0, w1, w2 : 가중치
  • b : 바이어스
• activation function을 가지고 구현해 놓음
  • 대부분의 activation function은 non-linear 함

→ 인공신경망이라고 부름

💡Activation function
신경망에서 입력 신호를 비선형으로 변환해, 모델이 복잡한 패턴을 학습할 수 있도록 하는 함수

• Sigmoid: 출력 값을 0과 1 사이로 압축해주는 함수.
• ReLU (Rectified Linear Unit): 음수는 0으로, 양수는 그대로 반환하는 함수.
• Tanh: 출력 값을 -1과 1 사이로 압축하는 함수.
• Leaky ReLU: 음수도 작은 기울기로 유지해주는 ReLU의 변형.
• Softmax: 다중 클래스 확률 분포를 계산하는 함수.

And/Or Problem

• 인공 신경망을 이용해서 And/Or 문제를 해결하려고 했음

→ XOR 문제는 해결하지 못함

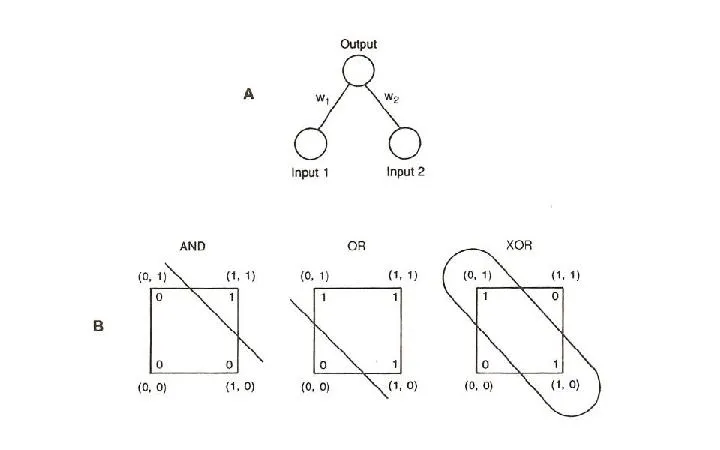
💡 And/Or/Xor

• AND: 두 입력이 모두 1일 때만 1을 출력.
• OR: 두 입력 중 하나라도 1이면 1을 출력.
• XOR: 두 입력이 다를 때만 1을 출력.

진리표

A	B	AND (A ∧ B)	OR (A ∨ B)	XOR (A ⊕ B)
0	0	0	0	0
0	1	0	1	1
1	0	0	1	1
1	1	1	1	0

Multilayer Perceptron (1969)

• XOR 문제를 해결함
• input layer와 output layer를 제외하고 hiden layer가 하나 이상 있는 신경망

→ 당시, 수학적으로는 증명했으나 학습을 할 수는 없다는 결론을 내림

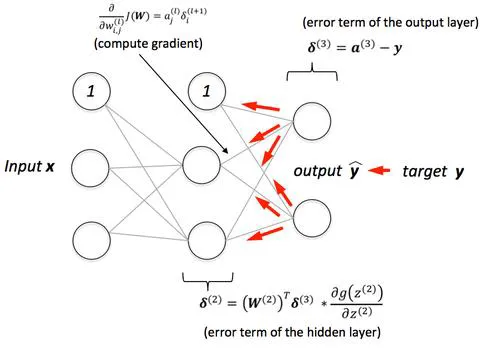
Backpropagation (1986)

• Multilayer Perceptron을 훈련시킬 수 있는 알고리즘이 등장함
• output과 target과의 loss를 계산하고 이러한 loss를 줄이기 위해 네트워크를 거꾸로 따라가면서 그래디언트를 계산하고 가중치를 조정해나감

→ 여전히 Training 과정이 복잡하다는 문제점이 있었음

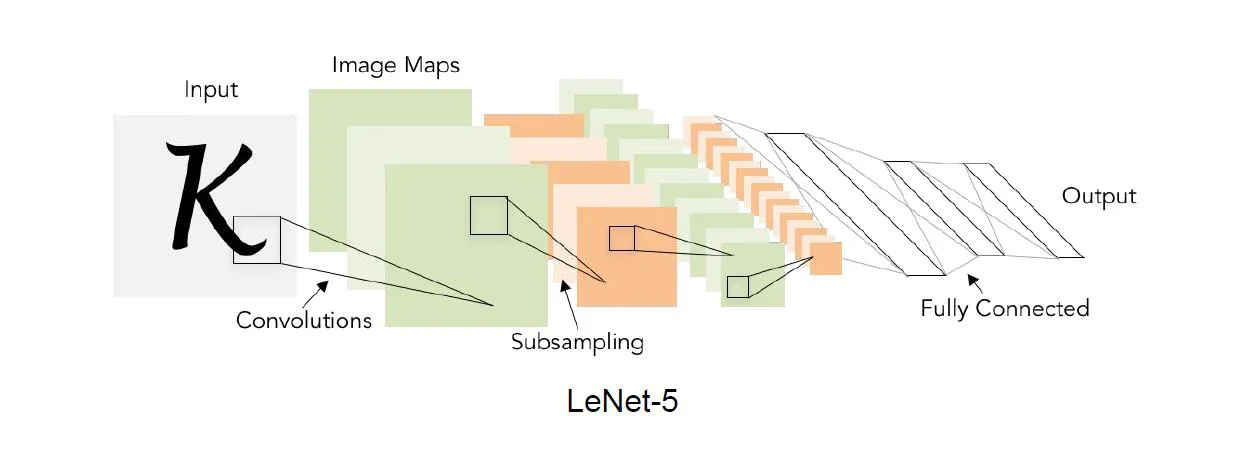
Convolutional Neural Networks (2012)

• 사람들이 이미지를 볼 때 이미지 전체를 다 보는것이 아니라 조각조각 나눠서 보고 합치는 것이 아닐까?
• 처음에는 이미지의 작은 조각(예: 모서리나 간단한 패턴)들을 인식하고, 뒤로 갈수록 점점 더 큰 조각(예: 얼굴, 자동차 등)을 인식하고 이렇게 작은 부분에서 큰 부분으로 점점 확장하며 이미지를 이해한다.

→ ImageNet Classification 문제에 큰 기여, 현재는 사람보다 더 분류를 잘하는 모델을 개발됨

MLP Basic

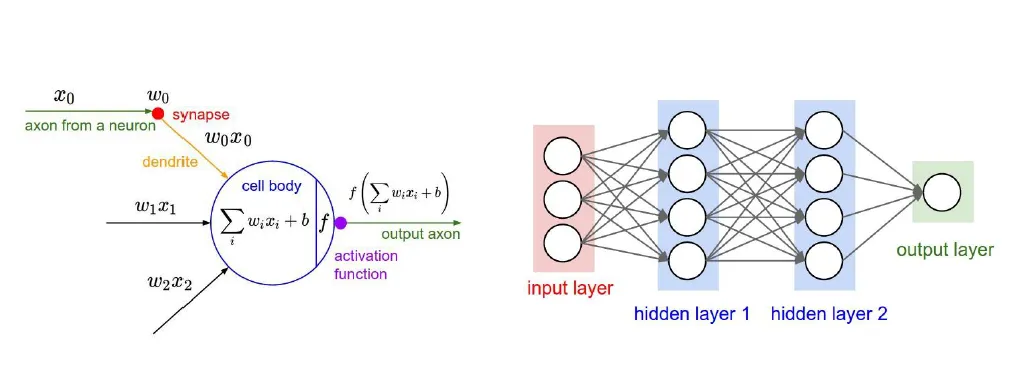
MLP

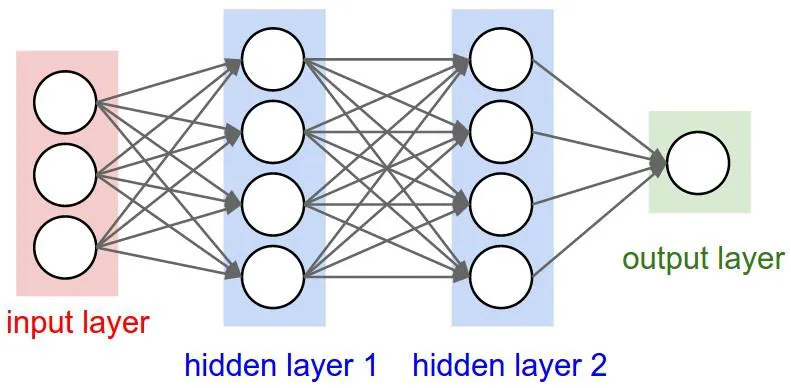
• 여러 층의 노드로 구성된 신경망으로, 입력 데이터를 처리해 결과를 출력하는 모델
  • Input Layer: 데이터를 입력하는 층.
  • Hidden Layer: 특징을 학습하는 중간층.
  • Output Layer: 최종 결과를 출력하는 층.
  • Hidden Unit: 각 층의 노드(뉴런).
  • 화살표: 가중치를 곱하고 활성화 함수를 적용한 값을 전달함.

→ 가중치 W와 편향 b만을 가지고 XOR 문제를 해결했다.

→ 하지만 어떻게 훈련을 시킬 수 있을까?

Universal Approximation Theorem

• 단일 은닉층을 가진 신경망(단층 네트워크)이 이론적으로는 어떤 연속적인 함수라도 근사할 수 있음
  • 하지만, 이를 위해 필요한 은닉층의 노드 수가 매우 많아질 수 있고, 실제로 학습이 어렵거나 비효율적일 수 있음
• 깊은 신경망(즉, 여러 개의 은닉층을 가진 네트워크)을 사용하면 더 적은 노드 수로도 효율적으로 원하는 함수를 표현하고 학습할 수 있게 됨

→ 단층 네트워크도 이론적으로는 모든 함수를 표현할 수 있지만, 현실적으로는 깊은 신경망을 사용하는 것이 더 효율적이다.

Backpropagation

• 연쇄 법칙을 통해 손실을 줄이는 방향으로 가중치를 조정하는 과정
• 머신러닝 알고리즘들과 Optimizer도 모두 같은 원리로 작동함
  • 다만, Chain rule을 이용해 각 층의 가중치에 대해 손실의 미분을 계산하여 가중치를 업데이트함

💡 뉴런 학습의 과정

• Feed Forward: 입력 데이터를 통해 예측 값을 계산함.
• Backpropagation: 손실을 계산하고, 가중치를 조정하여 모델을 학습함