구분구적법

• 곡선 f(x)의 [a, b] 구간에서의 정적분 값을 근사적으로 계산하기 위한 수치적분 중 하나로, 곡선 f(x)와 x축사이의 면적을 도형들의 합으로 근사하여 구한다.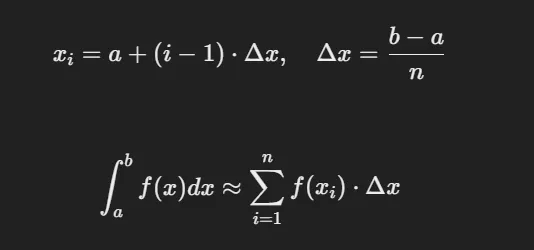
  

MATLAB 예시

주어진 그래프

fun = @(x) exp(-x).*sin(x);
x = 0:0.01:10;
plot(x, fun(x))

• 구간 0 ~ 10까지 구분구적법을 통한 계산

구분구적법을 통한 계산

fun = @(x) exp(-x).*sin(x);

a = 0; b=10;
n=100000;
isum=0;
for i = 1:n
    isum = isum + fun(a+((b-a)/n)*(i-1))*((b-a)/n);
end
isum

isum =

    0.5000

integral()을 통한 계산

integral()

• 주어진 함수에 대해 수치적으로 적분을 계산하는 함수
  • 형식 : Q = integral(fun, a, b)
    • 입력값
      • fun : 적분할 함수
      • a, b : 적분 구간의 시작점과 끝점
    • 출력값
      • Q: 적분값(스칼라 값).

fun = @(x) exp(-x).*sin(x);

q = integral(fun, a, b)

q =

    0.5000

이 경우 구분구적법을 이용한 계산과 integral() 함수로 계산한 값이 동일하다.

정적분의 수치적 근사: 직사각형 법칙과 사다리꼴 법칙 비교

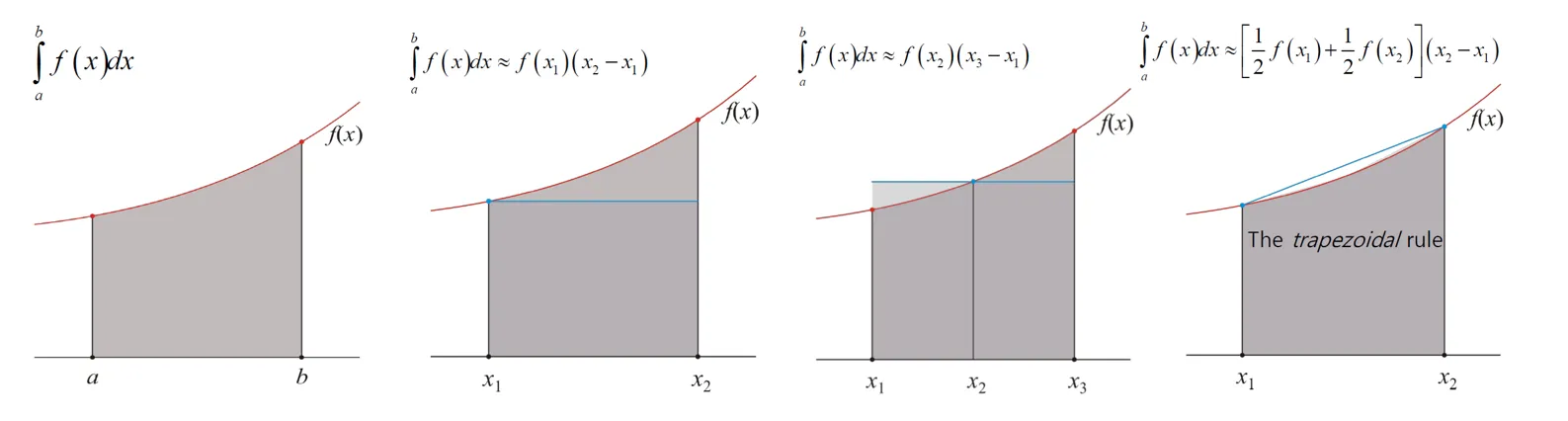
• 수학에서 적분값을 정확히 계산하기 어려울 때, 곡선 아래의 면적을 수치적으로 근사하는 다양한 방법이 사용된다.
• 1번 이미지 : 정적분
  • 함수 f(x)를 [a,b]구간에서 구한 정확한 적분값
• 2번 이미지: 직사각형 법칙 (왼쪽 끝점 기준)
  • 함수 f(x)를 [a,b]구간에서 왼쪽 끝점 x1에서의 함수값을 직사각형의 높이로 사용
  • 곡선의 형태를 제대로 반영하지 못할 수 있어 부정확한 근사값일 수 있다.
• 3번 이미지: 직사각형 법칙 (중간값을 이용)
  • 함수 f(x)를 [a,b]구간에서 x1 ,x2의 중점에서의 함수값을 직사각형의 높이로 사용
  • 조금 더 정확한 근사값을 나타낼 수 있다.
• 4번 이미지 : 사다리꼴 법칙 (The Trapzoidal rule)
  • 곡선을 사다리꼴로 근사하여 면적을 계산
  • 직사각형 법칙보다 더 높은 정확도를 제공한다.

적분에 대한 수치적 근사를 할 때 어떤 방식을 적용하냐에 따라 정확도가 달라진다.