로지스틱 맵 (Logistic map)

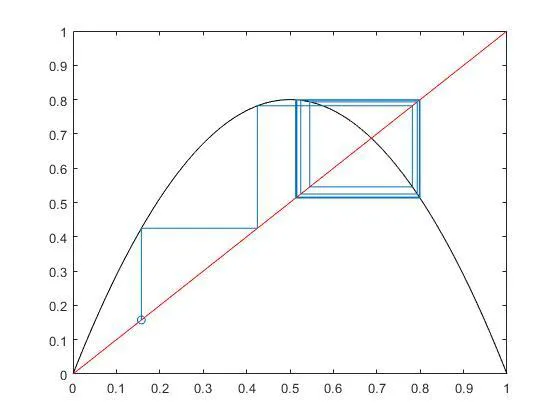
• 비선형 동역학 시스템의 모델로, 주로 혼돈 이론과 주기적 행동을 연구하는 데 사용된다.
  
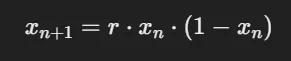
  • 참고 링크 : 위키피디아 Logistic map
  • 비선형 동역학 : 시스템의 상태가 시간에 따라 변화하는 방식을 연구하는 분야
• 이 맵은 특정 매개변수에 따라 수렴이나 주기적 반복, 혼돈 상태로의 전환을 보이는 특성을 가진다.
• 이 시스템은 인구 성장, 생태학적 모델링, 경제 모델, 사회적 현상 등 여러 분야에서 적용될 수 있다.
• r값에 따른 변화
  • 0 < r ≤ 1 : 모든 값이 0으로 수렴 (멸종)
  • 1 < r ≤ 3 :값이 특정 고정점으로 수렴
  • 3 < r ≤ 3.57 :값이 주기적 궤도(2주기, 4주기 등)로 변함
  • 3.57 <r ≤4
    • 혼돈 상태(Chaos)로 진입
      • 혼동 상태 : 복잡하고 예측불가능한 운동
    • 값이 무작위처럼 보이며, 초기 조건(x₀)에 극도로 민감하다. (나비 효과)
      • 나비 효과 : 작은 변화가 시간이 지남에 따라 큰 결과를 초래할 수 있는 현상
  • r > 4
    • 값이 발산하여 시스템이 정의된 범위 (0≤x≤1)를 벗어남
    • Logistic Map이 더 이상 물리적으로 의미를 가지지 않음

예시

MATLAB 코드

Logistic Map에서 특정 값 r에 따른 궤적을 시각화

clear all;
clf
r = 3.2; 
map = @(r, x) r * x .* (1-x);
x = 0:0.01:1; plot(x, map(r, x), 'k');
hold on; plot(x, x, 'r')

x0 = rand;
x1 = map(r, x0); plot(x0, x0, 'o');
n = 30;
for i = 1:n
    line([x0 x0], [x0 x1]);
    line([x0 x1], [x1 x1]);
    x0 = x1; x1 = map(r, x0);
end

• 그래프에서 나타나는 궤적은 초기 값 x0와 r에 따른 Logistic Map 방정식의 반복 과정을 Cobweb Plot으로 시각화한 것이다.
  • Cobweb Plot : 이산적 비선형 시스템에서 반복 과정을 시각화한 그래프로, 함수f(x)와 대각선 y=x를 이용해 궤적을 표현한다. 이를 통해 고정점, 주기 궤도, 혼돈 상태 등 시스템의 동적 거동을 직관적으로 이해할 수 있다.
• r = 3.2 : 결국엔 특정값에 수렴하는 것을 보여줌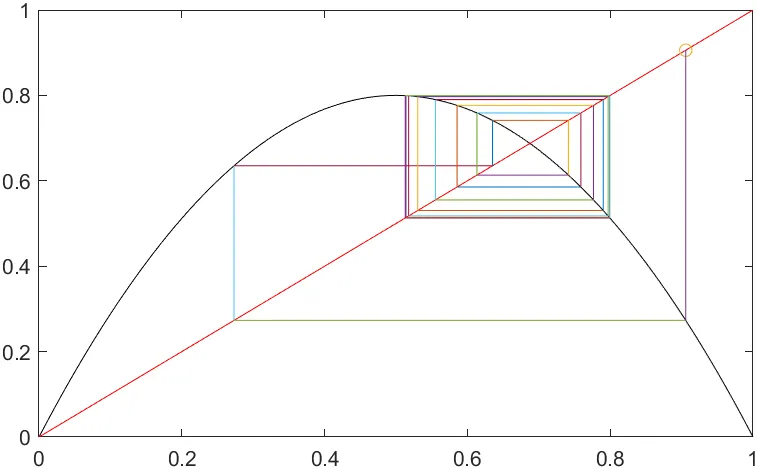

-r > 3.57 : 값이 특정값에 수렴하지 못하고 혼동 상태

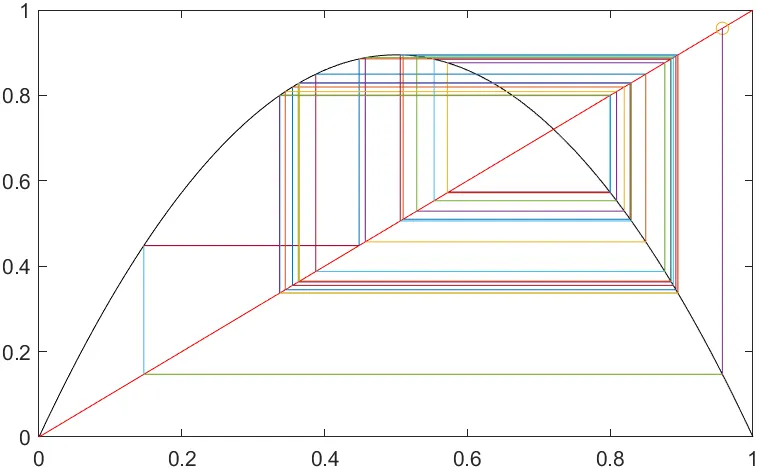
• r > 4 : 값이 발산하여 정의된 범위를 벗어나 비정상적인 상태를 나타냄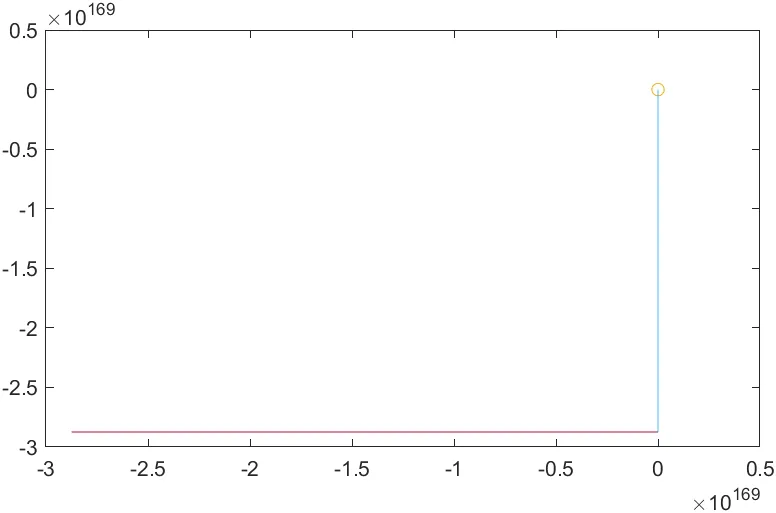
  

Logistic Map의 r에 따른 주기 배가 범위 시각화

clear all; clf
r = 3.2;
map = @(r,x) r * x.*(1-x);
xx = []; 

x0 = rand;
xx = [1 x0; xx];
n = 100;
for i = 2:n
	x1 = map(r, x0);
	xx = [i x1; xx]; x0 = x1;
end
plot(xx(:, 1), xx(:,2), 'o')

Logistic Map의 주기 배가 범위

• 주기 배가 현상 : r이 증가하면 주기가 다음과 같은 순서로 두 배로 증가, 혼동 현상까지 지속

  • 1→2→4→8→16→32→…

• 1 < r ≤ 3 : 값이 특정 고정값으로 수렴합니다.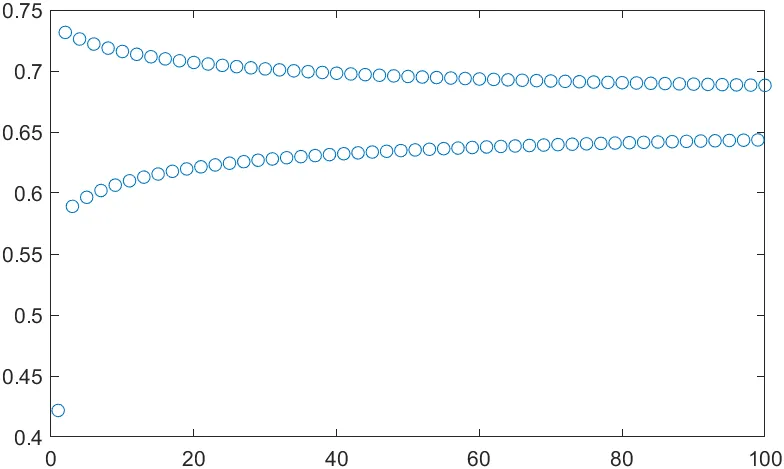

  
  

• 3 < r ≤ 3.449 : 2주기 발생, 고정점 대신 두 개의 값 사이에서 반복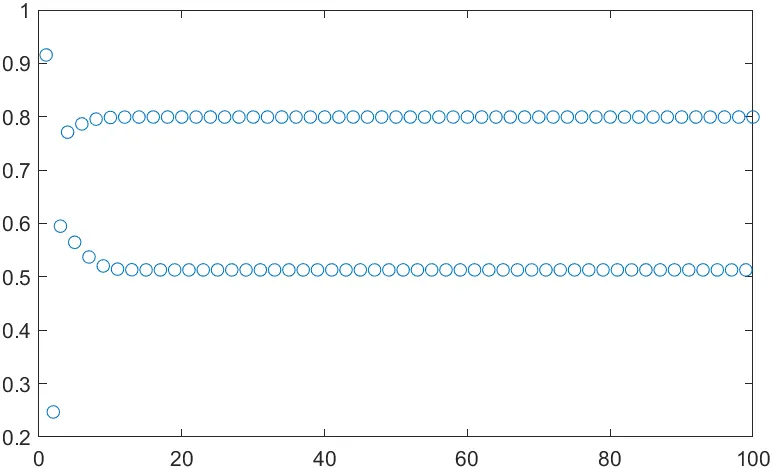

  
  

• 3.449 < r ≤ 3.544 : 4주기 발생, 네 개의 값 사이에서 반복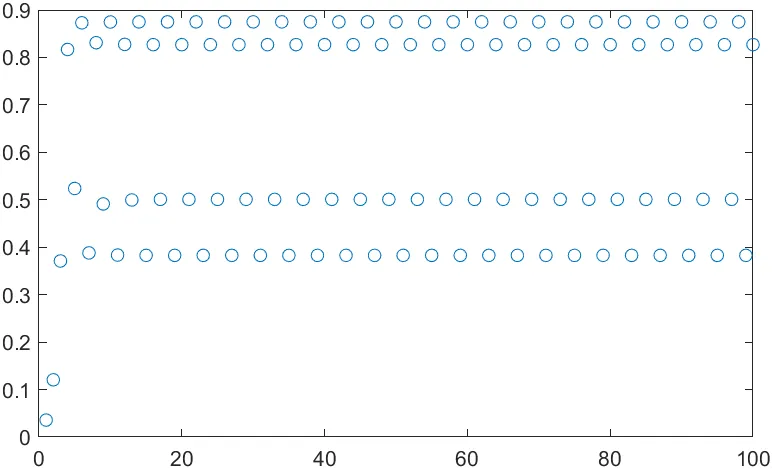

  
  

• 3.544 < r ≤ 3.564 : 8주기 발생, 여덟 개의 값 사이에서 반복

  

• r ≥ 3.57 : 주기가 무한히 복잡해지며 혼돈이 발생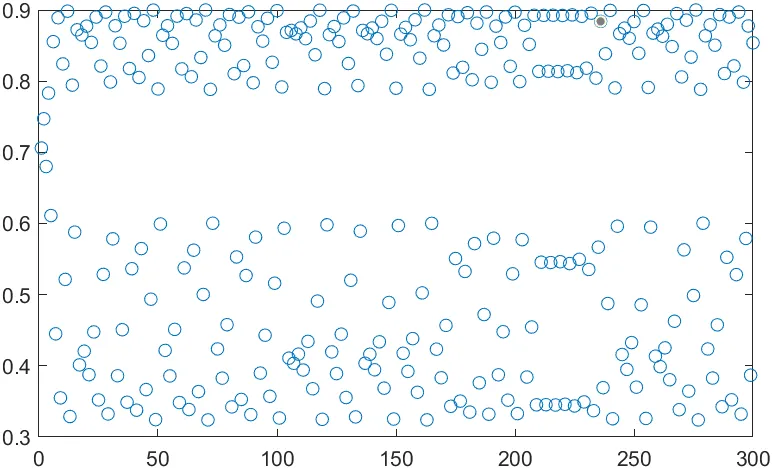

  

반복 이후에 r 값에 따른 logistic map 값 시각화

clear all; clf
map = @(r,x) r*x.*(1-x);
for r = 2:0.001:4
	x0 = rand;
	for j = 1:10000
		x1 = map(r, x0); x0 = x1;
	end
	pp = [];
	for j = 1:100
		x1 = map(r, x0); pp = [r x1;pp];
		x0 = x1;
	end
	plot(pp(:,1), pp(:,2), '.', 'markersize', 2);
hold on
end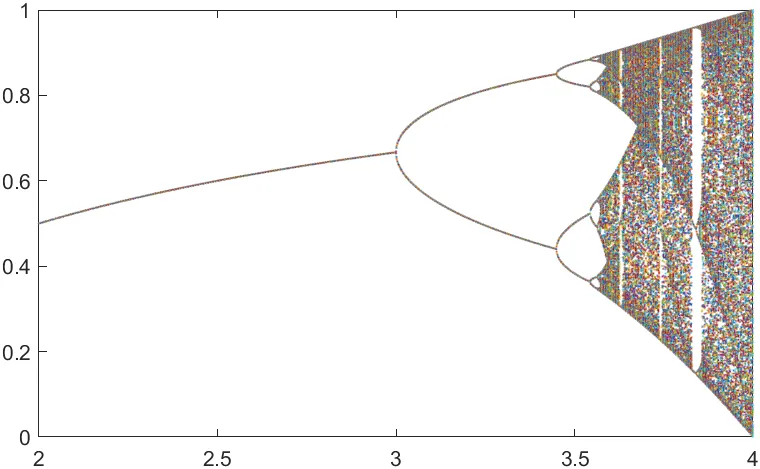 

• Logistic map의 수렴 값이 주기 배가 현상에 의해 점차적으로 증가하는 모습을 보여준다.
• 특히, r ~= 3.58 부근에서 혼동상태에 돌입함을 나타낸다.