[MATLAB] 행렬과 배열 2/2

산술연산자와 관계 연산자

산술연산자

• 우선순위 : 수학 연산의 우선순위와 동일
• 점 연산자(.*, ./, .\, .^) : 배열에서 원소 끼리 연산 수행

기호	역할
+	덧셈
-	뺼셈
*	곱셈
.*	요소별 곱셈
/	오른쪽나눗셈
./	요소별 오른쪽 나눗셈
\	왼쪽나눗셈
.\	요소별 왼쪽나눗셈
^	거듭제곱
.^	요소별 거듭제곱
‘	켤레복소수전치
.’	전치

>> a = [1 2 3;4 5 6;7 8 9];
>> a+a(1)

ans =

     2     3     4
     5     6     7
     8     9    10

>> a+a % 행렬 덧셈

ans =

     2     4     6
     8    10    12
    14    16    18

>> a*a % 행렬 곱셈

ans =

    30    36    42
    66    81    96
   102   126   150

>> a.*a % 행렬 요소별 곱셈

ans =

     1     4     9
    16    25    36
    49    64    81

>> a' % 행렬 전치

ans =

     1     4     7
     2     5     8
     3     6     9

>> a.^a % 행렬 요소별 제곱

ans =

           1           4          27
         256        3125       46656
      823543    16777216   387420489

>> a./a % 행렬 요소별 오른쪽나눗셈

ans =

     1     1     1
     1     1     1
     1     1     1

>> a/a % 행렬 오른쪽나눗셈
 

ans =

     1     0     0
     0     1     0
     0     0     1

>> a.\a % 행렬 요소별 왼쪽나눗셈

ans =

     1     1     1
     1     1     1
     1     1     1

>> a\a % 행렬 왼쪽 나눗셈

ans =

    1.0000    0.5000         0
         0         0         0
         0    0.5000    1.0000

• a / b, a * inv(b) 둘은 같은 표현
• a\b, inv(a) * b 둘은 같은 표현

Nonconjugated Transpose, Conjugated Transpose

• Nonconjugated Transpose (전치 행렬) : 단순히 행렬의 행과 열을 바꾸는 것
• Conjugated Transpose (켤레 전치 행렬) : 전치 행렬을 구한 후 복소수 부분의 부호를 반전시킨 것

>> a = [1 2-i;3+i 4]

a =

   1.0000 + 0.0000i   2.0000 - 1.0000i
   3.0000 + 1.0000i   4.0000 + 0.0000i

>> a.'

ans =

   1.0000 + 0.0000i   3.0000 + 1.0000i
   2.0000 - 1.0000i   4.0000 + 0.0000i

>> transpose(a)

ans =

   1.0000 + 0.0000i   3.0000 + 1.0000i
   2.0000 - 1.0000i   4.0000 + 0.0000i

>> a'

ans =

   1.0000 + 0.0000i   3.0000 - 1.0000i
   2.0000 + 1.0000i   4.0000 + 0.0000i

출력형식

• 기본 출력 형식은 format 명령어로 바꿀 수 있다.
• format 명령어가 실행된 이후의 모드 출력은 규정된 형식으로 표시된다.

명령어	설명	예: 100/3
format short	0.01<수≤1000인 수를 소수점 이하 네 자리 수의 고정소수점으로 표시함. 그 외의 범위의 수는 short e 형식으로 표시함	ans = 33.3333
format long	0.01<수≤1000인 수를 소수점 이하 15자리의 고정소수점으로 표시함. 그 외의 범위의 수는 long e 형식으로 표시함	ans = 33.333333333333336
format short e	소수점 이하 네 자리수의 과학적 표기법으로 표시함	ans = 3.3333e+0.1
format long e	소수점 이하 15 자리수의 과학적 표기법으로 표시함	ans = 3.333333333333334e+01
format short g	고정소수점 표시와 부동소수점 표시 중에서 더 편한 방법으로 표시. 유효숫자는 5개	ans = 33.333
format long g	고정소수점 표시와 부동소수점 표시 중에서 더 편한 방법으로 표시. 유효숫자는 15개	ans = 33.3333333333333

내장함수

• 수학 내장 함수

함수	설명	예
sqrt(x)	제곱근	sqrt(81) = 9
nthroot(x, n)	실수 x의 실수 n 제곱근 (x 가 음수이면, n은 홀수 정수이어야 함)	nthroot(80, 5) = 2.4022
exp(x)	지수함수	exp(5) = 148.4132
abs(x)	절대값	abs(-24) = 24
log(x)	자연로그, 밑이 e인 로그(ln)	log(1000) = 6.9078
log10(x)	밑이 10인 로그	log10(1000) = 3
factorial(x)	계승함수 x!
(x는 양의 정수이어야 함)	factorial(5) =120
sin(x). sind(x)	각도 x의 사인(x는 라디안), 각도 x의 사인(x는 도)	sin(pi/6) = 0.5000
cos(x), cosd(x)	각도 x의 코사인(x는 라디안), 각도 x의 코사인(x는 도)	cosd(30) = 0.8660
tan(x), tand(x)	각도 x의 탄젠트(x는 라디안), 각도 x의 탄젠트(x는 도)	tan(pi/6) = 0.5774
cot(x), cotd(x)	각도 x의 코탄젠트(x는 라디안), 각도 x의 코탄젠트(x는 도)	cotd(30) = 1.7321

• 쌍곡삼각함수 : sinh, cosh, tanh, coth

• 통계 관련 함수 : rand, randn, mean, std, var, max, min, hist, abs, median

• 배열을 다룰 때 편리한 함수 : size, length, find, short, reshape

• hist : 히스토그램을 그림

  • hist(x, bins)의 경우 bins는 간격의 개수

>> x = randn(1, 500000); % 정규분포에서 500000개의 수를 뽑음
>> hist(x) % 간격 설정 안함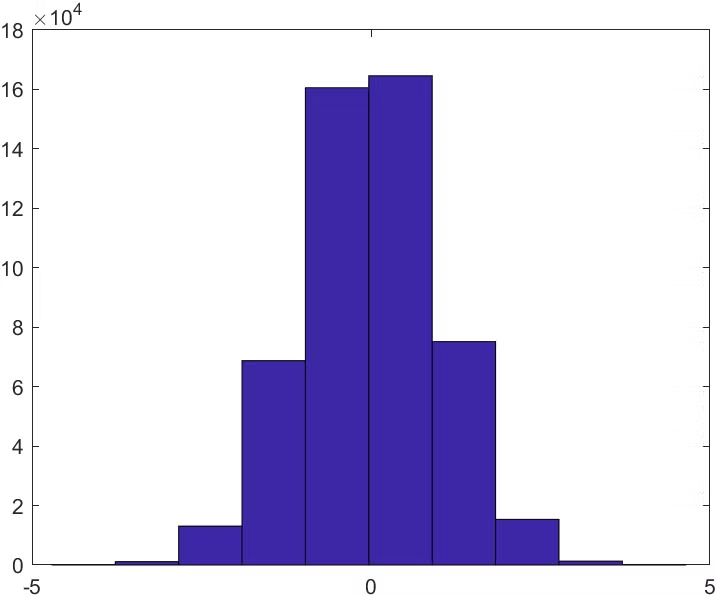

>> hist(x, 1000) % 간격 설정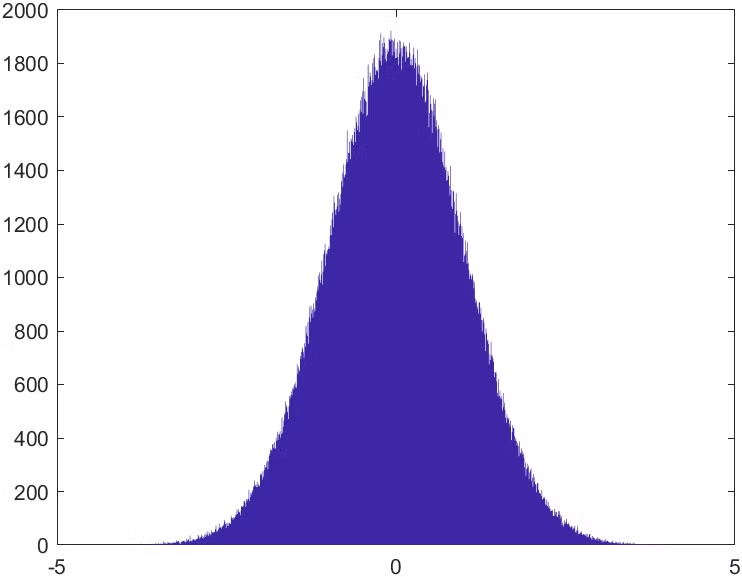

내장 변수(미리 정의된 변수)

• MATLAB에서 자주 사용하는 미리 정의된 변수
• i나 j같은 변수는 복소수가 포함되지 않으면 반복문과 관련하여 다른 변수로 정의하기도 함

변수	설명
ans	가장 최근의 계산값을 저장하고 있는 임시변수
eps	두 수 사이의 최소 차이로 2^-52 (matlab에서 표시할 수 있는 0에 가장 가까운 수)
i, j	허수
Inf	무한히 큰 수
NaN	Not-a-Number. e.g 0/0
pi	π

Round-off functions

함수	설명	예
fix	0을 기준으로 반올림	fix([-2.33 2.66]) = -2 2
floor	-∞를 기준으로 반올림	floor([-2.33 2.66]) = -3 2
ceil	+∞를 기준으로 반올림	ceil([-2.33 2.66]) = -2 3
mod	나머지 연산 (항상 양수 나머지를 반환). mod(a,b) == a -floor(a./b) * b	mod(26, 5) = 1, mod(-26, 5) = 4
round	가장 가까운 정수 기준으로 반올림	round([-2.33 2.66]) = -2 3
rem	나머지 연산 (나머지의 부호는 나누어지는 수의 부호를 따름). rem(a,b) == a-fix(a./b)*b	rem(26, 5) = 1, rem(-26, 5) = -1
sign	부호 반환	sign([-2.33 2.66]) = -1 1

Scalar 연산과 Vector 연산 차이

연산	Scalar	Vector
x + 10	x + 10	x + 10
x/5	x/5	x/5
sinx	sin(x)	sin(x)
√x	sqrt(x)	sqrt(x)
1/x	1/x	1./x
xy	x*y	x.*y
x^y	x^y	x.^y
sinxcosx	sin(x)*cos(x)	sin(x).*cos(x)
sin(x)^2	sin(x)^2	sin(x).^2
exp(x) /sqrt(x)	exp(x) /sqrt(x)	exp(x) /sqrt(x)
e^(x^2)	exp(x^2)	exp(x.^2)
1 / (x^2 + y^2)	1 / (x^2 + y^2)	1 ./ (x.^2 + y.^2)

sum(A)

• A가 벡터이면, 각 요소의 합을 반환
• A가 행렬면, 각 행끼리 합한 열벡터 반환
  • sum(A’)’ or sum(A, 2) : 각 열끼리 합한 행벡터 반환

>> a = [1 2 3 4 7]

a =

     1     2     3     4     7

>> sum(a)

ans =

    17

>> a = [1 2 3 4 7; 1 6 3 -6 -3]

a =

     1     2     3     4     7
     1     6     3    -6    -3

>> sum(a)

ans =

     2     8     6    -2     4