이 블로그글은 2017년 스탠포드 대학교 강의인 CS231n 을 시청하고 정리한 글임을 밝힙니다.

Image Classifcation Pipeline

Image Classification

• 미리 정해진 카테고리 레이블이 존재함
• 이미지를 보고 어떤 카테고리에 속할지 고르는 것

→ 기계에게는 어려운 문제일 수 있음

문제점

Semantic Gap

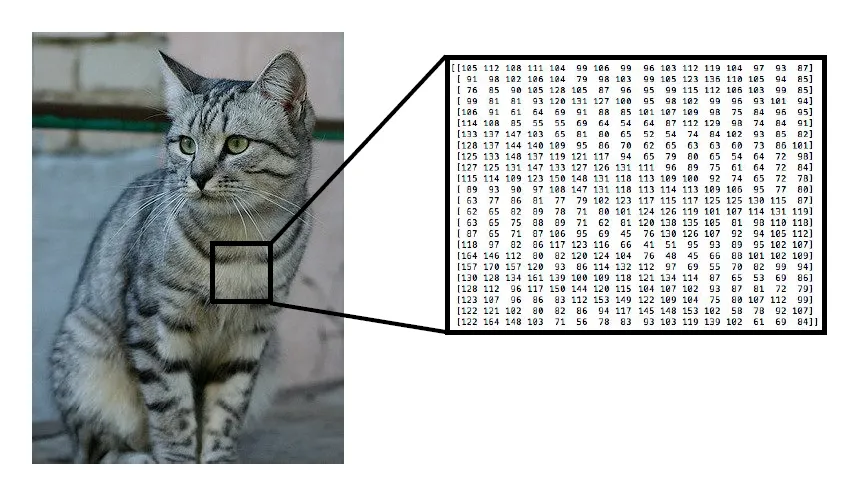
• 컴퓨터에게는 단지 숫자 집합(픽셀)로 밖에 보이지 않는다.
• “고양이”라는 레이블은 인간이 이미지에 붙인 의미상의 레이블이다.

→ 이러한 차이를 Semantic gap이라고 한다.

Viewpoint variation

• 이미지는 미묘한 변화에도 모든 픽셀 값이 모조리 달라진다.

→ 이러한 것에 알고리즘은 robust 해야한다.

💡 robust

• 알고리즘이 다양한 조건, 오류, 또는 예상치 못한 입력 상황에서도 효과적이고 신뢰성 있게 작동하는 것을 의미한다.

Illumination

• 어떤 장면이냐에 따라 조명은 각양각생일 것이다,.

→ 어두운 곳에 있던 밝은 곳에 있던 같은 레이블로 분류해야할 것이다. (robust 해야한다.)

Deformation

• 객체 자체의 변형이 있을 수 있다.

→ 다양한 변형에도 robust 해야한다.

Occulusion

• 객체가 가려질 수 있다.

→ 이러한 것에도 robust 해야한다. (아주 어려운 문제)

Background clustter

• 객체가 배경과 비슷한 경우

Intraclss variation

• 하나의 클래스 내에도 다양성이 존재한다.

우리가 어떤 객체라도 잘 다룰 수 있는 프로그램을 원한다면 더 어려운 문제이다.
→ 일부 제한된 상황을 가정한다면, 잘 작동하고 인간의 정확도와 맞먹으면 서 수행속도가 짧은 프로그램을 만들 수 있다.

Image classifier

• Soriting하는 것과 같은 hard-code로 해결되는 명시적인 알고리즘과는 달리 객체를 인식하는 명시적인 알고리즘을 구현하기 위한 적절한 묘안이 존재하지 않는다.

→ 명시적으로 해결하는 code rule을 만들려는 시도가 있었다.

Initial Attempts

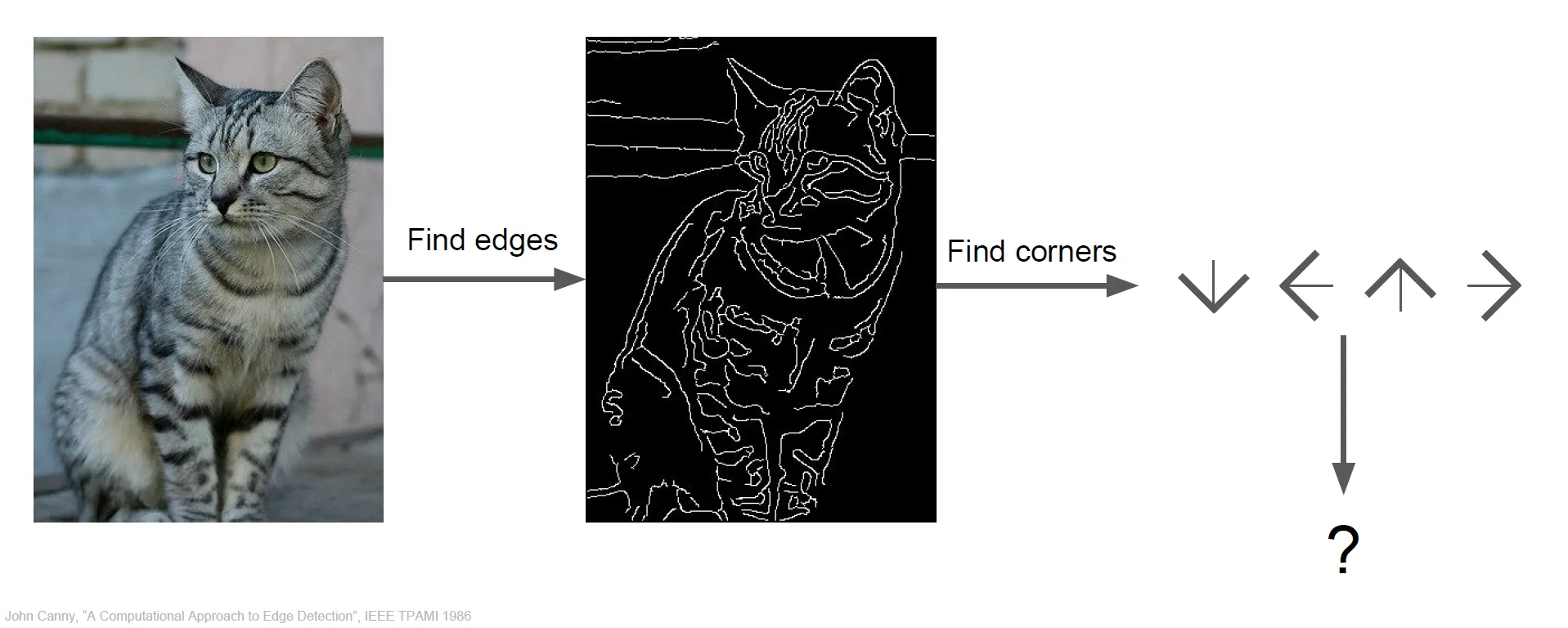
• 이전에 Hubel과 Wiesel의 연구에서 Edge가 중요하다는 사실을 알아냈다.
• 이미지에서 edges를 계산하고 다양한 corners와 edges를 각 카테고리로 분류한다.
  • 귀의 경우 corner 여러개로 구성된다.
  • 이러한 명시적인 규칙 집합을 써내려 가는 방법
• 두가지 문제점
  • 알고리즘이 robust하지 못함
  • 다른 객체를 인식해야한다면 별도로 다시 만들어야함 (확장성이 전혀 없음)

→ 이 세상에 존재하는 다양한 객체들에게 유연하게 적용 가능한 확장성 있는 알고리즘을 만들자.

Data Driven Approach

• 직접 어떤 규칙을 써내려가는 대신에 데이터를 사용하자
  • 이미지와 레이블로 구성된 데이터셋을 수집한다.
  • 머신러닝을 사용하여 Clasifier를 학습한다.
  • 새로운 이미지를 가지고 Classifier를 평가한다.

Nearest neighbor

• 이전과 달리 두 개의 함수로 구성된다.
  • train 함수 : 입력이 이미지와 레이블, 출력은 우리의 모델
  • test 함수 : 입력이 모델이고, 출력은 이미지의 예측값
• Nearest Neighbor의 경우 단순한 Classifier이다.
  • train step : 단지 모든 학습 데이터를 기억한다.
  • test step : 새로운 이미지를 train 이미지를 비교하며 가장 유사한 이미지로 레이블링한다.

CIFAR 10

• 데이터 소개
  • 10가지 클래스 (비행기, 자동차, 새, 고양이 등)
  • 50000개 학습 이미지
  • 10000개 테스트 이미지
• 이러한 이미지에 NN 알고리즘을 적용하면 train set에서 “가장 가까운 샘플”을 찾게된다.
  • 항상 맞지는 않음을 볼 수 있음

→ 그렇다면, 이미지 쌍이 있을때 어떻게 비교를 할까?

Distance Metric to compare images

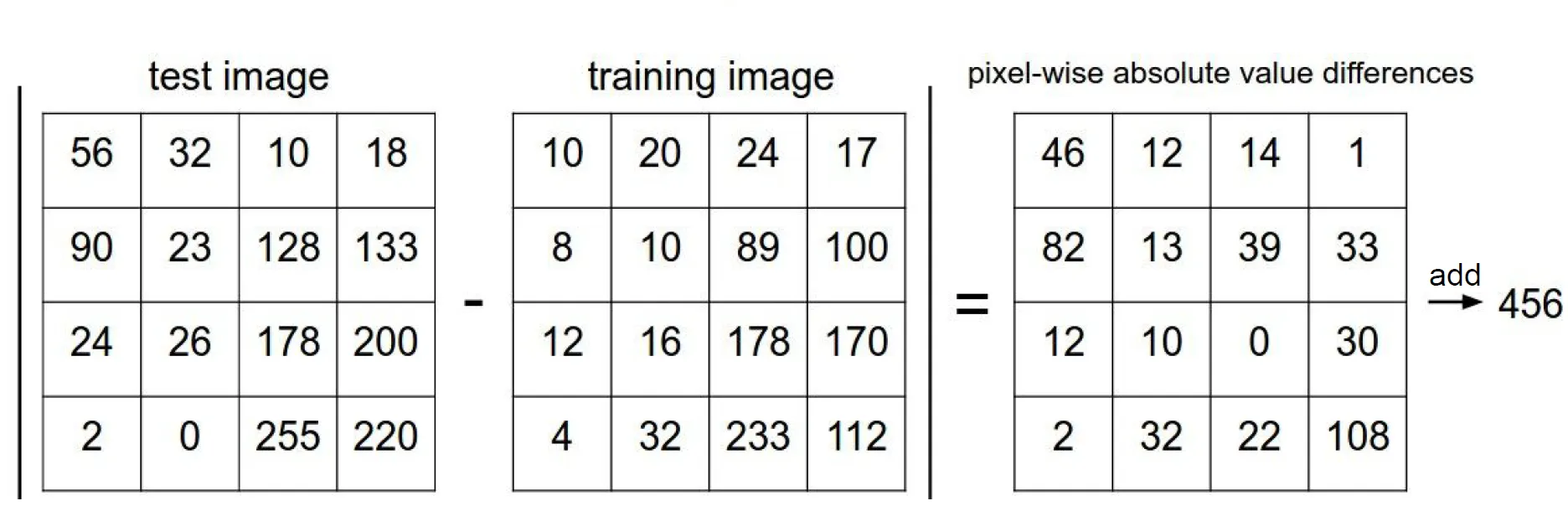
L1 distance

• Manhaton distance라고도 불림
• 이미지의 픽셀 간에 차이의 절대값을 모두 더함

성능 평가

• N개의 이미지가 있다면 학습과 예측 속도가 얼마나 빠를까?
  • train : O(1)
  • test : O(n)

→ 문제점 : 우리는 빠르게 예측하고 느리게 학습하는 것을 원한다.

→ CNN 같은 parametic model은 nn과는 정반대로 train 시간은 오래 걸리고 test 시간은 빠르다.

Decision regions

• 2차원 평면 상의 각 점은 학습 데이터
• 점의 색은 클래스 레이블(카테고리)
• 2차원 평면 내의 모든 좌표에서 각 좌표가 어떤 학습 데이터와 가장 가까운지 계산
• 분류기의 성능이 그닥 좋지 않다.
  • 가운데의 경우 대부분 초록색 점들인데 중간에 노란 점이 끼여있음
  • 초록색 영역이 파란색 영역을 침범하고 있음 (이러한 점은 noise이거나 spurious)

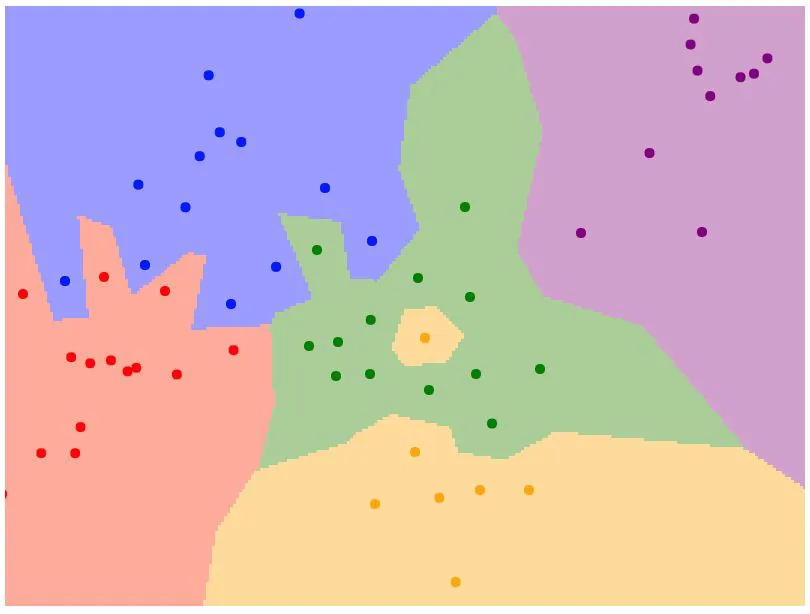
K-Nearest Neighbors

• 이러한 문제를 해결하기 위한 NN의 조금 더 일반화된 버전
• 가장 가까운 이웃을 k개 만큼 찾고 이웃끼리 투표하고 많은 득표수로 예측

→ k를 적어도 1보다는 큰 값을 택하여 decision boundary가 더 부드러워지고 더 좋은 결과를 보이게 할 수 있다.

💡 Computer vision 공부를 할떄는 다양한 관점을 유연하게 다루는 능력이 매우 중요하다.

• 이미지를 고차원 공간에 존재하는 하나의 점이라고 생각
• 반대로 이미지를 이미지 자체로 봄

→ 두 관점을 자유롭게 오갈 수 있는 능력은 아주 유용

K 값 설정

• K-nn을 사용하기 위해 K 값을 결정해야한다.
• 가장 가까운 이웃뿐만 아니라 더 많은 이웃들이 투표에 참여하면(더 높은 K를 설정) 각종 잡음들에 조금 더 robust할 것임을 추측할 수 있다.

Distance Metric

• K-nn을 사용할 때 결정해야 할 한 가지 사항 - metric
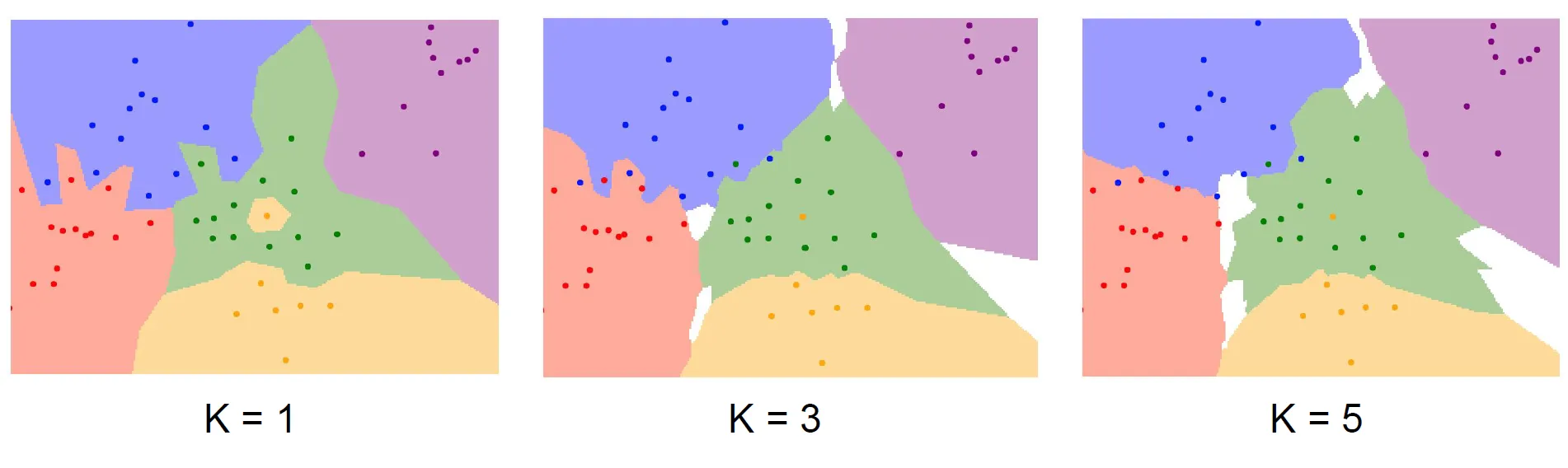
  • L1 Distacne : 픽셀 간 차이 절대값의 합
  • L2 Distance : Euclidean distance, 제곱합의 제곱근
• 서로 다른 척도에서는 해당 공간의 근본적인 기하학적 구조 자체가 서로 다르기 때문에 거리 척도를 정해주는 것이 중요하다.

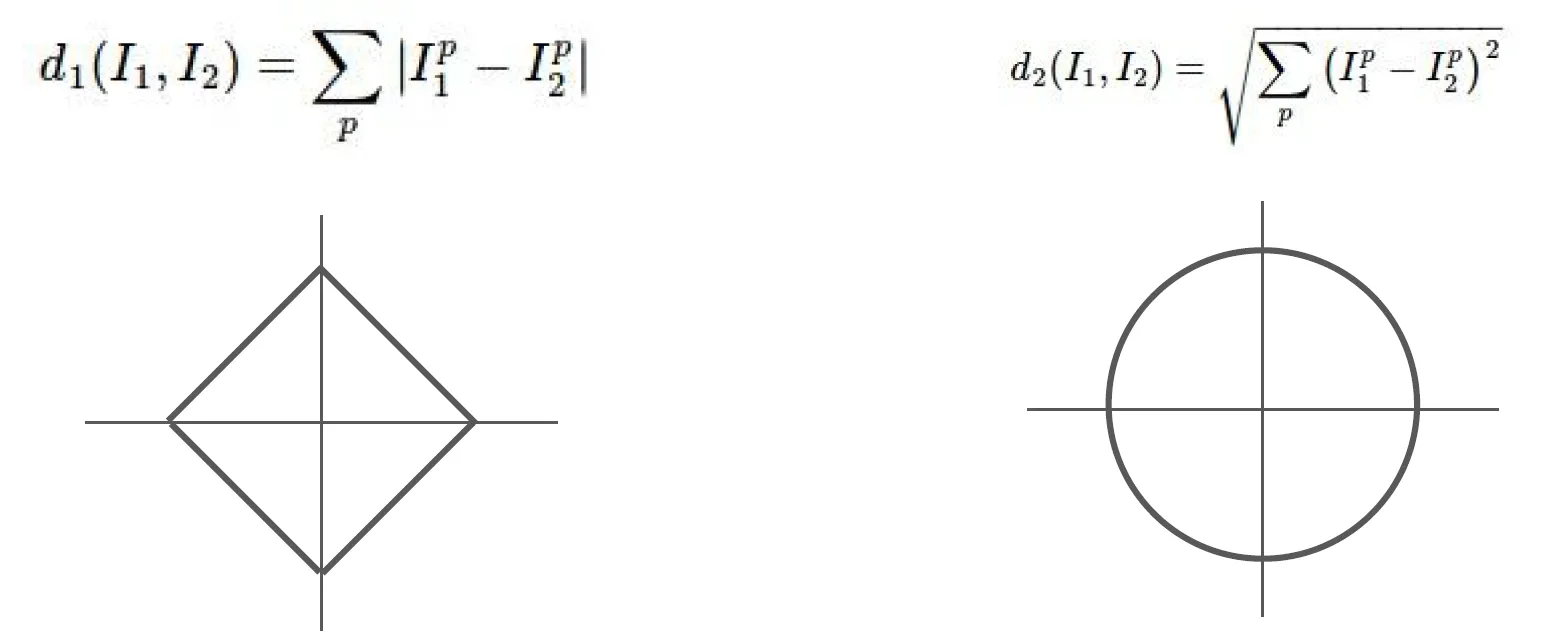
💡 L1 distance vs L2 distance

• L1 distance : 어떤 좌표 시스템이냐에 따라 많은 영향을 받는다. (기존의 좌표계를 회전시키면 L1 distance가 변한다.)
• L2 distance : 반면, 좌표계와 아무 연관이 없다.

→ 특징 벡터의 각 요소들이 개별적인 의미를 가지고 있다면, L1 distance가 더 잘 어울릴 수도 있다. (e.g. 키, 몸무게)
→ 특징 벡터가 일반적인 벡터이고, 요소들간의 실질적인 의미를 잘 모르는 경우라면, L2 distance가 더 잘 어울릴 수도 있다.

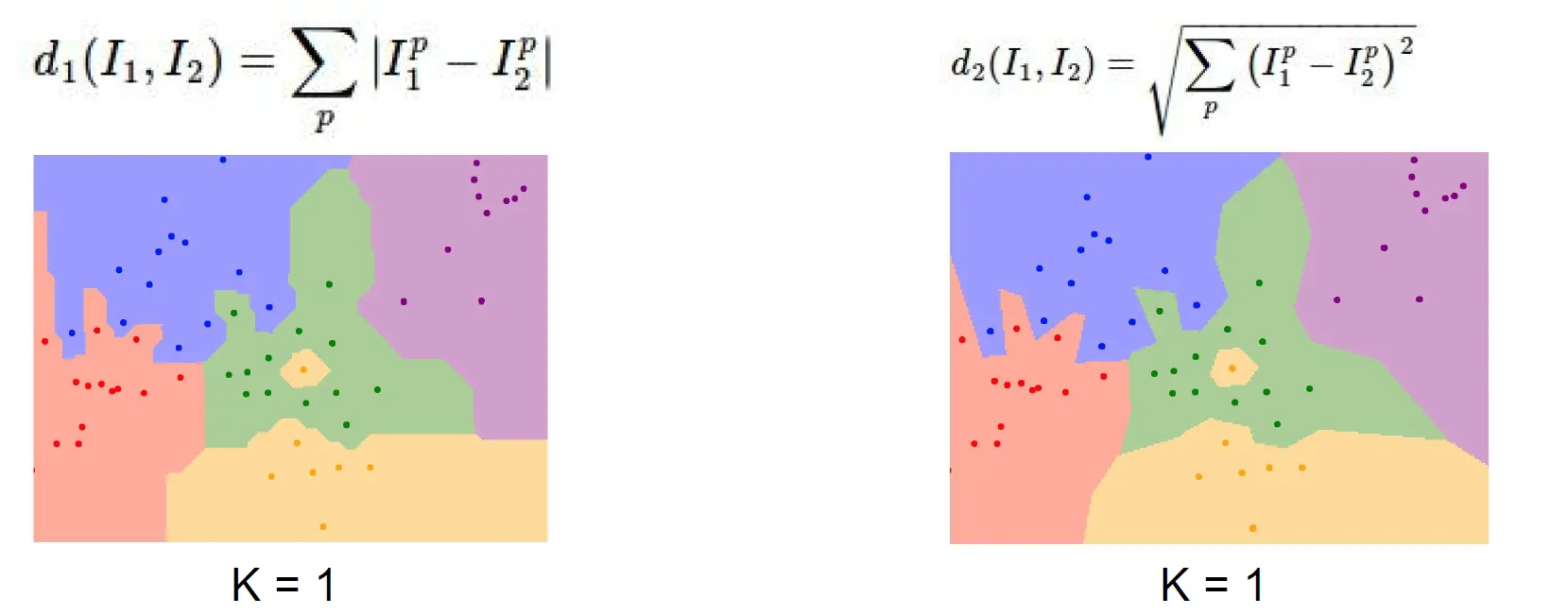
Decision regions

• 거리 척도에 따라 decision boundary의 모양 자체가 달라짐을 알 수 있다.

Hyperparameters

• K와 거리척도와 같이 학습 과정에서 미리 설정해야 하는 매개변수를 말한다.
• 하이퍼파라미터는 trian time에 학습 하는 것이 아니므로 학습 전 사전에 반드시 선택해야한다.
• 어떻게 하이퍼파라미터 값을 설정할까?
  • 문제와 데이터에 맞게 다양한 하이퍼파리미터 값을 시도해 보고 가장 좋은 값을 찾는다.

Setting Hyperparmeters

모든 데이터를 학습 데이터로 사용

• “학습데이터의 정확도와 성능”을 최대화하는 하이퍼파리미터 선택

→ 끔찍한 방법, 학습 데이터에 없던 데이터에 대해서는 좋은 성능을 보일 수 없다.

학습데이터와 테스트 데이터로 분리하여 사용

• 학습 데이터로 다양한 파라미터 값들을 학습 시키고 테스트 데이터에 적용시켜 하이퍼파라미터를 선택하는 방법

→ 또한 끔찍한 방법, “테스트 셋에서만” 잘 작동하는 하이퍼파라미터를 고른 것일 수 있다.

학습데이터와 검증 데이터, 테스트 데이터로 분리하여 사용

• 다양한 하이퍼파라미터로 학습 데이터를 학습시키고 검증 데이터로 검증하여 가장 좋았던 하이퍼파라미터를 선택한다.
• 최종 모델에 테스트 데이터로 평가한다.
• 즉, 검증 데이터 셋에서 가장 좋았던 분류기를 가지고 테스트 데이터에는 “오로지 한번만” 평가

→ 알고리즘이 한번도 보지 못한 데이터에 얼마나 잘 작동해 주는 지를 실질적으로 말해줄 수 있다.

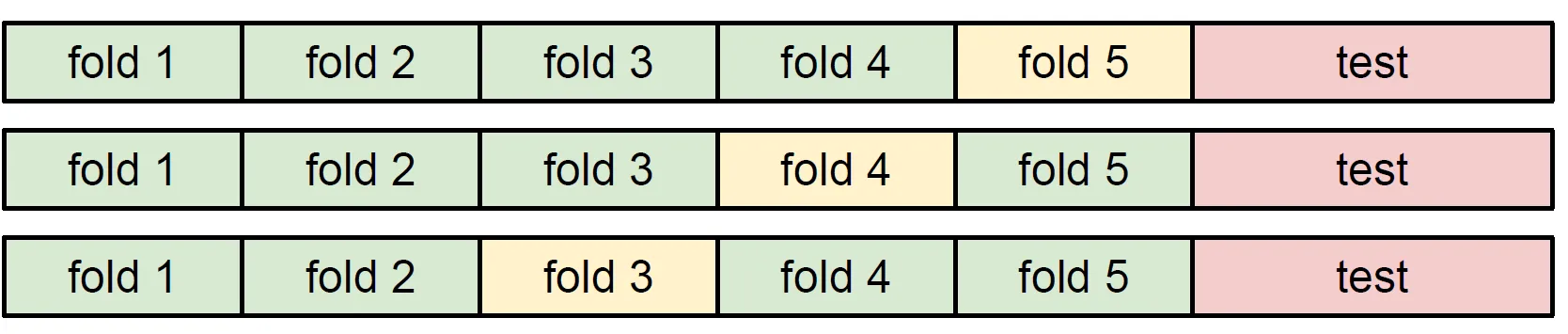
교차검증

• 교차검증 단계
  • 데이터 분할: 데이터를 훈련 세트와 테스트 세트로 나누고, 훈련 세트를 여러 폴드로 분할
  • 훈련 및 검증: 각 폴드마다 훈련하고, 나머지 폴드로 검증하여 모델 성능을 평가
  • 반복: 모든 폴드에 대해 훈련-검증 과정을 반복
  • 최종 평가: 교차검증의 평균 성능을 얻은 후, 테스트 세트를 사용해 최종 성능을 평가

→ 이러한 방식이 거의 표준이지만, 딥러닝 같은 큰 모델을 학습시킬때는 학습 자체의 많은 계산량으로 잘 쓰이지는 않는다.

💡 테스트 데이터가 한번도 보지 못한 데이터를 대표할 수 있는가?

• 기본적 통계학적 가정 : 데이터는 독립적이며 유일한 하나의 분포에서 나온다. (i.i.d assumption

💡 i.i.d assumption

• 다음의 가정을 따르는 것을 의미한다.
  • 독립적(Independent): 각 데이터 샘플은 서로 독립적으로 수집되었으며, 하나의 샘플이 다른 샘플에 영향을 미치지 않음을 의미
  • 동일한 분포(Identically Distributed): 모든 데이터 샘플이 동일한 확률 분포를 따르며, 샘플 간의 분포 차이가 없음을 가정

→ 이러한 가정은 모델이 데이터의 패턴을 정확하게 학습하고 일반화하는 데 중요한 역할을 한다.

• i.i.d 가정을 따르는 경우
  • 랜덤 샘플링: 데이터가 무작위로 수집되었을 때, 즉 샘플이 서로 독립적이고 동일한 확률 분포에서추출되었을 때
  • 동일한 환경에서 데이터 수집: 모든 샘플이 동일한 조건, 시간, 장소 등 동일한 환경에서 수집된 경우
  • 무작위 실험: 실험에서 각 데이터 포인트가 독립적으로 생성되고, 동일한 조건 아래에서 수행되는 경우 (예: 동일한 장비로 반복 측정)

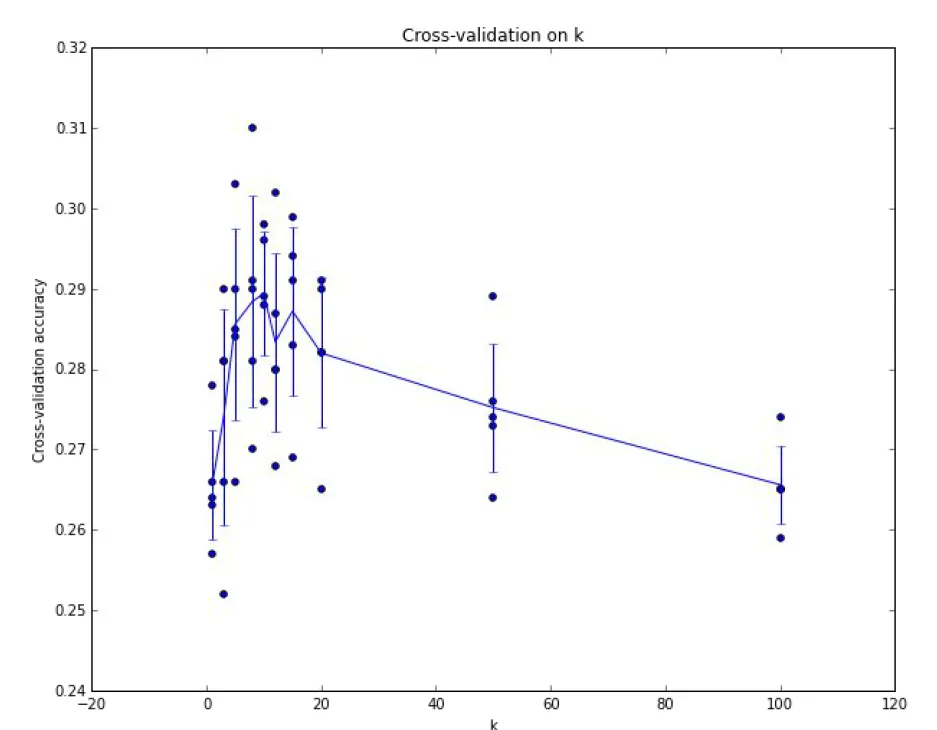
성능 평가

• 각 k마다 5번의 교차 검증 실행
  • line을 통해 여러 검증 fold 별 성능의 분산을 고려해 볼 수 있다.
    • 분산을 계산하면, 어떤 파라미터가 가장 좋은지? 성능의 분산도 알 수 있다.
• 여기서는 k = 7일 경우에 가장 좋은 성능을 보인다.

한계

• 실제로 입력이 이미지인 경우 k-NN Classifier를 잘 사용하지 않는다.
  • K-nn은 너무 느리다.
  • L1/L2 Distance가 이미지 간의 거리를 측정하기에 적절하지 않기 때문이다. (이미지간에 지각적 유사성을 측정하는 척도로는 적절하지 않다)
  • 차원의 저주

차원의 저주

• K-NN이 잘 동작하려면 전체 공간을 조밀하게 커버할 만큼의 충분한 트레이닝 샘플이 필요하다.
• 그렇지 않으면 이웃이 사실은 엄청 멀 수 있어, 테스트 이미지를 제대로 분류할 수 없다.
• 공간을 조밀하게 덮기 위해서는 충분한량의 학습 데이터가 필요한데, 그 양은 차원이 증가함에 따라 기하급수적으로 증가한다.

→ 고차원의 이미지의 경우 모든 공간을 조밀하게 메울만큼의 데이터를 모으는 일은 현실적으로 불가능

Linear Classification

• 아주 간단하지만, Neural network, CNN의 기반 알고리즘이다.
  • 가장 기본이 되는 Linear Classifier를 블럭에 비유한다면,
  • Neural Network를 구축할때, 다양한 컴포넌트를 사용할 수 있는데, 이러한 컴포넌트들을 한데모아 CNN이라는 거대한 타워를 지을 수 있다.
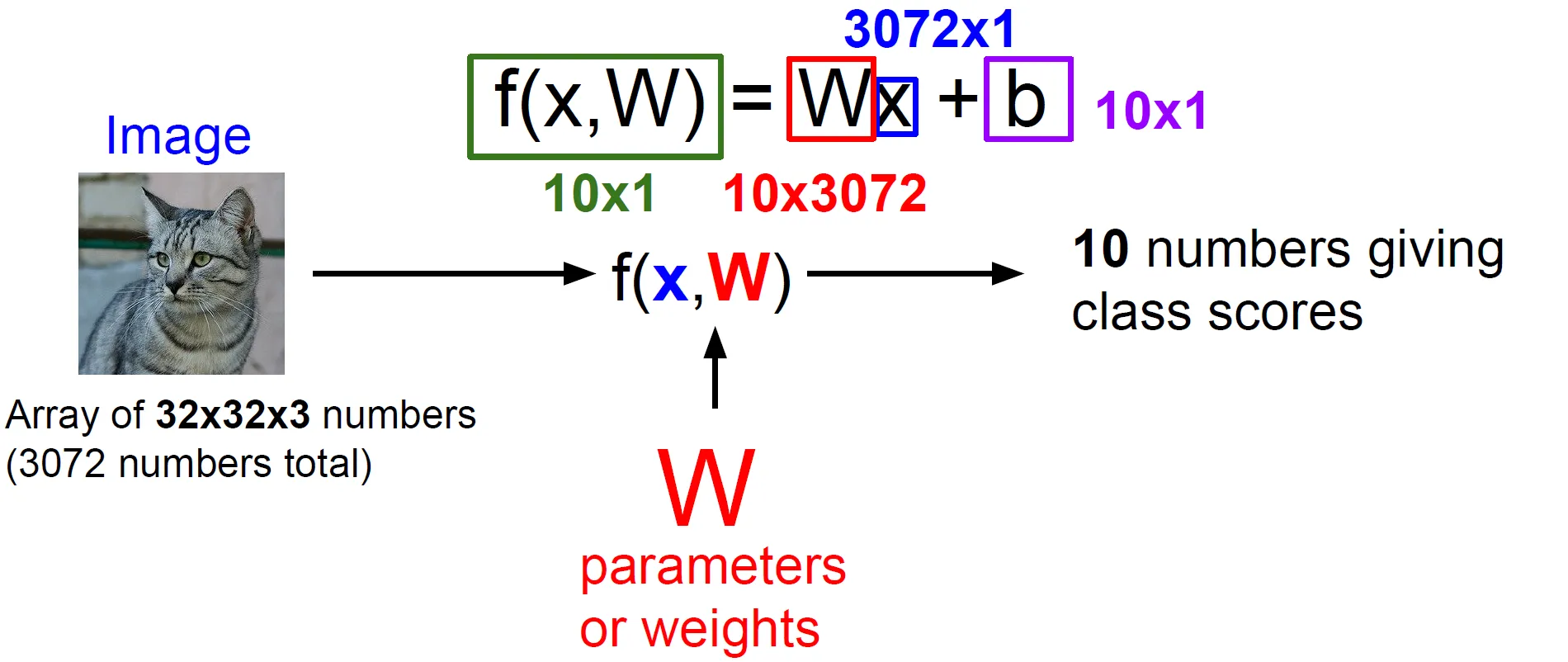
• Linear Classifier는 parametric model의 가장 단순한 형태이다.
  • 데이터 X와 파라미터 W를 가지고 각 카테고리 스코어를 출력한다.
    • 고양이 스코어가 가장 높다면, 입력 X가 “고양이”일 확률이 크다는 것을 의미
• 학습 데이터의 정보를 요약하고 요약된 정보를 파라미터 W에 모아준다.
  • Test time에는 더 이상 학습 데이터가 필요없이 파라미터 W만 있으면 된다.

→ 딥러닝은 함수 F의 구조를 적절하게 설계하는 일이다.

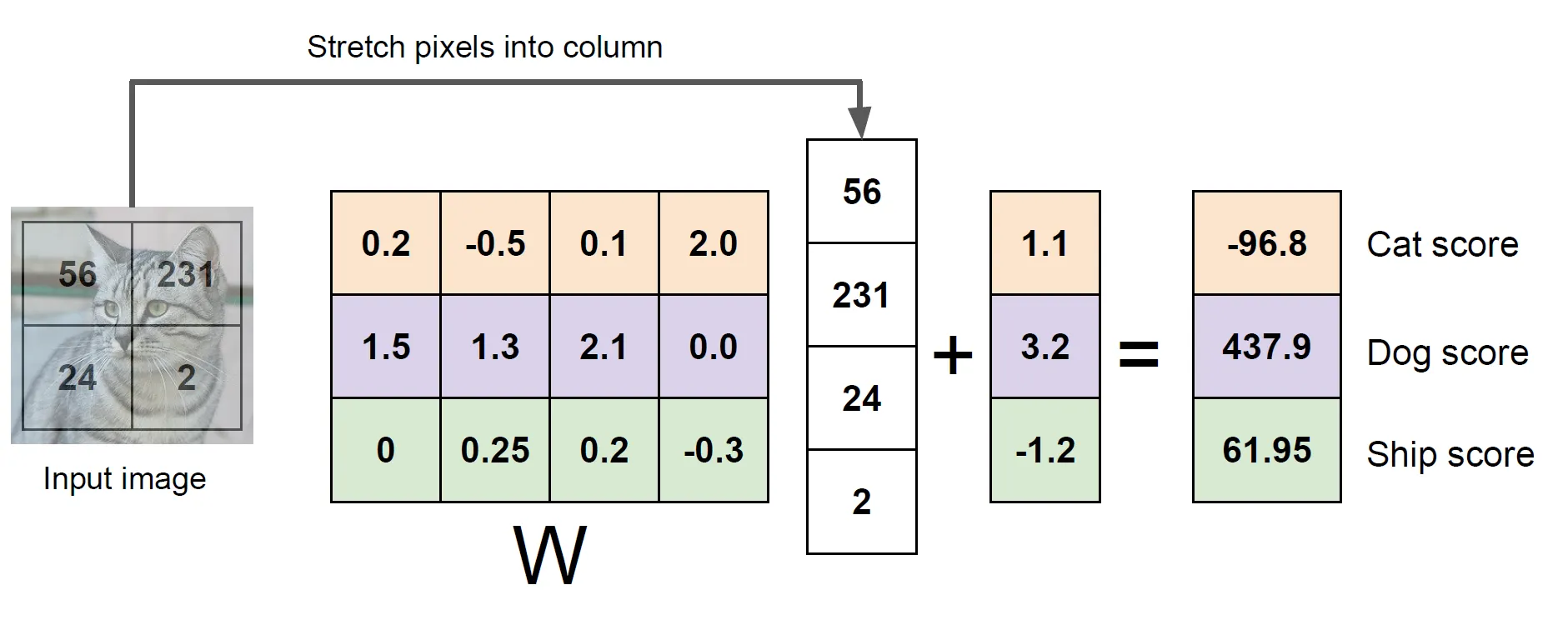
연산 예시

• 4 pixel의 이미지를 3개의 클래스(고양이, 개, 배) 중 하나로 분류하는 문제
• 연산 과정
  • 2 x 2 이미지를 4-dim 열 벡터로 쭉 편다.
  • 4 x 3 가중치 행렬을 곱해주고 bias는 데이터와 독립적으로 각 카테고리에 연결된다.

→ 즉, 입력 이미지의 픽셀 값들과 가중치 행렬을 내적한 값에 bias term을 더한 것이다.

💡 Linear clasification은 특정한 패턴(템플릿) 매칭과 거의 유사함

• 가중치 행렬 W의 각 행은 각 이미지에 대한 템플릿으로 볼 수 있다.
• 이러한 행 벡터와 이미지의 열벡터 간의 내적을 계산
  • 여기서 내적은 클래스 간 템플릿의 유사도를 측정하는 것과 유사함

💡 템플릿이란?

• 특정 클래스의 특징을 잘 표현하는 패턴 또는 기준 형태를 의미
• 선형 분류기에서 템플릿은 가중치 행렬 W의 행 벡터로 표현
  • 이러한 벡터는 특정 클래스가 가질 법한 이미지의 특징(예: 모양, 색상, 패턴 등)을 수치적으로 나타낸 것

Linear classifier 해석

템플릿 매칭 관점에서 이해

• 각 카테고리에 대해 하나의 템플릿을 학습
• 가중치 행렬 w의 한 행을 뽑아서 이미지로 시각화
  • 한 클래스 내에 다양한 특징들이 존재할 수 있으나, 모든 것들을 평균화시키므로 다양한 모습들이 있더라도 각 카테고리를 인식하기 위한 템플릿은 단 하나만 존재한다.
  • 즉, Linear classifier가 클래스 당 하나의 템플릿 밖에 허용하지 않기 때문이다.

→ 하지만 Neural Network같은 복잡한 모델은 클래스 당 하나의 템플릿만 학습 할 수 있다는 것과 같은 제약조건이 없으므로 조금 더 정확도 높은 결과 기대 가능하다.

이미지를 고차원 공간의 한 점으로 보는 것

• Linear Classifier는 각 클래스를 구분시켜 주는 선형 결정 경계를 그어주는 역할

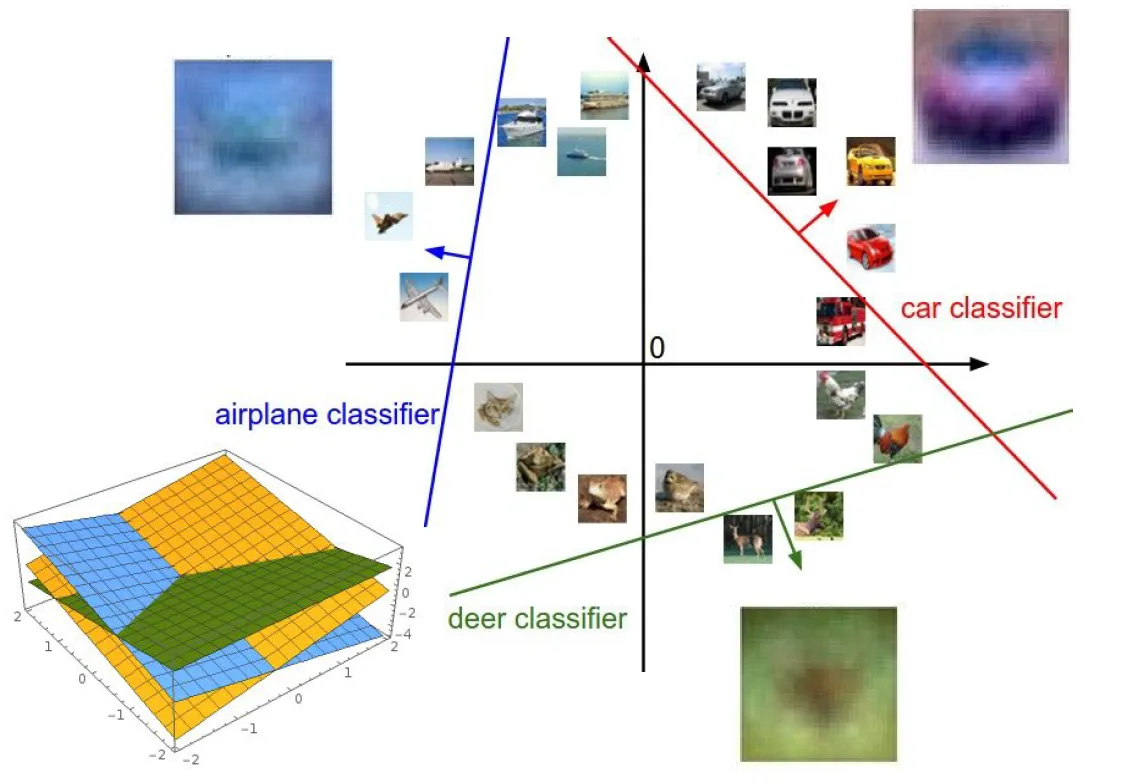
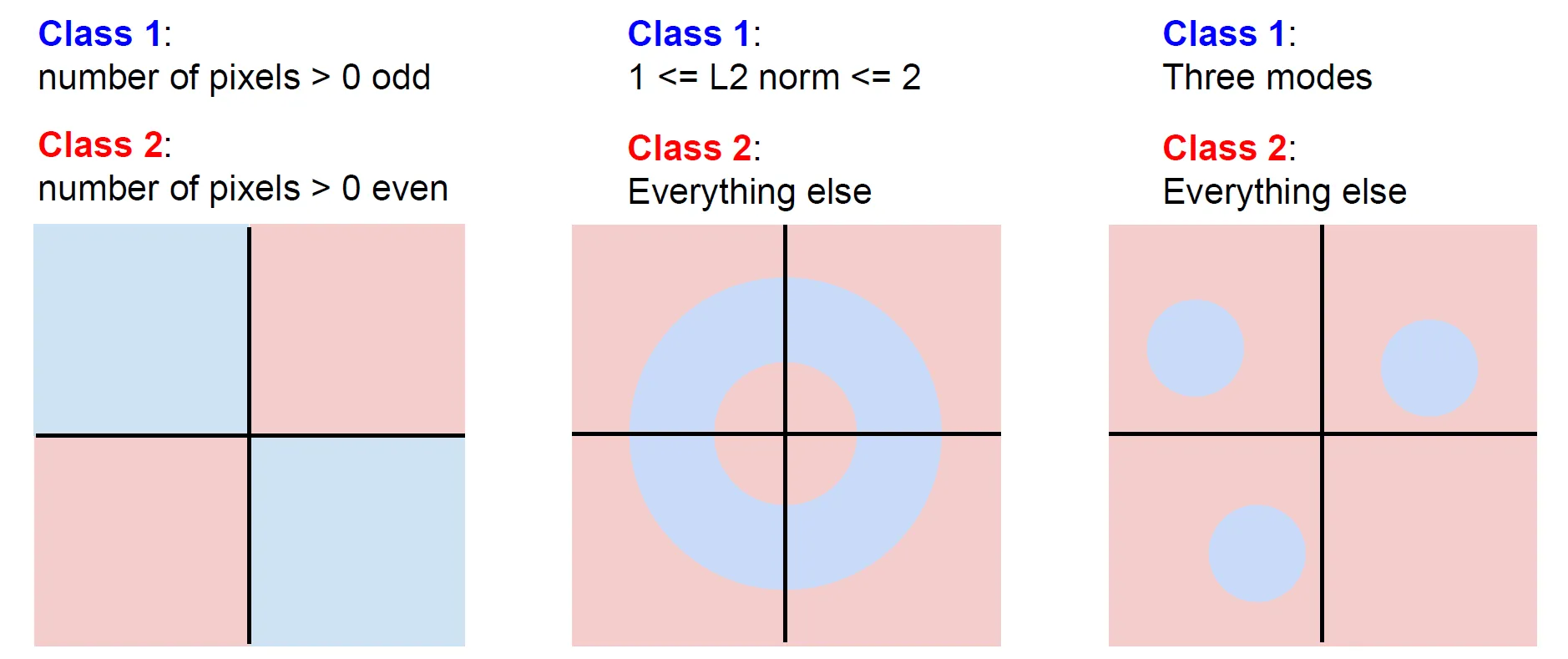
Linear classifier로 풀기 어려운 문제

• 다음 이미지의 문제들은 decision boundary를 긋기 어려움