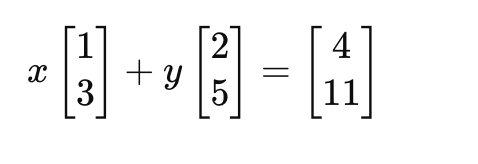[Linear Equation] Solution Sets of Linear System

Homogeneous Linear Systems

• Ax = 0 의 형태로 나오게 되는 형태의 식
  (모든 항이 0인 선형 방정식)
  -> 항상 최소한 하나의 해를 갖는다 : x = 0

(trivial solution) : 자명한 해

!trivial solution -> nontrivial solution (0말고도 해가 더 있는 경우)

: if and only if the equation has at least one free variable일때 존재
-> 자유 변수가 있을때 존재

ex1) Determine whether there is a nontrivial solution

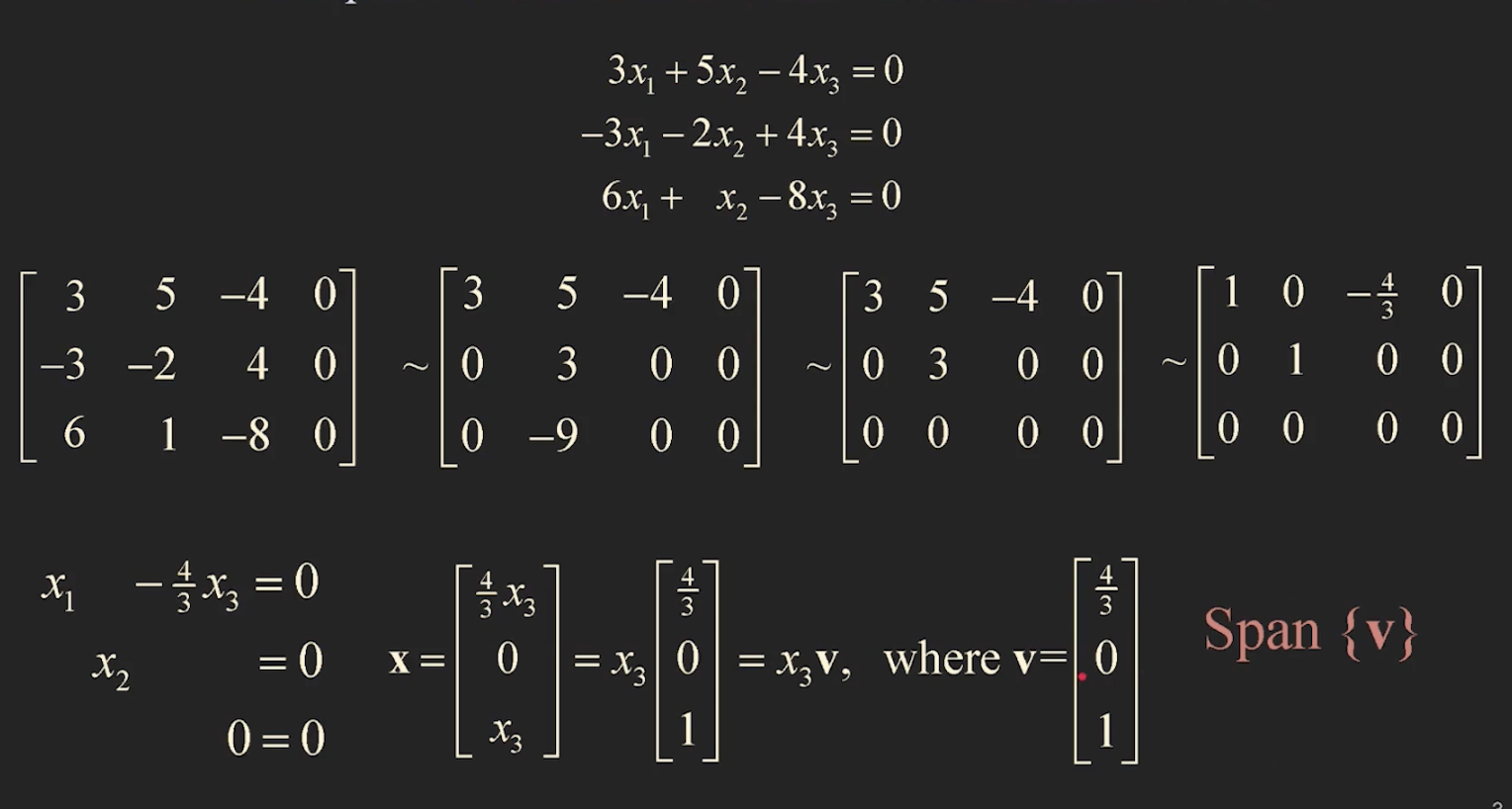
• 헷갈려서 계속 다시 정리 하는 정의..

연립 일차방정식 = 벡터끼리의 합
x+2y=4
3x+5y=11
이 연립방정식을
이런식으로 표현하는 것이 선형 결합(linear combination)
즉, 해를 구하는것은 ->
벡터를 잘 조합해서 목표 위치(우변 벡터)를 맞추는 것

행렬

행렬 A × 벡터 x = 벡터 b

• 행렬 = 여러 개의 벡터 묶음
• 벡터 x = 각각 몇 배 할지 정하는 숫자
  즉, 행렬은 벡터들을 한꺼번에 처리하는 도구로 이 예제에서 이해할 수 있다.

조건:
선형 시스템 𝐴𝑥=𝑏 가 consistent (즉, 해가 최소한 하나 이상 존재)하다고 가정하자.
그리고 그 해 중 하나를 𝑝 라고 하자.

결론:
이 방정식의 전체 해집합은 다음과 같이 표현된다:
w=p+𝑣ℎ
여기서 𝑣ℎ는 동차(homogeneous) 방정식 𝐴𝑥=0 의 임의의 해이다.

구분	Homogeneous Equation	Nonhomogeneous Equation
형태	$Ax = 0$	$Ax = b$, $b \neq 0$
의미	"오직 0벡터"가 항상 해인 구조	상수 벡터 $b$에 의해 결과가 0이 아님
해의 존재	항상 최소한 $x = 0$ (자명해) 존재	해가 존재할 수도 있고 없을 수도 있음 (조건 필요)
해의 집합	벡터공간 (서브스페이스)	벡터공간이 아님. 한 점을 중심으로 하는 평면(아핀 공간)

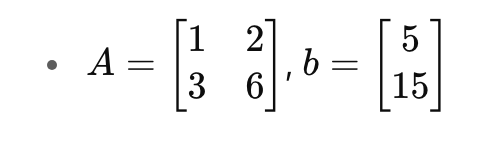
비동차 방정식 Ax = b는 어떤 특정한 해 p ->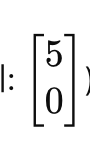
을 가질 수 있다.
이때 전체 해집합은 다음과 같이 표현된다:
x=p+𝑣ℎ
여기서, 𝑣ℎ는 Ax = 0의 해이다.

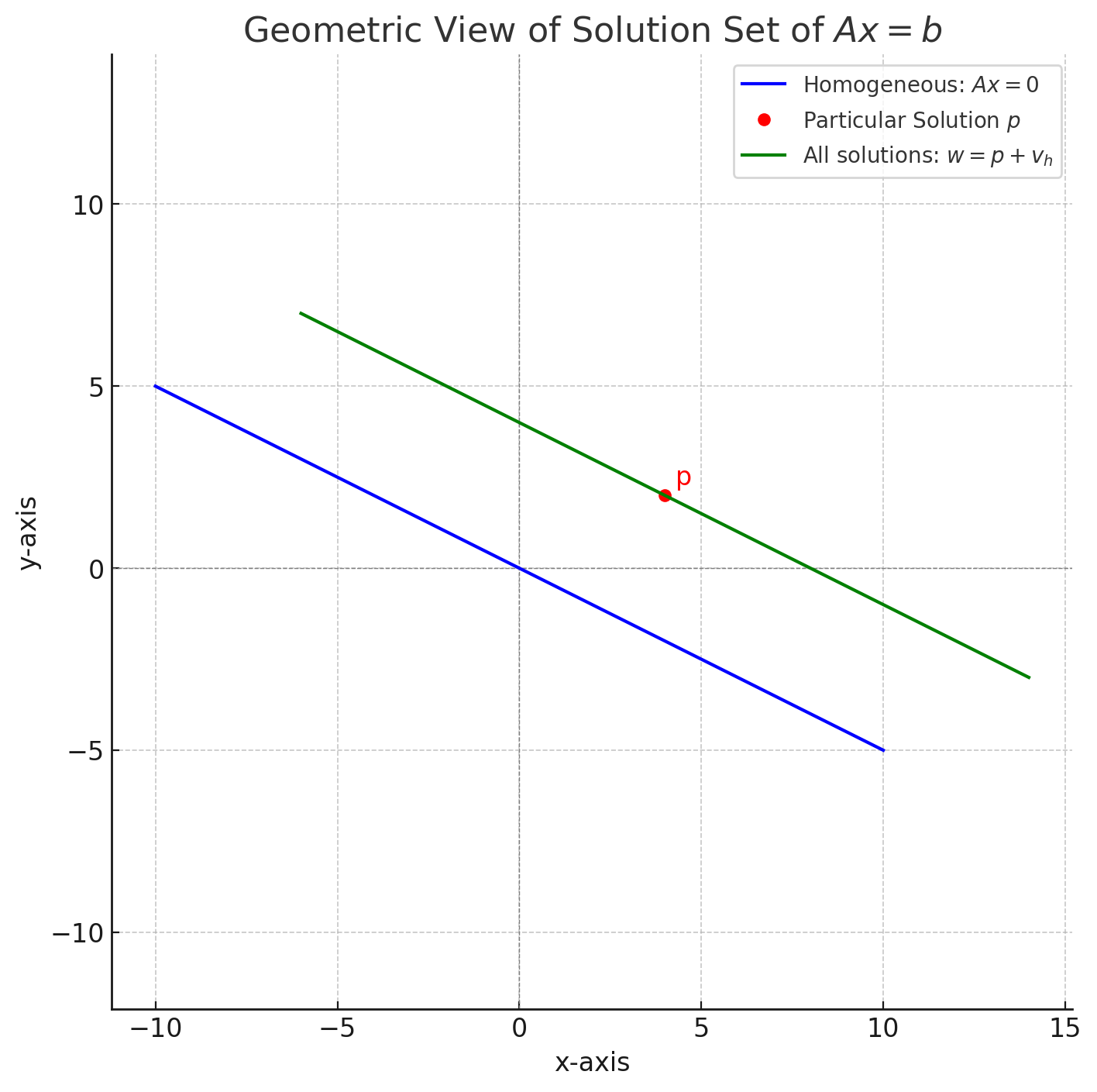
비동차 해 집합 = 동차 해 집합 + 특정한 한 해