[Linear Equation] The Matrix Equations Ax = b

Ax

• Ax: product of A and x

A의 열 개수 = x의 행 개수

Ax = x₁a₁ + x₂a₂ + ⋯ + xₙaₙ

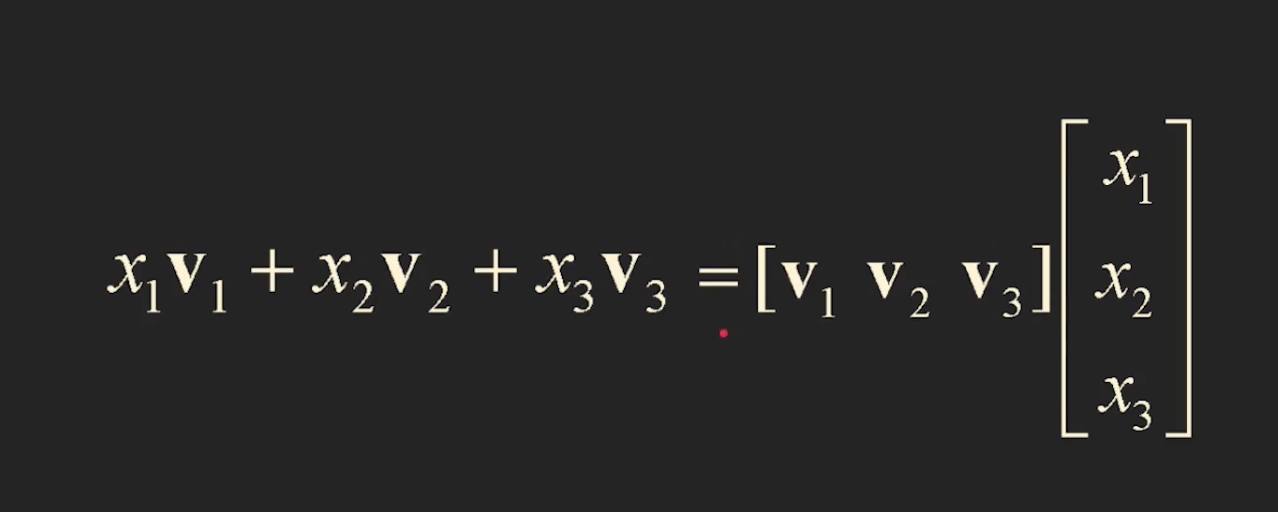
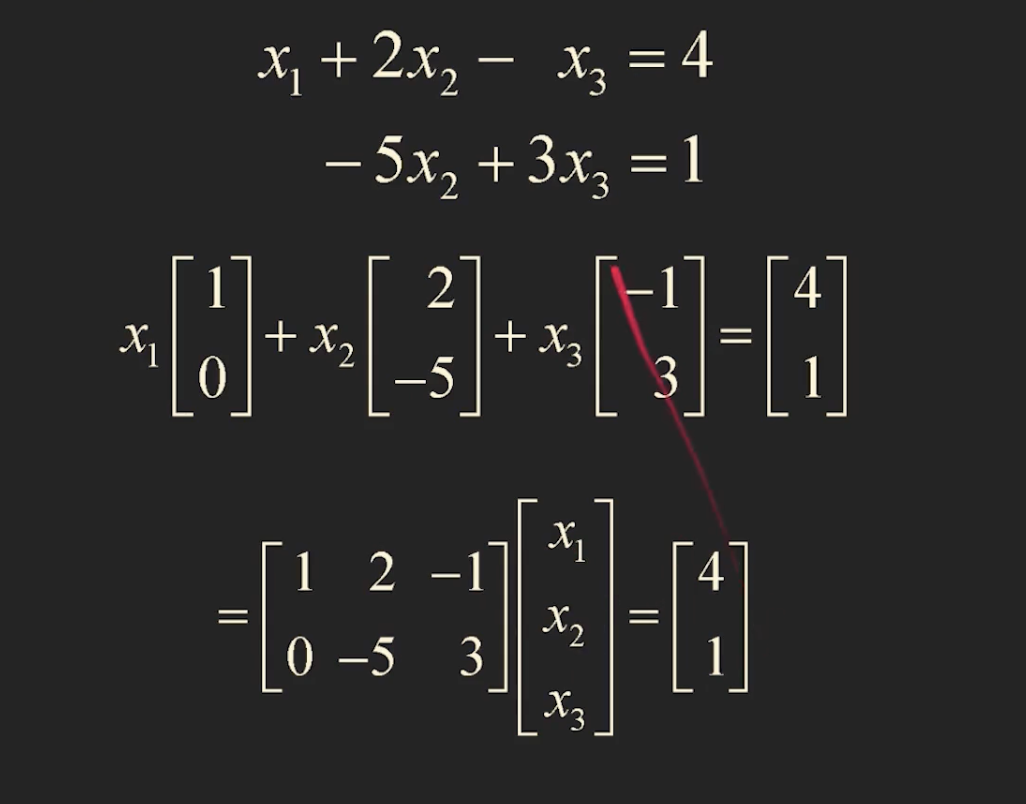
• 이런식으로 표현 할 수 도 있음

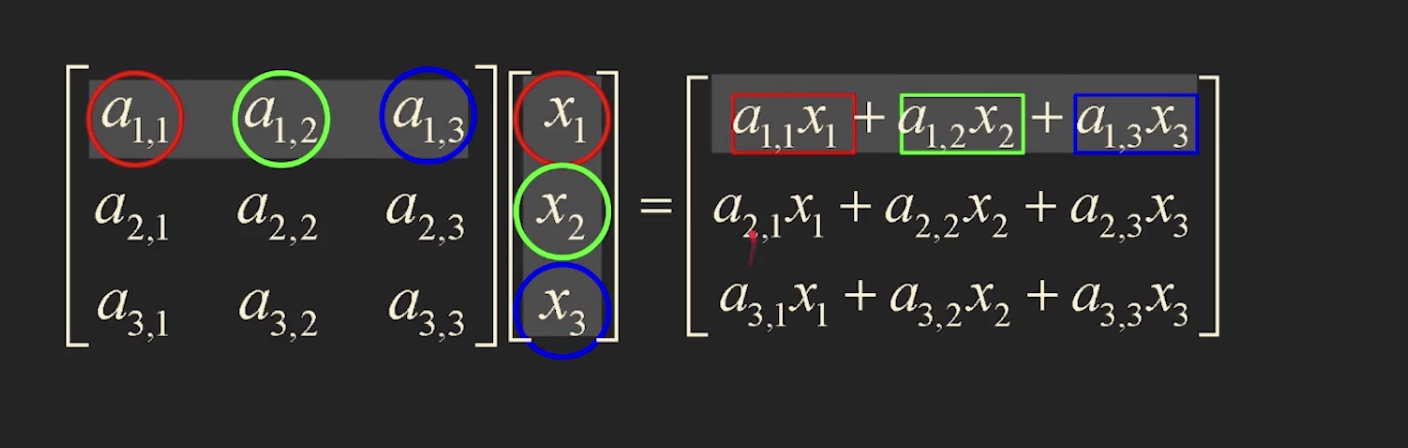
효율적인 방식으로 계산하는 방법 ->

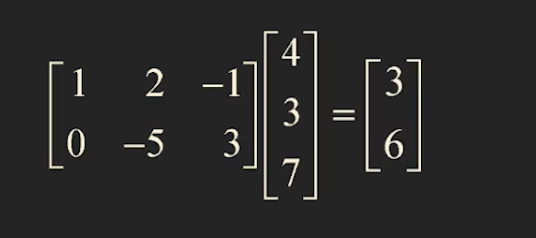
위의 방식을 통해 빨리 계산 가능

identity matrix I

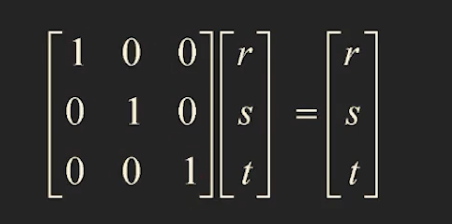
이름	수식 표현	의미 요약
Matrix Equation	$A\vec{x} = \vec{b}$	행렬 곱으로 표현한 연립방정식
Vector Equation	$x_1a_1 + x_2a_2 + \cdots + x_n a_n = b$	벡터들의 선형결합으로 표현
Augmented Matrix	([a1 a2 ... an b])	행렬로 해 구하기 쉽게 만든 행렬

조건 a

For each b in 𝑅𝑚, 𝐴𝑥=𝑏 has a solution.

조건 b

Each 𝑏 ∈ 𝑅𝑚 is a linear combination of the columns of 𝐴

조건 a를 벡터 조합 관점에서 본 표현.
→ "Ax = b"가 풀린다는 건 "b를 a₁, a₂, ..., aₙ으로 만들 수 있다"는 말과 같다

조건 c

The columns of 𝐴 span 𝑅𝑚

“A의 열벡터들로 𝑅𝑚 의 어떤 벡터든 만들 수 있다" = span이 전체 공간이다.

조건 d

A has a pivot position in every row