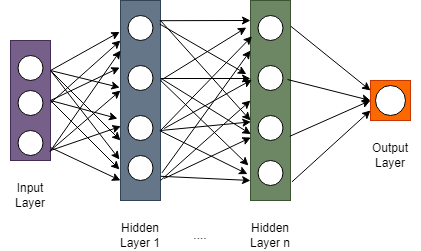
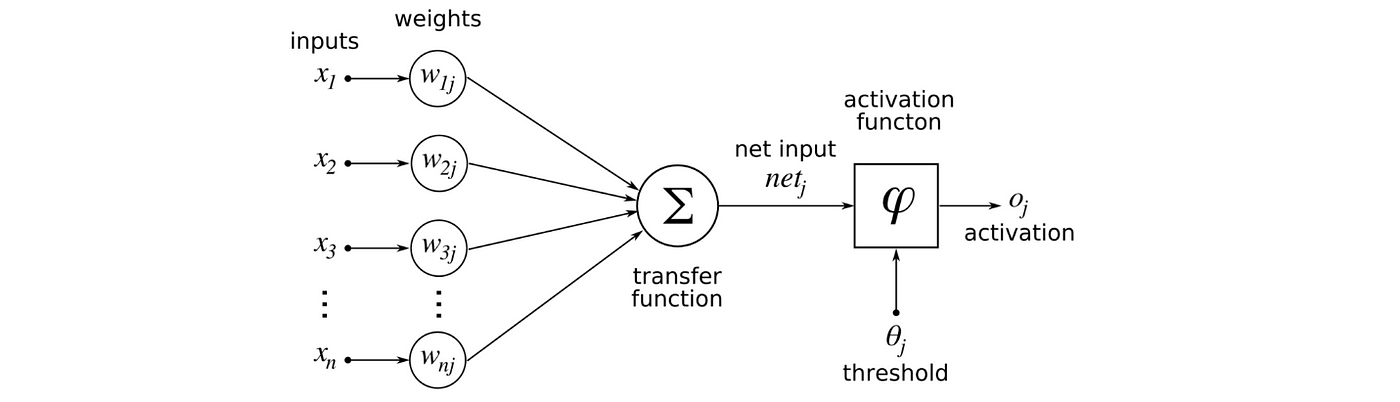
Activation Function? 🔥활성화 함수(Activation Function) 는 심층 신경망(Deep Neural Network, DNN)에서 은닉층의 레이어를 활성화해주기 위해 사용되는 함수이다.
이러한 활성화 함수에는 ReLU, Sigmoid, tanh 등 다양하게 존재하고, 이들의 공통점은 선형적이지 않은 비선형적 함수라는 것이다.
Why Non-Linear?
🧐 왜 활성화 함수가 선형 함수이면 안되는 걸까?
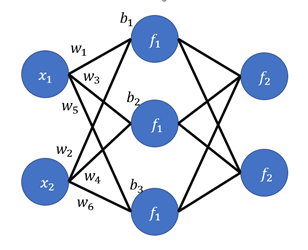
x → = [ x 1 x 2 ] \overrightarrow{x} = \begin{bmatrix}x_1\\x_2\\ \end{bmatrix} x = [ x 1 x 2 ] W 1 = [ w 1 w 2 w 3 w 4 w 5 w 6 ] W_1 = \begin{bmatrix}w_1&w_2\\w_3&w_4\\w_5&w_6 \end{bmatrix} W 1 = ⎣ ⎢ ⎡ w 1 w 3 w 5 w 2 w 4 w 6 ⎦ ⎥ ⎤ b 1 → = [ b 1 b 2 b 3 ] \overrightarrow{b_1} = \begin{bmatrix}b_1\\b_2\\b_3 \end{bmatrix} b 1 = ⎣ ⎢ ⎡ b 1 b 2 b 3 ⎦ ⎥ ⎤
이를 바탕으로 첫 번째 Hidden layer의 값은 아래와 같다.
W 1 x → + b 1 → = [ w 1 w 2 w 3 w 4 w 5 w 6 ] [ x 1 x 2 ] + [ b 1 b 2 b 3 ] = [ x 1 w 1 + x 2 w 2 + b 1 x 1 w 3 + x 2 w 4 + b 2 x 1 w 5 + x 2 w 6 + b 3 ] W_1\overrightarrow{x}+\overrightarrow{b_1} = \begin{bmatrix}w_1&w_2\\w_3&w_4\\w_5&w_6 \end{bmatrix}\begin{bmatrix}x_1\\x_2\\ \end{bmatrix}+\begin{bmatrix}b_1\\b_2\\b_3\end{bmatrix}=\begin{bmatrix}x _{1} w _{1} +x _{2} w _{2} +b _{1} \\x _{1} w _{3} +x _{2} w _{4} +b _{2} \\x _{1} w _{5} +x _{2} w _{6} +b _{3}\end{bmatrix} W 1 x + b 1 = ⎣ ⎢ ⎡ w 1 w 3 w 5 w 2 w 4 w 6 ⎦ ⎥ ⎤ [ x 1 x 2 ] + ⎣ ⎢ ⎡ b 1 b 2 b 3 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ x 1 w 1 + x 2 w 2 + b 1 x 1 w 3 + x 2 w 4 + b 2 x 1 w 5 + x 2 w 6 + b 3 ⎦ ⎥ ⎤
첫 번째 Hidden Layer에서 다음 Layer로 넘어가기 전 활성화 함수 f 1 f_1 f 1
f 1 ( [ x 1 w 1 + x 2 w 2 + b 1 x 1 w 3 + x 2 w 4 + b 2 x 1 w 5 + x 2 w 6 + b 3 ] ) f_1(\begin{bmatrix}x _{1} w _{1} +x _{2} w _{2} +b _{1} \\x _{1} w _{3} +x _{2} w _{4} +b _{2} \\x _{1} w _{5} +x _{2} w _{6} +b _{3}\end{bmatrix}) f 1 ( ⎣ ⎢ ⎡ x 1 w 1 + x 2 w 2 + b 1 x 1 w 3 + x 2 w 4 + b 2 x 1 w 5 + x 2 w 6 + b 3 ⎦ ⎥ ⎤ )
지금의 방식과 똑같이 적용하면 두 번째 Layer에서 다음 Layer로 전달되는 값은f 2 ( W 2 f 1 ( [ x 1 w 1 + x 2 w 2 + b 1 x 1 w 3 + x 2 w 4 + b 2 x 1 w 5 + x 2 w 6 + b 3 ] ) + b 2 → ) f_2(W_2f_1(\begin{bmatrix}x _{1} w _{1} +x _{2} w _{2} +b _{1} \\x _{1} w _{3} +x _{2} w _{4} +b _{2} \\x _{1} w _{5} +x _{2} w _{6} +b _{3}\end{bmatrix})+\overrightarrow{b_2}) f 2 ( W 2 f 1 ( ⎣ ⎢ ⎡ x 1 w 1 + x 2 w 2 + b 1 x 1 w 3 + x 2 w 4 + b 2 x 1 w 5 + x 2 w 6 + b 3 ⎦ ⎥ ⎤ ) + b 2 )
그런데 이때 만약 활성화 함수 f 1 f_1 f 1 f 2 f_2 f 2 y = x y=x y = x
그러면 위의 식은
W 2 [ x 1 w 1 + x 2 w 2 + b 1 x 1 w 3 + x 2 w 4 + b 2 x 1 w 5 + x 2 w 6 + b 3 ] + b 2 → = W 2 ( W 1 x → + b 1 → ) + b 2 → = W 2 W 1 x → + W 2 b 1 → + b 2 → W_2\begin{bmatrix}x _{1} w _{1} +x _{2} w _{2} +b _{1} \\x _{1} w _{3} +x _{2} w _{4} +b _{2} \\x _{1} w _{5} +x _{2} w _{6} +b _{3}\end{bmatrix}+\overrightarrow{b_2} = W_2(W_1\overrightarrow{x}+\overrightarrow{b_1})+\overrightarrow{b_2}=W_2W_1\overrightarrow{x} + W_2\overrightarrow{b_1}+\overrightarrow{b_2} W 2 ⎣ ⎢ ⎡ x 1 w 1 + x 2 w 2 + b 1 x 1 w 3 + x 2 w 4 + b 2 x 1 w 5 + x 2 w 6 + b 3 ⎦ ⎥ ⎤ + b 2 = W 2 ( W 1 x + b 1 ) + b 2 = W 2 W 1 x + W 2 b 1 + b 2
W 2 W 1 W_2W_1 W 2 W 1 W W W W 2 b 1 → + b 2 → W_2\overrightarrow{b_1}+\overrightarrow{b_2} W 2 b 1 + b 2 b → \overrightarrow{b} b
W x → + b → W\overrightarrow{x}+\overrightarrow{b} W x + b
해당 식은 마치 W W W b → \overrightarrow{b} b 실질적으로는 하나의 Layer를 거친 것 과 다르지 않다는 것이고, 이는 우리가 MLP에서 Multi-Layer를 설계한 근본적인 이유가 반영되지 않았다는 것이다. 꼭 y = x y=x y = x y = a x + b y=ax+b y = a x + b
따라서 MLP에서 Multi_Layer를 살리기 위해서는 활성화 함수가 비선형적 함수 이어야 한다.
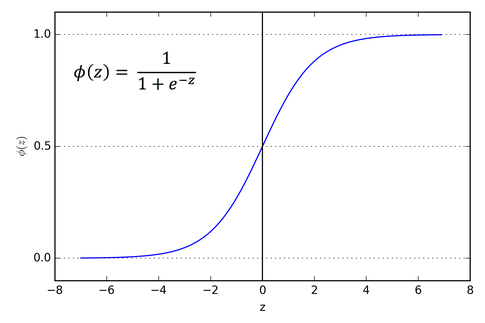
Sigmoid
🙆♂️ 장점
Step Function에 비해 정보 손실이 적다
어떤 입력 값에도 항상 0과 1사이의 연속적인 값을 반환하여 확률로 해석이 가능하다
전 구간에서 미분이 가능하므로 역전파 계산이 가능하다
바이너리 분류 문제에 사용 가능하다
🙅♂️ 단점
기울기 소실 문제가 발생할 수 있다
함숫값의 중심이 0이 아니기에 학습이 잘 안될 수도 있다 (zigzag 문제)
exp 연산으로 인해 학습 속도가 느려질 수 있다
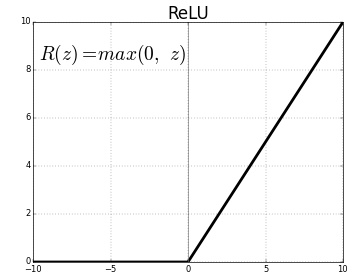
ReLU(Rectified Linear Unit)
현재 딥러닝에서 가장 널리 사용되는 활성화 함수 중 하나이다.
🙆♂️ 장점
기울기 소실 문제가 완화된다
학습 속도가 매우 빠르다
양수에서 포화(saturation)가 발생하지 않는다
🙅♂️ 단점
함숫값의 중심이 0이 아니기에 학습이 잘 안될 수도 있다 (zigzag 문제)
일부 뉴런에서 0만 출력하는 문제가 발생하기도 한다
x x x