Machine Learning

🤖 기계학습은 기계가 스스로 데이터 속의 규칙성을 학습해 패턴을 발견하는 알고리즘이다.

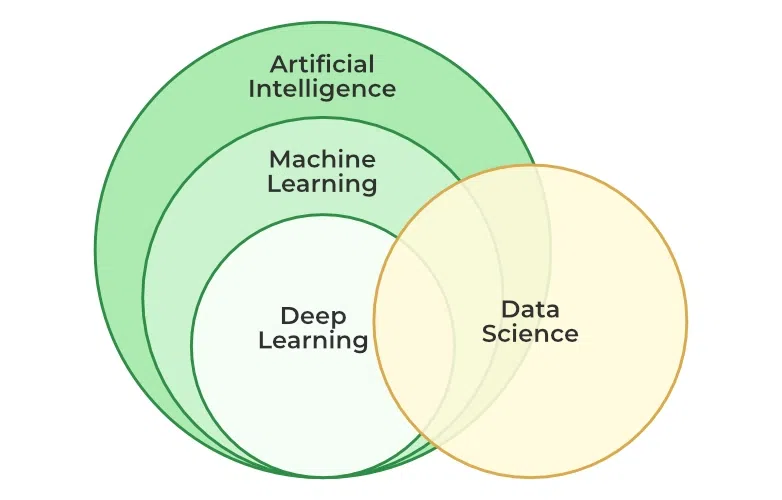
우리가 흔히 말하는 머신러닝, 딥러닝은 인공지능이라는 큰 범주에 포함된 개념으로, 인공지능을 구현하기 위한 방법이라고 생각하면 된다. 특히 딥러닝은 기계학습의 인공신경망이라는 방법론에서 진화한 기술로, 신경망을 여러 계층 쌓아 만들어 'Deep' Learning이라고 한다.

데이터 분석 과정은 크게 [ 문제 정의 => 데이터 수집 및 전처리 => EDA => 모델링 => 평가 ] 의 과정을 거치는데, '모델링' 과정에 기계학습이 사용된다.

기계학습은 크게 아래의 세 가지로 분류된다.

📖 지도 학습(Supervised Learning)은 데이터의 레이블을 기반으로 패턴을 학습하고 예측하는 방법이다.
이는 선생이 학생에게 구몬 학습지(데이터)와 정답지(레이블)을 모두 주고 잘 학습해보라고 하는 것과 같다.
지도학습의 대표적인 방법으로는 분류(Classification), 회귀(Regression)가 있다.

☕ 비지도 학습(Unsupervised Learning)은 데이터의 레이블 없이 데이터의 특성 분포를 파악하는 방법이다.
이는 선생이 학생에게 답안지(레이블)를 주지 않고 학습지(데이터)만 준 뒤 알아서 공부하라고 하는 것과 같다.
비지도 학습의 대표적인 방법으로는 군집화(Clustering), 차원 축소(Demesion Reduction)가 있다.

🎮 강화 학습(Reinforcement Learning)은 기계가 주어진 환경 내에서 보상을 최대화하는 행동을 선택하는 방법이다.
간단히 말해 기계가 잘하면 당근🥕을, 못하면 채찍🩼을 주는 것이다.

Unsupervised Learning

🧐 정답이 없는데 어떻게 학습하고, 어떻게 맞혀요,,,?

Clustering

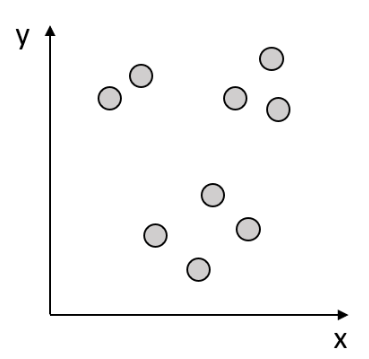
위와 같은 데이터 분포가 존재하고 우리는 해당 데이터 셋을 세 개의 그룹으로 묶어야 한다.
그렇다면 우리는 당연하게도 아래와 같이 그룹을 지을 것이다.

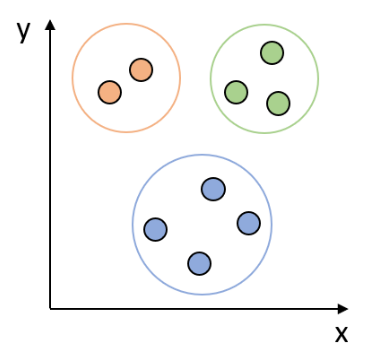
이렇게 우리는 정답, 즉 레이블 없이 데이터의 특성 분포를 파악할 수 있다.

하지만 정답이 존재하지 않으므로 아래와 같이 빨간색으로 표시한 데이터를 어디로 분류해야 하는지에 대한 정답도 없다. 다만 데이터에 대한 특성들이 더 존재한다면 지금보다 더 확실하게 구분할 수 있을 것이다.

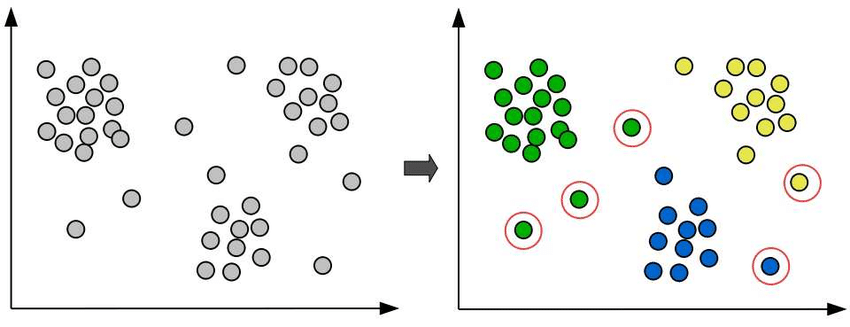
이처럼 데이터의 특성들을 바탕으로 데이터의 그룹을 만드는 것을 군집화(Clustering)이라고 한다.
군집화의 대표적인 방법으로는 K-Means, KNN 등이 있다.

K-Means

🎈 K-Means는 데이터를 K개의 클러스터로 묶는 방법이다.

K-Means 과정은 다음과 같다.

---

1. K개의 점을 랜덤하게 선택한다.
2. 선택한 점을 중심점(Centroid)로 설정하고, 데이터들을 가장 가까운 중심점을 기준으로 할당한다.
3. 각 군집 내의 데이터들의 평균점을 새로운 중심점으로 갱신한다.
4. 중심점이 더 이상 갱신되지 않을 때까지 2~3단계를 반복한다.

---

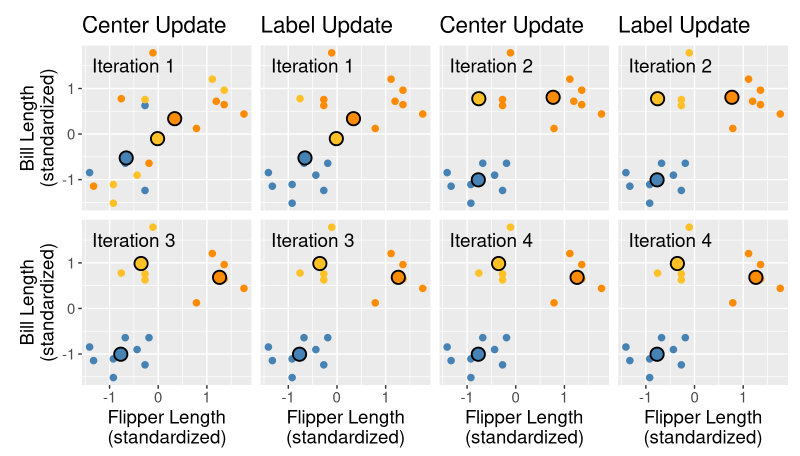
반복 횟수가 늘어날수록 중심점이 적절한 군집의 중심으로 찾아가는 것을 볼 수 있다.

🙆‍♂️ 장점

• 직관적으로 이해할 수 있다
• 연산 속도가 빠르다
• 수렴성이 보장된다

🙅‍♂️ 단점

• 군집의 개수를 직접 설정해야 한다
• 범주형 데이터에는 활용하기 어렵다
• 노이즈와 이상치에 민감하다
• 초기 중심점에 대한 의존도가 높다

DBSCAN

👥 DBSCAN(Density-Based Spatial Clustering of Applications with Noise)은 밀도를 기반으로 군집을 나누는 방법이다.

DBSCAN의 과정은 다음과 같다.

---

1. 주어진 거리 범위(Epsilon) 내에서 포인트를 찾는다
2. 최소 포인트 개수를 만족한다면 해당 포인트를 Core Point로 설정한다
3. 거리 범위 내의 포인트 중에서 포인트를 새로 설정하고 1~2의 과정을 반복한다
4. 거리 범위 내에서 최소 포인트 개수를 충족하지 못한다면 Border Point로 지정한다
5. 모든 포인트에 대해서 1~4 과정을 반복한다
6. 어느 클러스터에도 포함되지 않는 포인트는 Noise Point로 처리한다
   

---

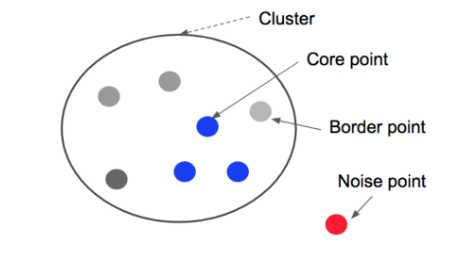
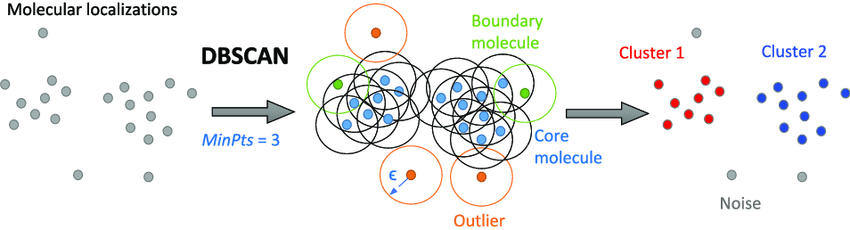
이처럼 DBSCAN을 시행할 경우 가까이 뭉쳐있는 데이터 포인트끼리 하나의 군집을 이루게 된다.

🙆‍♂️ 장점

• 다양한 클러스터를 식별할 수 있다
• 이상치에 대응이 가능하다
• 군집 개수를 지정할 필요가 없다
• 안정적인 클러스터가 도출된다

🙅‍♂️ 단점

• 고차원 데이터에서 활용이 어렵다 (차원의 저주)
• 데이터의 밀도가 일정하지 않을 경우 제대로 군집화가 안된다
• 하이퍼 파라미터에 민감하다
• 클러스터의 경계가 모호하다

Demension Reduction

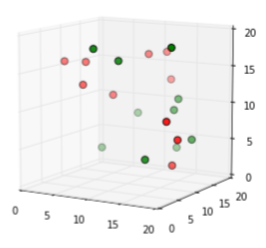
위와 같은 3차원의 데이터를 분석하는 것은 2차원보다는 당연히 복잡할 것이다. 그러나 우리가 앞으로 분석하게 될 데이터들은 3차원을 훌쩍 뛰어넘는 고차원의 데이터들이다😨
우리가 고차원의 데이터를 분석하는 것이 어렵기에 데이터의 특성을 최대한 반영한 채로 차원을 낮춰 분석하는데, 이것을 차원 축소(Demension Reduction)라고 한다.

추가적으로 차원이 늘어날수록 데이터의 밀도가 낮아지게 되고, 이에 따라 모델의 성능이 급격하게 저하될 수 있다. 이를 차원의 저주(The Curse of Demensionality)라고 하며, 차원 축소는 차원의 저주를 막기 위해서도 사용된다.

차원 축소의 방법에는 PCA, t-SNE 등이 있다.

PCA

🔨 PCA(Principal Component Analysis)는 데이터의 정보를 최대한 보존하는 축에 데이터를 투영(Projection)하여 차원을 축소하는 방법이다.

다음은 PCA의 과정이다.

---

1. 데이터 표준화하기
2. 표준화한 데이터의 공분산 행렬 구하기
3. 공분산 행렬의 eigenstuff(eigenvector, eigenvalue) 구하기
4. eigenstuff를 eigenvalue가 큰 것부터 작은 순서대로 정렬하기
5. 원하는 차원만큼의 상위 eigenvector만을 가지고 데이터를 투영하기
   

---

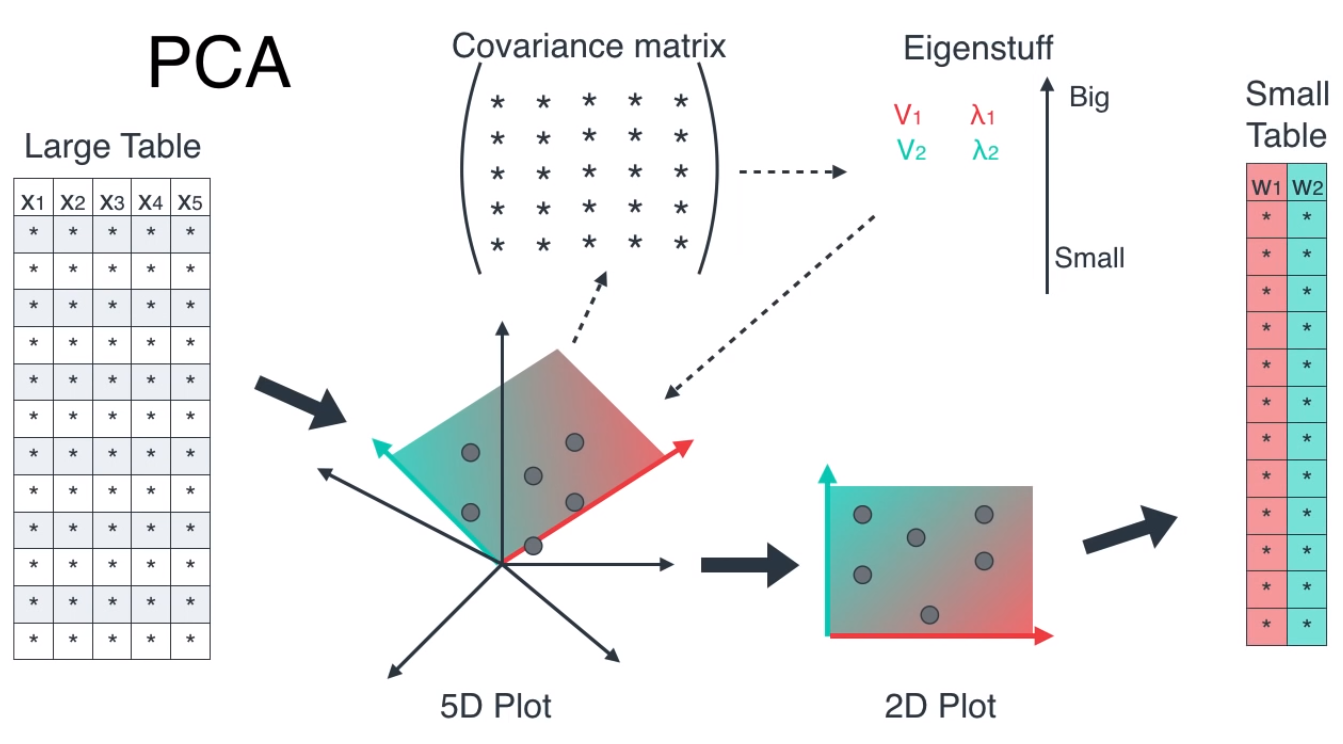
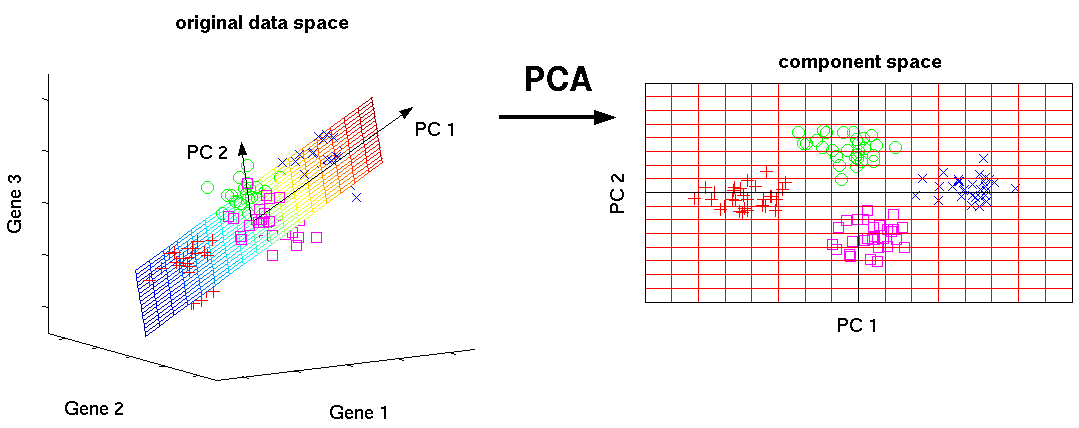
복잡한 3차원의 데이터를 2차원으로 PCA를 통해 차원 축소하였더니 데이터의 분포를 분석하기 더 쉬워졌다.

🙆‍♂️ 장점

• 차원 축소를 통한 직관적인 시각화 가능
• 데이터 압축
• 노이즈 제거 가능

🙅‍♂️ 단점

• 비선형적 데이터에 적합하지 않음
• 정보 손실로 인한 성능 저하 가능성 있음
• 데이터 축이 달라져 결과 해석에 어려움 있을 수도 있음

Practice

🧌 포켓몬 데이터를 분석해보자!

https://pokemondb.net/pokedex/all
위 사이트는 포켓몬 데이터를 정리해놓은 아주 좋은 사이트다.

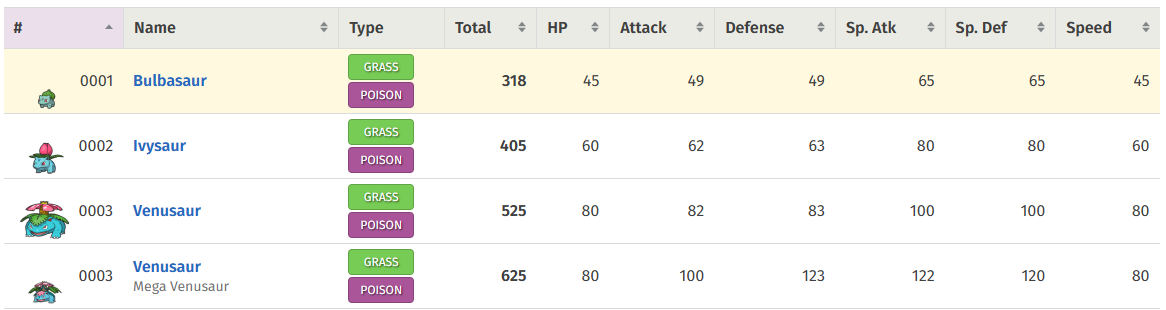
해당 사이트에서 포켓몬 데이터를 불러와 데이터 프레임으로 나타낸다.

from bs4 import BeautifulSoup
import requests
import pandas as pd
from io import StringIO # table을 Data Frame으로 바꿔줌

html = requests.get("https://pokemondb.net/pokedex/all").text
soup = BeautifulSoup(html, 'html_parser')

html_table = soup.find('table')
html_table_str = str(html_table)
html_table_io = StringIO(html_table_str)

df = pd.read_html(html_table_io)[0] #표를 리스트 형태로 반환하므로 인덱싱을 해야 함
print(df)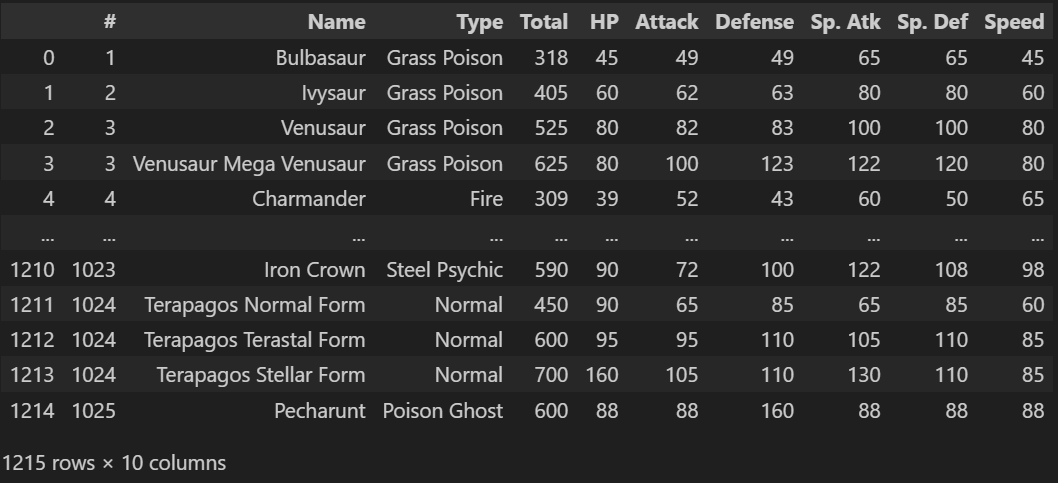

야무지게 잘 됐다😎,,,고 생각했지만 Type 컬럼을 보면 타입이 두 개인 포켓몬은 'Grass Poison'과 같이 하나의 문자열로 되어있다. 이는 데이터를 분석할 때 정확한 분석을 방해하므로 타입을 분리해야 한다.

type_ = df['Type'].str.split()
df['Type_1'] = type_.str[0]
df['Type_2'] = type_.str[1]

print(df.info())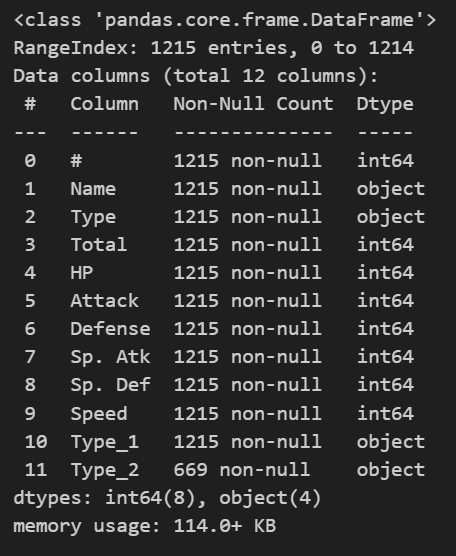

다시 데이터를 보면 타입이 잘 분리된 것을 볼 수 있다. Type_2에 Null 값이 발생한 것은 모든 포켓몬이 타입을 두 개 갖고 있는 것이 아니기 때문이다.

이제 데이터를 시각화하여 나타내보자.

import matplotlib.pyplot as plt
import seaborn as sns

type_list = list(en_df['Type_1'].unique())

plt.figure(figsize = (10,3), dpi=150)
plt.xticks(rotation=45, ha = 'right')
sns.boxplot(x = 'Type_1', y = 'Total', data = en_df, order = type_list)
plt.show()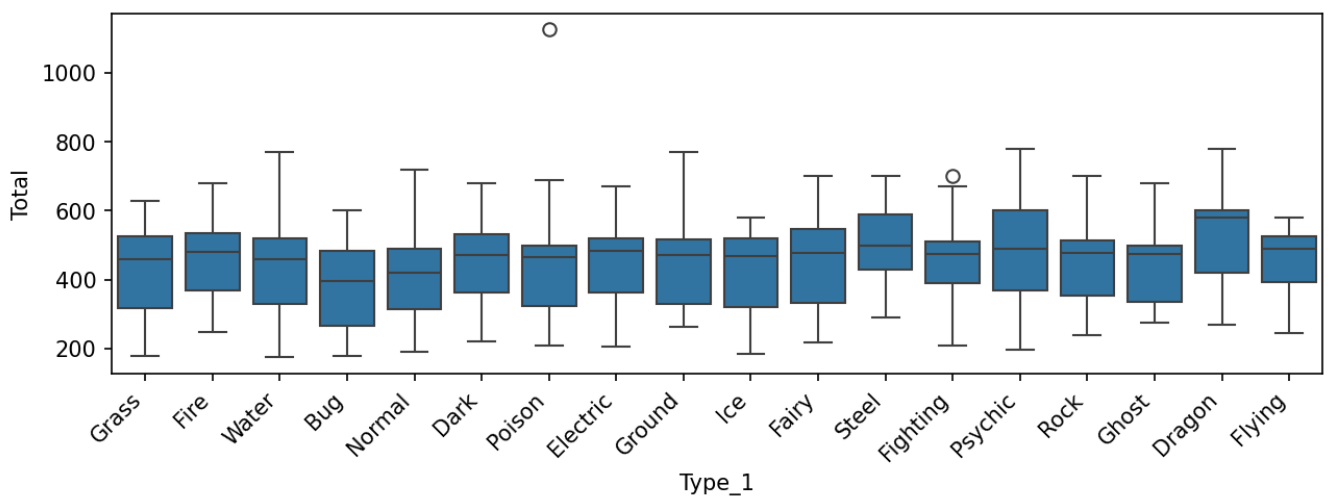

가로 축을 Type_1, 세로 축을 Total로 했을 때의 Box Plot이다. 독타입에 존재하는 괴랄한 이상치를 제외하고 데이터가 대체적으로 균등하게 분포되어 있는 것 같다.

저 괴랄한 이상치 포켓몬을 찾아보니 Eternatus라는 무한다이노라는 포켓몬이라고 한다,, 저런 밸런스 붕괴 포켓몬이 존재해도 되는건가,,,

plt.figure(figsize = (10,3), dpi=150)
plt.xticks(rotation=45, ha = 'right')
sns.boxplot(x = 'Type_2', y = 'Total', data = df, order = type_list)
plt.show()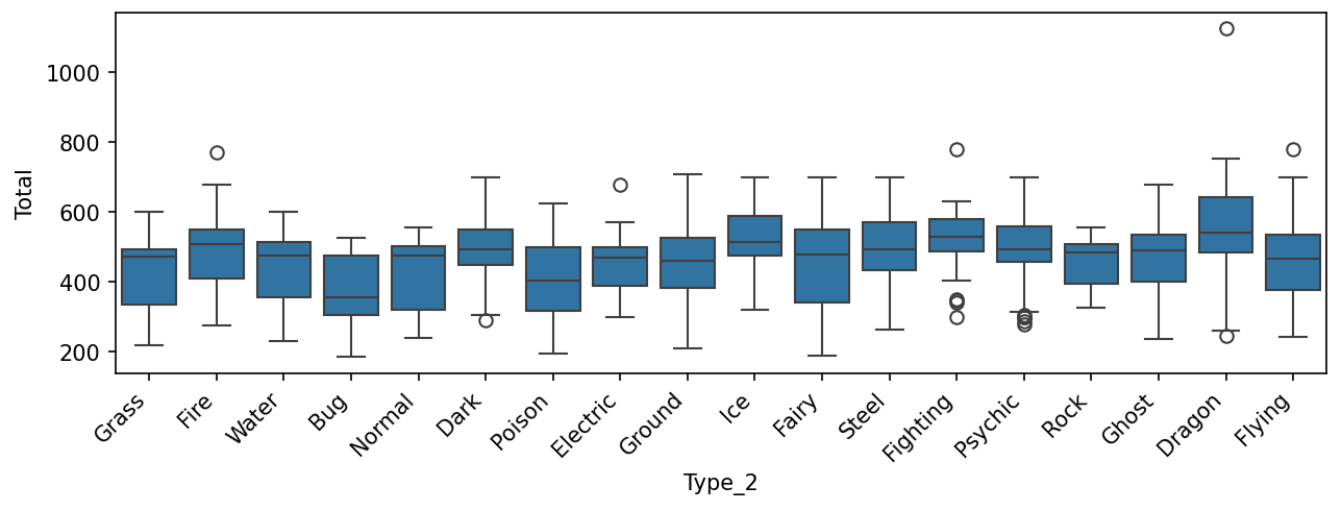

Type_2도 메가 어쩌구 빼고는 비슷비슷하게 분포되어 있는 듯 하다.

이번엔 모든 능력치 데이터의 Scatter Plot과 히스토그램을 봐보자.

sns.pairplot(df[['HP', 'Attack', 'Defense', 'Sp. Atk', 'Sp. Def', 'Speed']])
plt.show()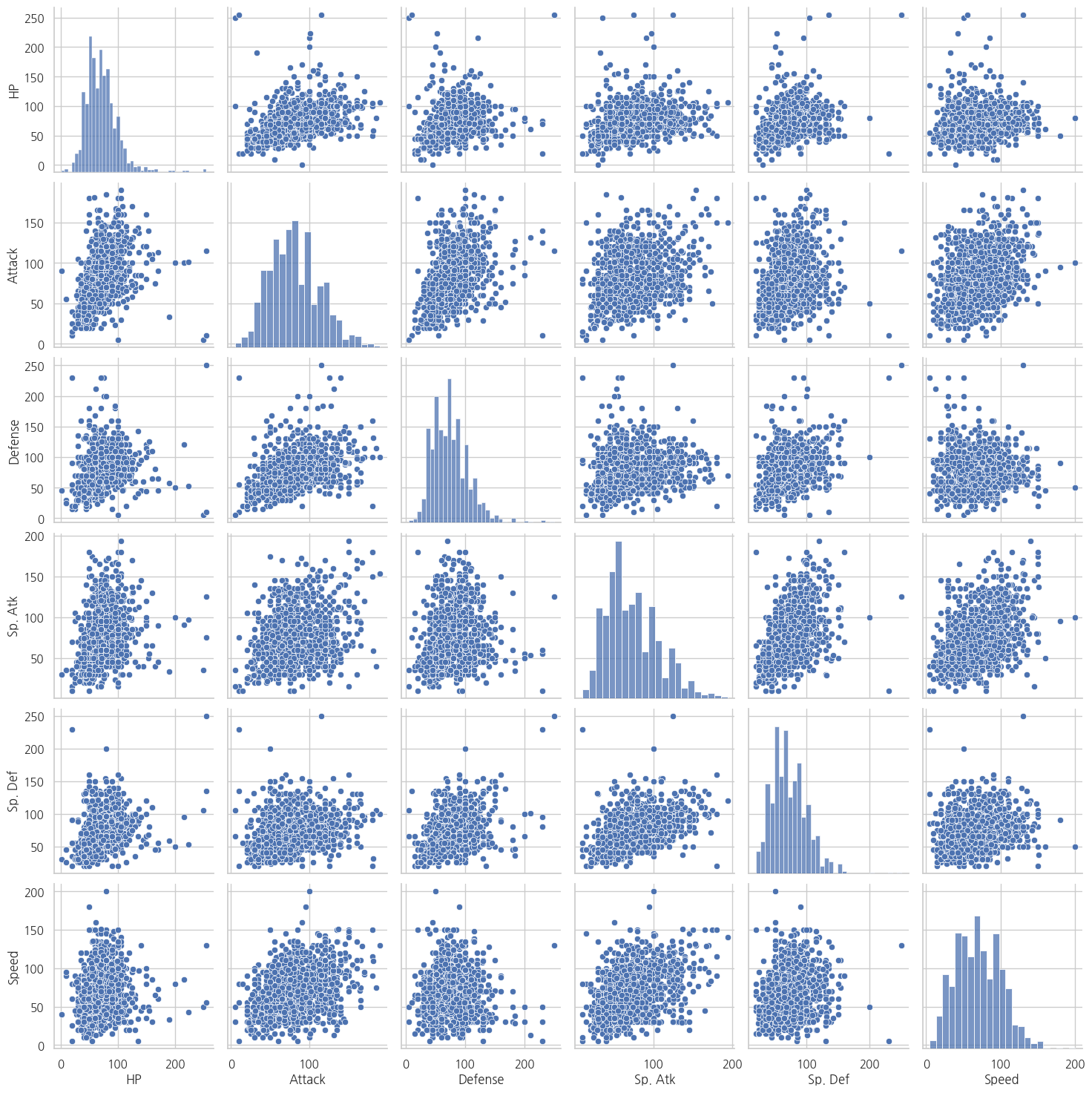

살펴보니 히스토그램은 약간의 positive skewness를 갖는 경향이 있는 것 같고 Scatter Plot도 능력치끼리 양의 상관관계를 일부 보이는 듯하다.

이제 본격적으로 비지도 학습을 시켜보겠다.
포켓몬의 능력치를 특성값으로 사용할 것이고, 데이터 군집화를 하기 전 차원 축소를 해줄 것이다.
(PCA를 사용하려 했으나 PCA보다 t-SNE의 결과가 더 군집화를 실습하기에 적합하여 t-SNE로 차원축소를 진행했다.
t-SNE는 큰 틀로만 이해해서 나중에 PCA와 함께 자세히 공부할 필요가 있겠다.)

from sklearn.manifold import TSNE

tsne = TSNE(n_components=2, learning_rate = 1000, random_state = 928)
result_tsne = tsne.fit_transform(df.iloc[:,4:10])
df[['X', 'Y']] = result_tsne

sns.scatterplot(x = 'X', y = 'Y', data = df)
plt.show()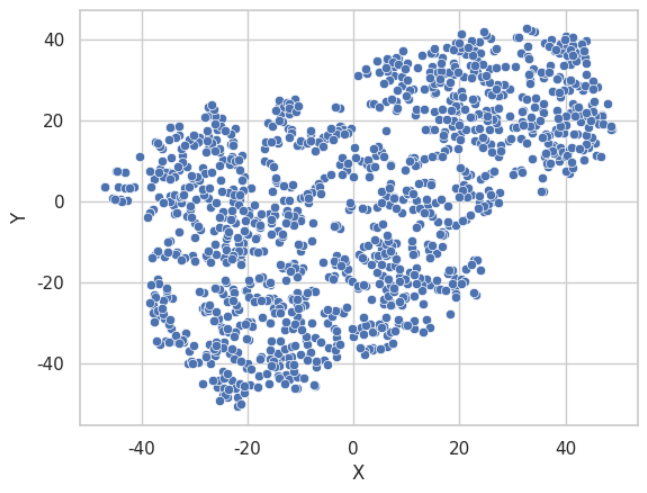

오호,, 뭔가 군집화하고 싶게 생겼다.

우선 K-Means의 K값에 따른 군집화 결과를 보자.

fig, ax = plt.subplots(ncols=3, nrows=2, figsize=(15,8))
fig.subplots_adjust(hspace=0.3)

for i, cl in zip(range(6), range(3,9)):
  kmeans = KMeans(n_clusters=cl, random_state=928, n_init = 'auto')
  label = kmeans.fit_predict(df[['X', 'Y']])
  df['Cluster'] = label
  sns.scatterplot(x = 'X', y = 'Y', hue = 'Cluster', data = df, ax=ax[int(i/3),int(i%3)])
  ax[int(i/3), int(i%3)].set_title(f'Cluster = {cl}')

plt.show()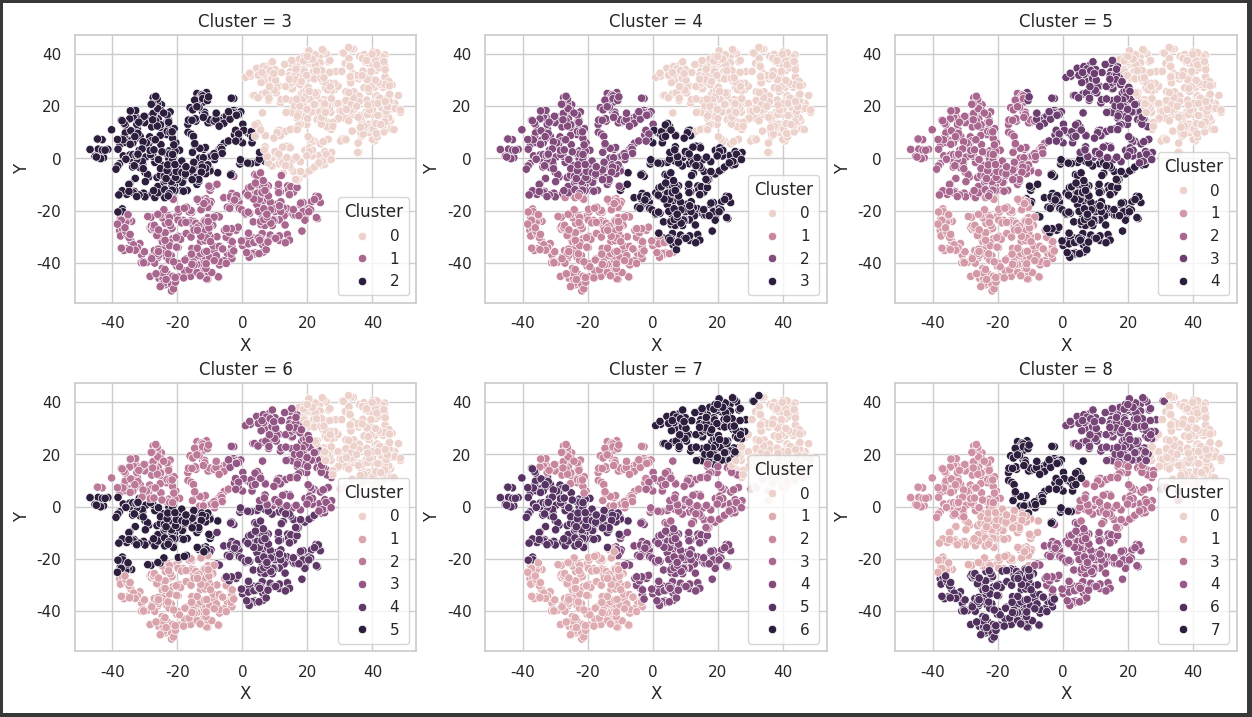

K값이 3 또는 4일 때 데이터를 가장 잘 군집화 한 것 같다. K가 5 이상일 때부터 하나의 군집에 묶여있어야 할 데이터가 억지로 나누어지는 모습을 보인다.

다음으로 DBSCA의 epsilon 값에 따른 군집화 결과를 나타내보자.

import numpy

fig, ax = plt.subplots(ncols=3, nrows=2, figsize=(15,8))
fig.subplots_adjust(hspace=0.3)

for i, ep in zip(range(6), numpy.arange(2,5,0.5)):
  cluster = DBSCAN(eps = ep, min_samples=5)
  label = cluster.fit_predict(df[['X', 'Y']])
  df['Cluster'] = label
  sns.scatterplot(x = 'X', y = 'Y', hue = 'Cluster', data = df, ax=ax[int(i/3),int(i%3)])
  ax[int(i/3), int(i%3)].set_title(f'Eps = {ep}')

plt.show()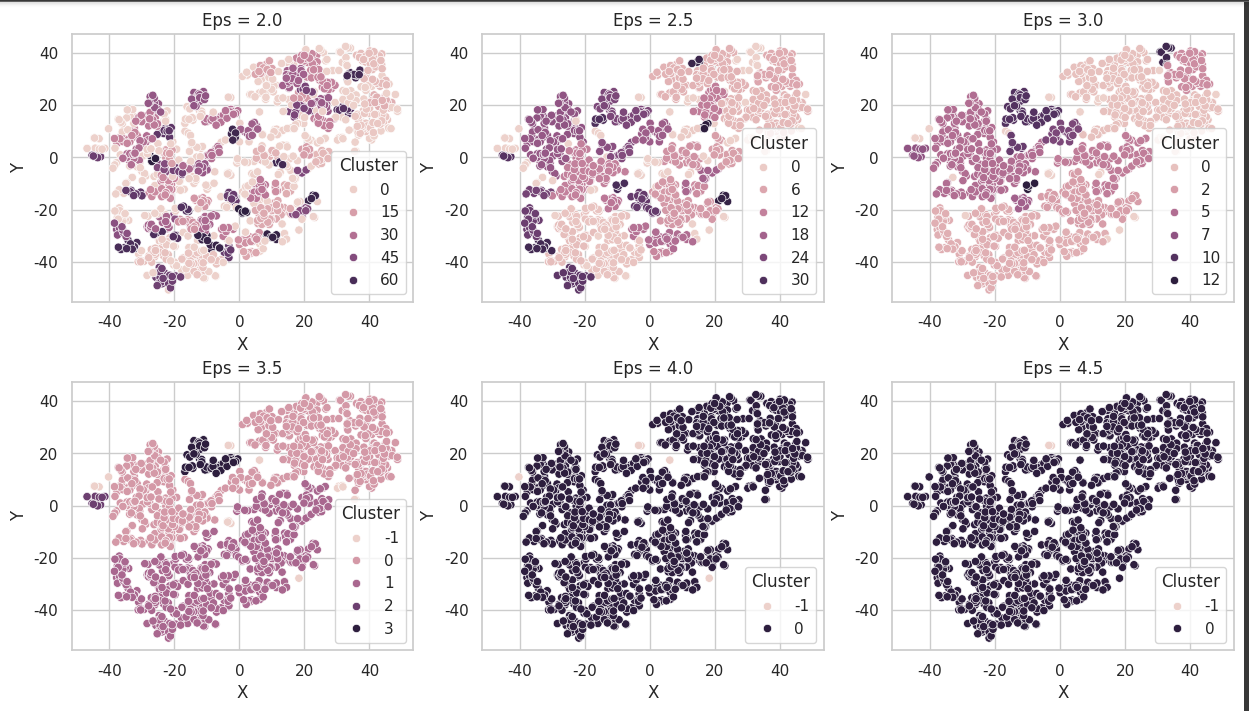

DBSCAN은 epsilon이 3.5일 때 그나마 가장 뭉쳐있는 데이터끼리 군집을 이룬 것 같다.

확실히 비교해보니 K-Means와 DBSCAN의 차이가 명확히 보인다. K-Means는 피자 자르듯 칼로 뚝뚝 잘라낸 느낌이라면 DBSCAN은 가위로 적절히 오려낸 느낌이다. 두 방법의 특성이 잘 드러난 듯 하다.