Dynamic Programming
Divide and Conquer와 Backtracking은 recursion을 이용한 알고리즘이다. 하지만 recursion tree를 그려보면 중복되는 recursion call이 매우 많고 따라서 시간도 오래걸림을 알 수 있다. 대부분의 recursion은 같은 결과값을 알기 위해 같은 동작을 중복해서 한다.
그럼 이렇게 생각할 수 있다. 앞전에 얻은 값을 따로 저장해두고 필요할 때마다 꺼내서 쓰면 안 될까?
이 개념이 바로 Memoization이다. Memoization은 이전에 계산된 값을 기억하고 다시 계산하지 않아도 되기 때문에 프로그래밍에서 최적화 기법으로 사용된다. 주로 배열이나 테이블 등의 자료구조로 구현한다.
Dynamic Programming(이하 DP)는 Memoization을 이용한 알고리즘이다. 작은 하위 문제를 풀고 이 문제들의 답을 이용해 큰 문제를 푸는 방식이다. 이 방식은 recursion과 매우 유사하고 실제로 문제의 해답 또한 recursion으로 찾는다. 하지만 DP는 recursion이 아니라 iteration을 이용한다.
DP는 재귀적으로 해결이 가능한 문제를 반복문을 돌려서 값을 쌓아가는 형식으로 푸는 것이다
How?
DP를 사용하여 문제를 해결하는 일반적인 과정에 대해 알아보자.
1. Formulate the problem recursively ➡️ 문제를 해결하는 recursive 알고리즘 또는 점화식을 찾아낸다.
2. Build Solutions to your recurrence from the bottom up ➡️ base case의 경우부터 답을 차곡차곡 table에 쌓아가는 방식으로 알고리즘을 설계한다
여기서 recursion과 dp의 가장 큰 차이점을 알 수 있다. recursive 알고리즘은 사이즈를 줄여나가면서 계산을 한다. 그러니까 f(n)을 알기 위해선 f(n-1)이나 f(n/2) 등의 값을 알아야 한다. 따라서 top-down 방식이다.
하지만 내가 손으로 직접 문제를 푼다고 생각해보자. 결국 f(1)의 값부터 계산해서 f(n)의 값을 얻어내야 한다. DP는 손으로 푸는 것과 같다. DP는 base case부터 차곡차곡 table에 쌓아가는 bottom-up 방식이다.
참고로 1번 과정에서 문제에 대한 명세를 작성할 때는 how to solve가 아니라 what이 더 중요하다.
2번 과정은 더 세분화할 수 있다. DP를 통해 피보나치 수열 문제를 해결한다고 해보자
- Identify the subproblem
부분문제 개수를 알아야 한다.F(n)=F(n-1)+F(n-2)이므로 부분 문제의 개수는f(0)~f(n)으로 n+1개이다. - Choose a memoization data structure
자료구조를 선택한다. 보통 multidimensional array를 쓴다. 점화식에서 각 recursion마다 사용하는 인자가 하나이므로 1차원 배열을 사용한다. - Identify dependencies
점화식에 다 써있다. 그러니까 f(n)은 f(n-1)과 f(n-2)를 필요로 한다는 관계성을 알고 있으라는 뜻이다. - Find a good evaluation order
좋은 계산 순서를 찾는다. 즉, base case가 1인지 n인지 찾는 것이다. 피보나치 수열은f(0)부터 필요로 하므로 base case가 0이다. - Analyze space and running time
공간 복잡도와 시간복잡도를 계산한다. 자료구조를 쓰기 때문에 공간 복잡도를 구할 수 있다. 피보나치 수열은n사이즈의 1차원 배열을 사용하므로 공간 복잡도가O(n)이다. - Write down the algorithm
지금까지 한 것을 바탕으로 알고리즘을 작성해보자

정말 중요한 것은 올바른 점화식을 찾는 것이다
Dynamic Programming-1
DP를 이용하여 LIS 문제를 풀어보자. 전에 backtracking을 이용하여 LIS를 풀어본 적이 있다. recursive algorithm의 수도 코드와 점화식은 다음과 같다.

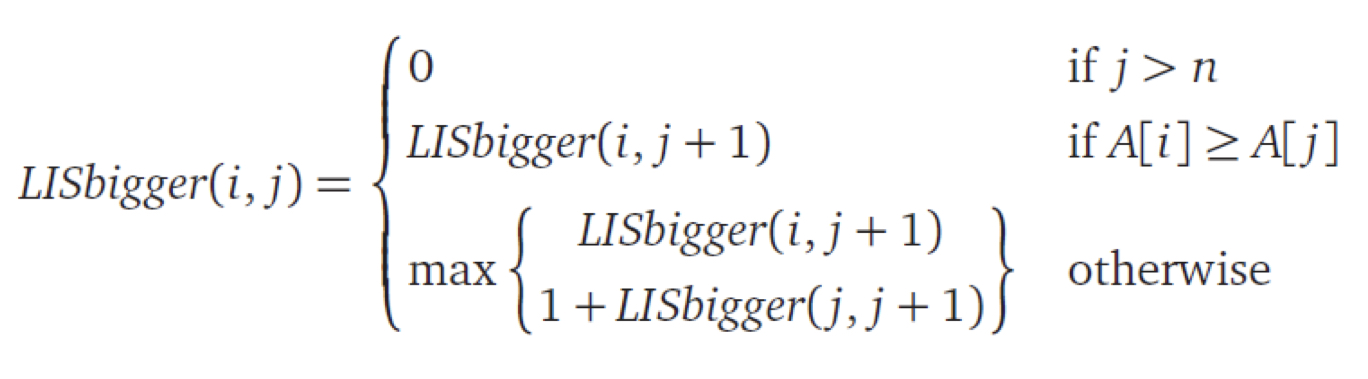
- 항상 함수의 정의를 잘 살피자. LISBigger(i, j)는 length of LIS of A[j...n]이다. 반환 값은 "LIS의 길이"이고 따라서 배열의 LIS를 구하는 답은
LISBigger(0,1)이다
점화식을 통해 알 수 있는 정보들은 다음과 같다
- 함수가 필요로 하는 인자는 2개이다
- base case는
j>n일 때고 그 값이 0이라는 것이다 LISBigger(i,j)의 값을 알기 위해선LISBigger(i,j+1)와LISBigger(j,j+1)의 값을 알아야 한다- 따라서 subproblem의 개수는 LISBigger(i,j) 모두이다. 즉, n^2이다.
✅ 이 때 i의 범위는 0부터 n까지이고 j의 범위는 1부터 n+1까지인데 그 이유는 base case가 j>n이기 때문에 n+1이 필요한 것이다
따라서 우리는
- 2차원 배열(
LISBigger[])을 사용해야 한다 LISBigger[i, j]전에 이미LISBigger[*, j+1]이 채워져 있어야 하므로 배열의 열은n부터1로 채워가야 한다
는 것을 유추해야 한다.
이에 따라 수도 코드를 작성하면 다음과 같다

- 이유가 확실하지는 않지만 i의 반복문이 j-1까지인 것은 다음 단계에서 사용할 값이 LISBigger[j, j+1]가 전부이기 때문이다. 다음 단계의 j는 현재 j-1이므로 여기까지만 배열을 채우면 된다
- 시간 복잡도는
O(n^2), 공간 복잡도도O(n^2)이다.
✅ 기존의 backtracking을 이용한 시간복잡도가O(2^n)이었던 점을 감안하면 엄청난 최적화이다...
배열의 예시를 들어 테이블을 직접 채우고 그 답이 맞는지 확인하자.
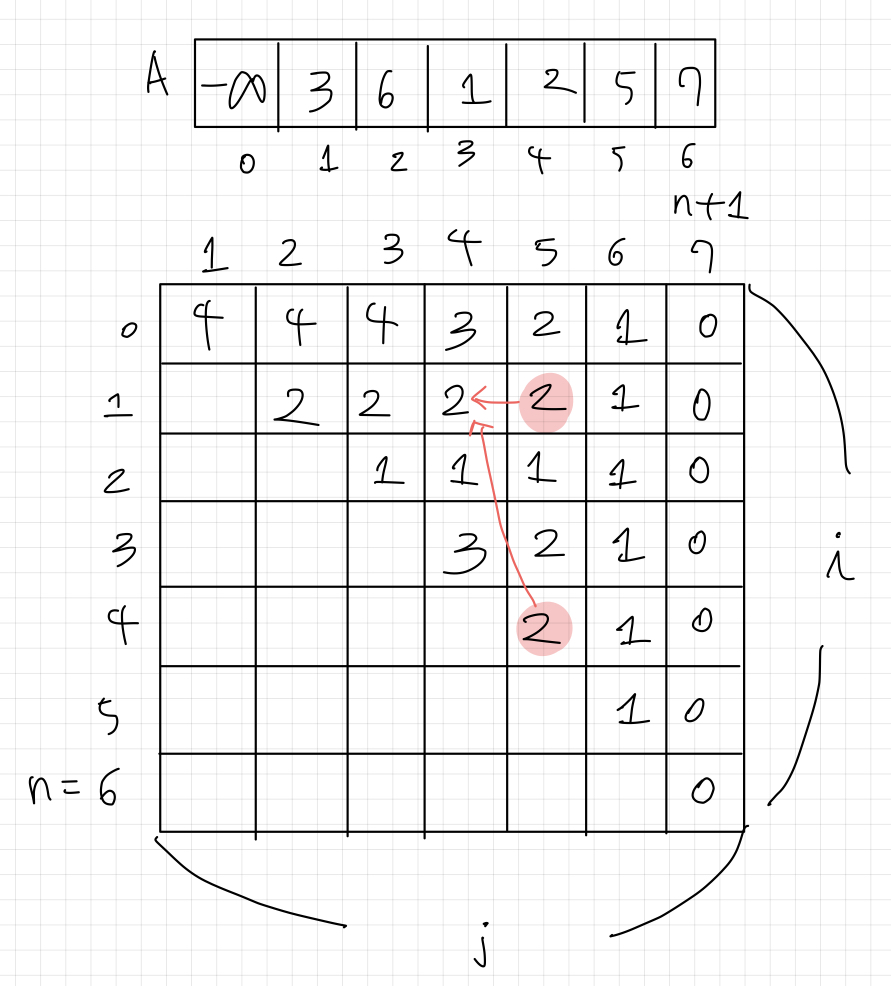
LISBigger[0,1]=4 이므로 알고리즘을 잘 짰음을 알 수 있다.
Dynamic Programming-2
DP를 이용하여 subset sum 문제를 풀어보자. Subset sum은 배열과 양수 T가 주어졌을 때 부분배열의 합으로 T를 만들 수 있는지 없는지를 판단하는 문제이다.
SubsetSum을 backtracking을 이용한 recursive algorithm으로 풀면 다음과 같다.

DP로 이 문제를 풀기 위해서는 약간의 변형이 필요하다. SS(i,t) 를 X[i..n]의 부분배열의 합이 t가 될 수 있는지 아닌지를 반환하는 함수라고 정의하자. 점화식은 다음과 같다.
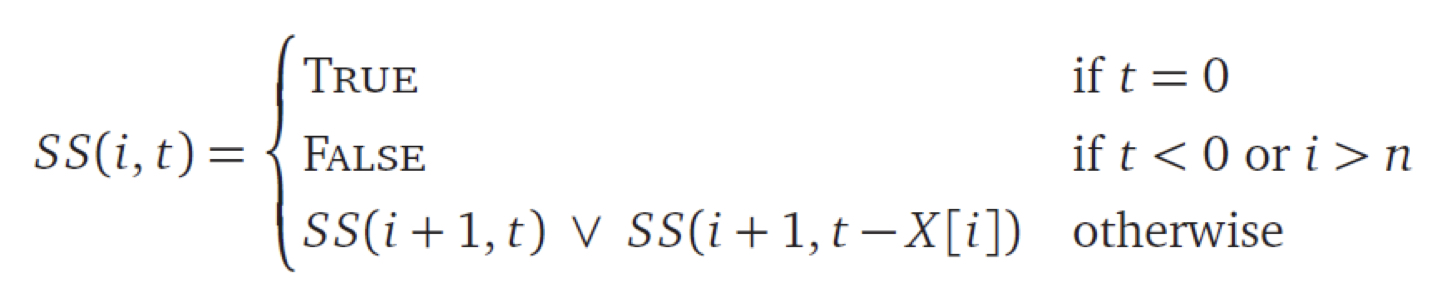
따라서 우리는
- 2차 배열
S[1..n+1, 0..T]를 써서S[i,t]에SS(i,t)를 저장하도록 해야한다 S[i,t]의 계산을 위해S[i+1,*]가 필요하므로 배열의 행은n부터1로 채워가야한다
는 것을 유추해야 한다.
이 때, t가 배열의 열이기 때문에 항상 0이상이 되어야 하므로 부분 문제에 대한 올바른 점화식을 작성한다.

이에 따라 수도 코드를 작성하면 다음과 같다.

t==0이면 무조건 True이다. 어떤 집합이든 공집합이 존재하고, 공집합의 원소의 합은 0이기 때문이다.- 코드에 의하면 어떤 행의 값이 True가 되면 남은 행 중 같은 열의 값들은 모두 True가 된다.
- 시간 복잡도는
O(nT), 공간 복잡도도O(nT)이다
✅ 교수님 말씀으로는 시간을 줄이기 어려운 문제 중 하나라고 하셨다
예시를 들어 테이블을 직접 그려보자. 좌측은 X={8,6,7,5,3,10,9}, T=15일 때, 우측은 X={11,6,5,1,7,13,12}, T=15일 때이다.
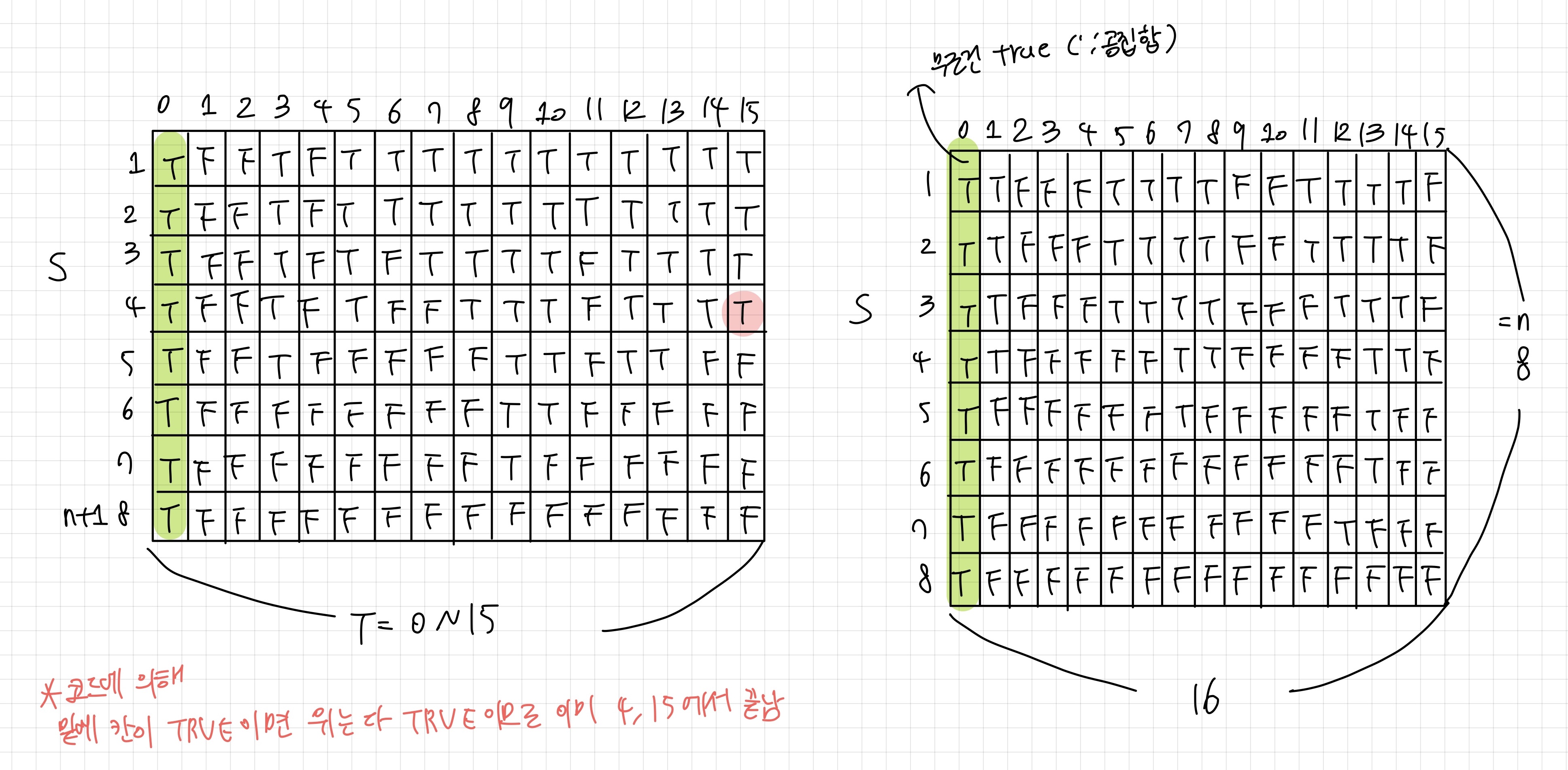
아 정말 어렵다 ... 하지만 내가 중간고사를 생각보다 잘 보지 못했고, 기말고사에서 만회하기 위해선 이렇게 해야할것만 같다... 이게 좋은 방법인지는 모르겠다 🥲
그리고 이어지는 교수님의 명언
귀찮은 것을 귀찮아하면 절대 새로운 것을 배울 수 없다
그래서 저는 열심히 손으로 썼습니다 교수님 😊
