전 포스트에서 Dynamic Programming의 원리를 알고, recursive algorithm으로 풀었던 문제들을 DP를 적용하여 다시 푸는 시간을 가졌다.
DP는 subproblem의 개수가 recursive call보다 훨씬 적은 경우 중복된 계산을 하지 않도록 memoization을 하는 것이다.
결국 DP에서 가장 어렵고 중요한 것은 부분문제 설정과 부분문제에 대한 올바른 점화식이다. 이 결과를 통해 table을 써서 memoization으로 마무리하는 것은 쉽다.
부분문제는 어떻게 계산할 것인가가 아니라 무엇을 계산할 것인가에 초점을 맞춰야 한다. 그리고 부분문제에 대한 정의도 손으로 써두는 것이 좋다.
ex :
F[i] : 피보나치 수열의 i번째 수
S[i,t] :A[i..n] 에서 합이 t와 같은 부분집합이 있는지 없는지
오늘도 몇 가지 예제들을 통해 DP를 적용하는 방법을 알아볼 것이다
Dynamic Programming -3
다음과 같은 경우에 (0,0)에서 (m,n)으로 가는 최단경로는 총 몇가지 일까?
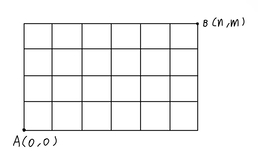
임의의 교차점 (i,j)까지 가는 방법을 구하기 위해 보통 우리는 왼쪽과 아래쪽까지 오기 위한 각각의 최단 경로를 더한다.
P(i,j)를 (0,0)에서 (i,j)까지 가는 최단경로 개수라고 정의할 때 점화식을 구하면 다음과 같다.
P(i,j)=P(i-1,j)+P(i,j-1)- 함수가 인자를 2개를 받으므로 2차원 배열을 사용하면 좋을 것이다. 행과 열의 범위는 0~n, 0~m이다.
i==0또는j==0일때 갈 수 있는 경로가 1개 뿐이므로 base case는i==0또는j==0일 때 1로 생각할 수 있다.
이를 통해 수도 코드를 작성하면 시간 복잡도와 공간 복잡도 모두 O(mn)이 나온다.
Dynamic Programming -4
String Matching이란 두개의 문자열이 주어졌을 때, A와 B의 문자열을 비교하거나 동일한 부분 문자열이 존재하는지 유무 등을 판단하는 문제이다.
DP로 풀어볼 첫 번째 String Matching 문제는 Longest Common Subsequence이다. (문자열은 배열로 주어진다)
예를 들어 A={A,B,C,D,E,F,G,H,I,J,K,L,M}이고 B={A,L,G,O,R,I,T,H,M} 일 때 Common Subsequence는 A, L, G, AL, AG, AIM, ... , AGHM, AGIM 등이 있고 그 중 Longest Common Subsequence는 AGHM, AGIM 이다.
일단 backtracking을 이용한 recursive algorithm을 찾아보자.
L(i,j)를 A[1..i]와 B[1..j] 사이의 LCS의 길이로 정의하자- 우리가 얻어야할 답은
L(m,n)이고 나머지L(i,j)의 값들을 구하는 것이 부분문제이다. (i: 0~m-1, j: 0~n-1)
A[i]와 B[j]가 각 배열의 가장 마지막 원소이므로 둘을 비교하여 나머지를 줄여 나가는 방식을 생각하면 다음과 같은 경우들이 나온다.
-
(A[i]==B[j]) 둘을 매칭시켜서
A[i]와B[j]를 다 지우고 나머지(앞)의 경우에 대해 진행 :L(i-1,j-1)+1➡️ 같으면 포함 -
a. (A[i]==B[j])
A[i]가B[j]이전의 B의 원소와 동일한 경우가 있을 수도 있고, 그 때 매칭시켜 얻은 Common Subsequence의 길이가 더 길 수도 있으므로 일단A[i]와B[j]를 매칭시키지 않는다. 따라서,B[j]가 필요없어지므로B[j]를 지우고 나머지에 대한 계산을 하는 경우 ➡️ 같아도 미포함
b. (A[i]!=B[j]) B[j]가 A의 문자 중 아무것과도 매칭되지 않을 수 있으므로 B[j]를 지우고 나머지에 대해 진행
:L(i,j-1) -
2번의 반대의 경우
L(i-1,j)
이런식으로 i에서 i-1, j에서 j-1로 줄여나가는 것이 나머지에 대한 부분문제로 줄여가는 방법이다
base case: A나 B중 하나라도 empty string일 경우, 그 값은 그냥 0 이므로 i==0 또는 j==0일때 0
위 1~3과 base case에 따라 점화식을 작성하면 다음과 같다.
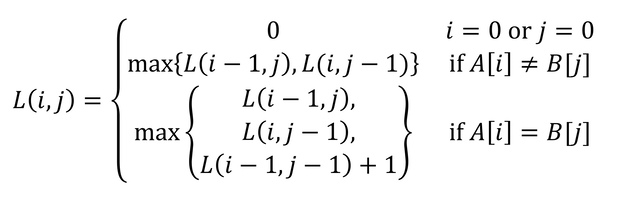
- 함수가 인자를 2개 받으므로 2차원 배열을 사용한다.
L(i,j)를 알기 위해선L(i-1,j)또는L(i,j-1)을 알아야 하므로L[]의 행과 열 모두 증가하는 순서로 반복문을 돌린다
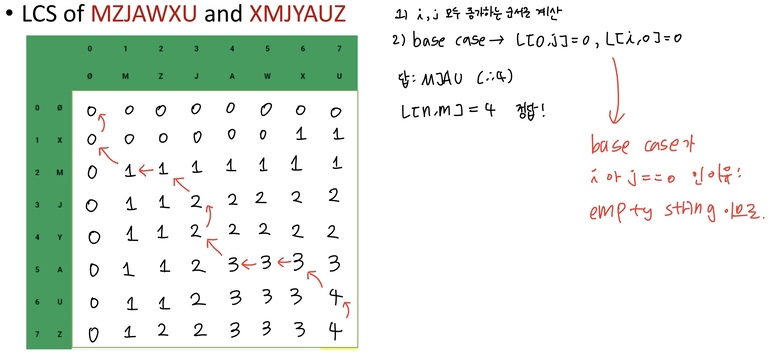
A={X, M, J, Y, A, U, Z}이고 B={M, Z, J, A, W, X, U}일 때를 예로 들어 LCS를 구하는 table을 직접 그려보면 다음과 같다.
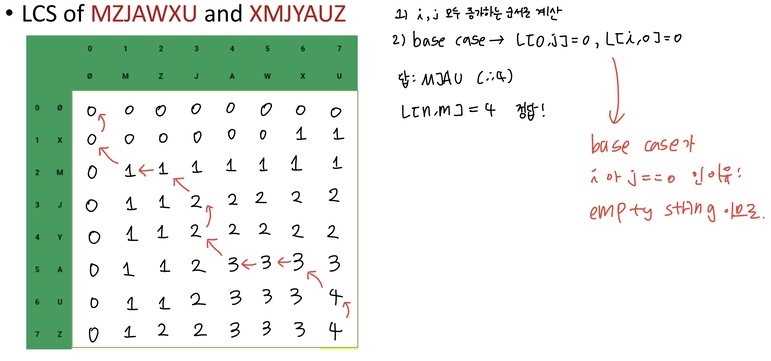
마찬가지로 시간 복잡도와 공간복잡도 모두 O(nm)이다.
Dynamic Programming -5
DP로 풀어볼 두 번째 String Matching 문제는 Edit distance이다.
Edit distance는 문자열 A를 B로 변환하기 위해 필요한 최소 횟수의 편집 연산이다.
예를 들어, A= FOOD 이고 B= MONEY일 때 필요한 편집 과정과 최소 횟수는
FOOD (대체) ➡️ MOOD (대체) ➡️ MON^D (삽입) ➡️ MONED (대체) ➡️ MONEY 로 총 4번이다.
bactracking을 이용한 recursive algorithm을 고안해보자.
첫 번째로, 계산할 값이 무엇인지 설정하고 정의해야한다.
Edit (i,j)를A[1..i]와B[1..j]사이의 edit distance로 정의한다.- 우리가 얻어야 할 결과는
Edit(m,n)이다. - 따라서 나머지 i,j 에 대한
Edit(i,j)의 값들을 구하는 것이 부분문제이다 (i: 0~m-1, j: 0~n-1).
두 번째로, 어떻게 계산할지 생각한다.
배열의 마지막 값, 그러니까 A[i]와 B[j]를 비교하여 나머지를 줄여나가는 방식을 떠올릴 수 있다.
마지막 열에 대한 4가지 경우의 수가 있다.
- Insertion ➡️ 마지막 열의 위(
A)가 비어있다 - Deletion ➡️ 마지막 열의 아래(
B)가 비어있다 - Substitution ➡️ 모두 채워져있으나 서로 다름
- Match ➡️ 모두 채워져있고 서로 같음
각 경우에 대해 Edit(i,j) 에 대한 관계식을 작성하면 그 결과가 점화식이다.
네 개의 경우 중 무엇이 가장 작을지 모르므로 backtracking을 사용하는 것이다. 사용하는 이유를 항상 까먹지 않아야 한다.
세 번째로, 관계식을 작성하고 점화식을 얻어낸다.
다음은 insertion의 경우이다.
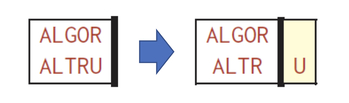
이 경우 나머지 문제에 대해 A의 개수는 똑같이 i이고 B의 개수는 하나 줄어든 j-1 이다. 실제 배열에는 빈공간이 없지만 어떤 경우에 최소 횟수가 될지 모르므로 빈 공간으로 가정한 것이기 때문이다. 따라서 관계식은 Edit(i,j)= Edit(i,j-1)+1 이다.
같은 사고방식으로 나머지에 대해 관계식을 작성하면
Deletion ➡️ Edit(i,j)= Edit(i-1,j)+1
Substitution ➡️ Edit(i,j)= Edit(i-1,j-1)+1
Match ➡️ Edit(i,j)= Edit(i-1,j-1) (마지막 글자가 같으면 편집 연산이 필요 없음)
의 결과를 얻을 수 있다.
얻은 결과에 따라 점화식을 작성하면 다음과 같다.
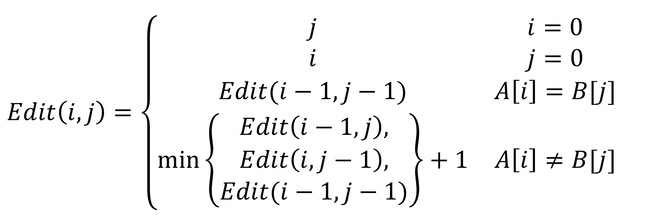
- 함수가 인자를 2개 사용하므로 2차원 배열을 사용한다.
- Edit(i,j)를 계산하기 전에 Edit(i-1,j-1)이 이미 계산되어있어야 하므로 i와 j모두 증가하는 방향으로 계산해야한다.
- empty string일 경우 insertion을 i 또는 j번 진행하므로 base case를 설정할 수 있다.
아래는 내가 작성한 수도 코드이다 😊