알고리즘

백준 단계별 풀어보기 기본 수학2의 1929번을 풀면서 내가 모르는 소수 구하기 알고리즘을 알게 되었다 뿐만 아니라 굳이 n까지 확인할 필요가 없다는 것을 알게 되었다지금까지 나는 n이 주어지면 2부터 n까지 나눠서 소수인지 합성수인지 판별했다하지만 n이 아니라 n의

내가 이해한 것을 나중에 까먹고 헤맬까봐 내 언어로 정리한 글참고한 사이트 선택정렬, 버블정렬, 삽입정렬의 시간 복잡도는 모두 O(n^2) 이다 데이터가 10만개만 되어도 100만의 시간복잡도를 가지는 것이다 ... 최악 ㅜㅡㅜ 반면 퀵 정렬의 시간 복잡도는 O(n\

백준 2751번을 풀고 시간 초과로 애를 먹던 중 counting 정렬을 접하게 되었다st_lab님의 글을 보고 내 언어로 정리한 것이다퀵 정렬, 합병 정렬 등은 O(nlogn)의 시간 복잡도를 갖는다. 특히 퀵 정렬은 최악의 경우 O(n^2)의 시간복잡도를 갖는다 (

내가 하는 힙은 메모리밖에 없는디 개요

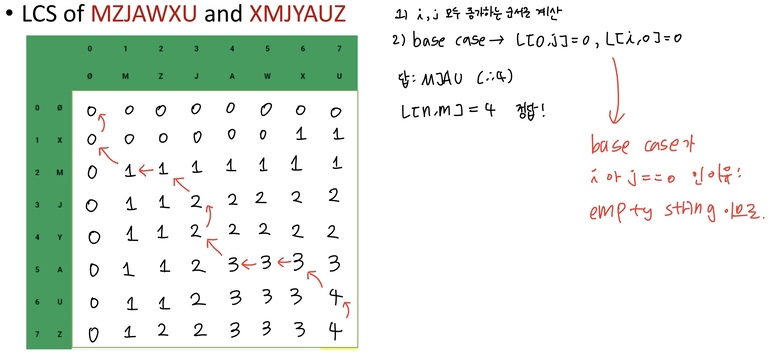
전 포스트에서 Dynamic Programming의 원리를 알고, recursive algorithm으로 풀었던 문제들을 DP를 적용하여 다시 푸는 시간을 가졌다. DP는 subproblem의 개수가 recursive call보다 훨씬 적은 경우 중복된 계산을 하지

Dynamic Programming Divide and Conquer와 Backtracking은 recursion을 이용한 알고리즘이다. 하지만 recursion tree를 그려보면 중복되는 recursion call이 매우 많고 따라서 시간도 오래걸림을 알 수 있다.