[기초 통계] 모집단과 표본분포

모집단 (population)과 표본(sample)

이미지 출처 : Population vs Sample

Population
Mean: μ = (ΣX)
Standard Deviation: σ = √[(Σ(X-μ)²) / N]

Sample
Mean: x̄ = (Σx) / n
Standard Deviation: s = √[(Σ(x-x̄)²) / (n-1)]

표본추출 (sampling)

모집단으로부터 표본을 추출하는 것을 sampling 이라고 하며, 표본으로부터 그 특성을 찾아내고 모집단의 특성을 추론하고자함

• 복원 추출
• 비복원 추출
• Random Sampling

복원 추출 (sampling with replacement)

모집단에서 데이터를 추출 할 때 하나를 추출하고 다시 넣고 추출하는 방법으로 동일한 표본이 추출 될 수 있음

비복원 추출 (sampling without replacement)

모집단에서 데이터를 추출 할 때 하나를 추출하고 다시 넣지 않고 추출하는 방법

Random Sampling

모집단에서 데이터를 추출할 때 주의할 점은 편향되지 않아야 함, 각 개체가 모두 동일한 확률로 추출하는 방법

---

불균형 데이터 문제

데이터가 불균형 데이터 일 경우 문제가 생김

• Sampling 기법을 통해해결
• 모델을 통한 성능 개선

Sampling 기법

관심의 대상이 아주 낮은 비율인 경우

✅Over Sampling

타겟이 적은 class의 수를 많은 class의 비율만큼 증가 시킴 (일정 비율로 복원추출하는 개념)

문제점 : 과도적합

✅Under Sampling

타겟 데이터의 많은 class의 수를 적은 class의 비율만큼 감소 시킴

문제점 : 임의로 뽑은 데이터가 편향될 수 있고, 모형의 성능이 떨어질 수 있음

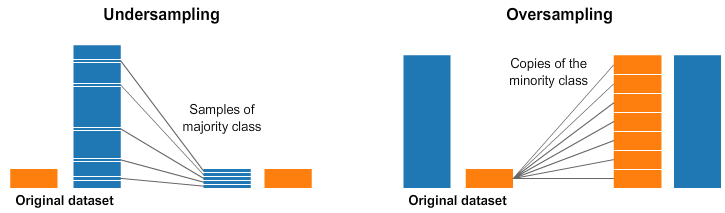
이미지 출처 : Resampling strategies for imbalanced datasets

---

표본분포

통계량(Statistic): 표본에 기초하여 계산되는 수치 함수

표본분포(Sampling distribution)

통계량을 이루는 분포를 표본분포라고 한다.

Sample
Mean: x̄ = (Σx) / n
Standard Deviation: s = √[(Σ(x-x̄)²) / (n-1)]

표본평균의 기대값

$E(\overline{X})={\displaystyle \frac{1}{n}}[E(X_1)+E(X_2)+\cdots +E(X_n)]$

$E(\overline{X})={\displaystyle \frac{1}{n}}[\mu +\mu +\cdots +\mu ]$

$E(\overline{X})={\displaystyle \frac{1}{n}}[n\mu ]=\mu$

표본평균의 분산

$Var(\overline{X})=Var({\displaystyle \frac{1}{n}}{X}_1+{\displaystyle \frac{1}{n}}{X}_2+\cdots +{\displaystyle \frac{1}{n}}{X}_n)$

$Var(\overline{X})={\displaystyle \frac{1}{n^2}}Var(X_1)+{\displaystyle \frac{1}{n^2}}Var(X_2)+\cdots +{\displaystyle \frac{1}{n^2}}Var(X_n)$

$Var(\overline{X})={\displaystyle \frac{1}{n^2}}[n{\sigma }^2]={\displaystyle \frac{{\sigma }^2}{n}}$

참고 : Mean and Variance of Sample Mean

중심극한 정리(central limit theorem)

평균이 μ 이고 σ² 인 임의의 모집단에서 랜덤 표본 X1,X1,X3 … ,Xn 을 추출할 때 표본의 크기 n이 충분히(n>=30) 크면, 표본평균 x̄ 는 근사적으로 정규분포 N(μ, σ²/n)을 따른다.

$\overline{X}\sim N(\mu ,{\displaystyle \frac{{\sigma }^2}{n}})$

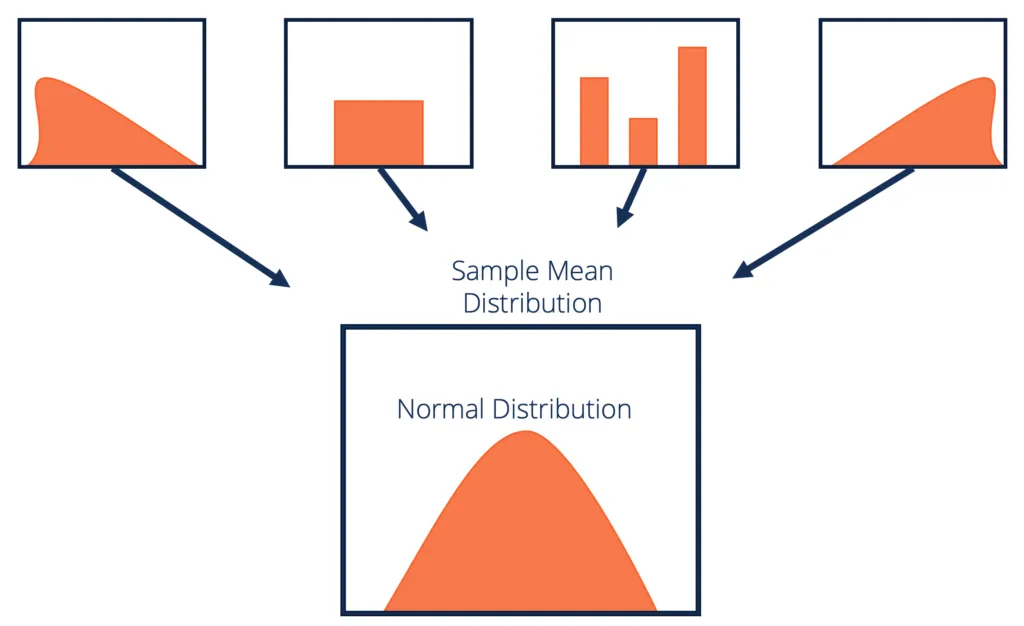
이미지 출처 : Central Limit Theorem

📑 예제

모집단의 분포가 X ~ N (30, 5²) 일때, 이 모집단으로 부터 크기가 30 인 확률 표본의 평균 x̄가 32 이하일 확률은?

평균 : 30
분산 : 5²/30

P(x̄<=32) = P(x̄-μ/5√30 <= 32-30//5√30 )
        

---

카이제곱 분포(Chi-square distribution)

양의 정수 k에 대해 k개의 독립적이고 표준정규분포를 따르는 확률변수 X₁X₂... Xₖ 를 정의하면 자유도 k의 카이제곱 분포는 확률변수

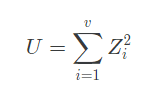
의 분포이다

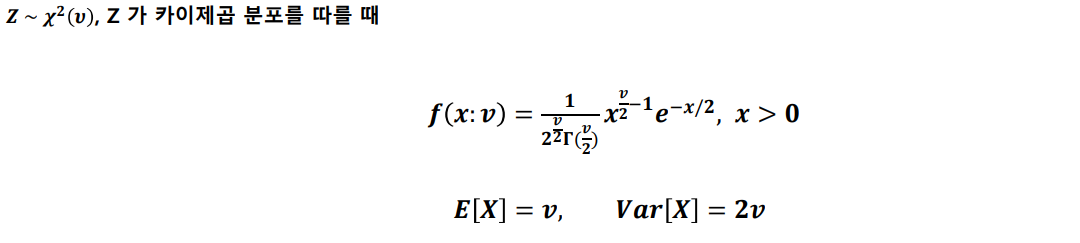
자유도 : 몇 개의 표준정규분포 변수를 더한 것인가?

이미지 출처 : https://www.scribbr.com/statistics/chi-square-distributions/

카이제곱분포는 오차 혹은 편차를 분석할 때 쓰이며 범주형 자료분석에서 활용한다.

자유도 (degree of freedom)

표본수 - 제약조건의 수 또는 표본수-추정 해야하는 모수의 수를 의미하며 일반적으로 n-1을 사용함

예를들어, 표본의 크기가 5이고, 표본 평균이 3로 정해졌다면, 숫자4개는 자유롭게 정할 수 있으나 마지막 하나의 숫자는 나머지 네 개의 숫자에 의해 결정

자유도 v의 크기에 따라 모양이 달라짐 자유도가 커질수록 분포가 좌우 대칭 형태로 됨
자유도가 커지면서 표본정규 분포에 근사하며, (v>=30) 이면, 확률을 근사적으로 정규본포를 구할수 있음

---

T분포

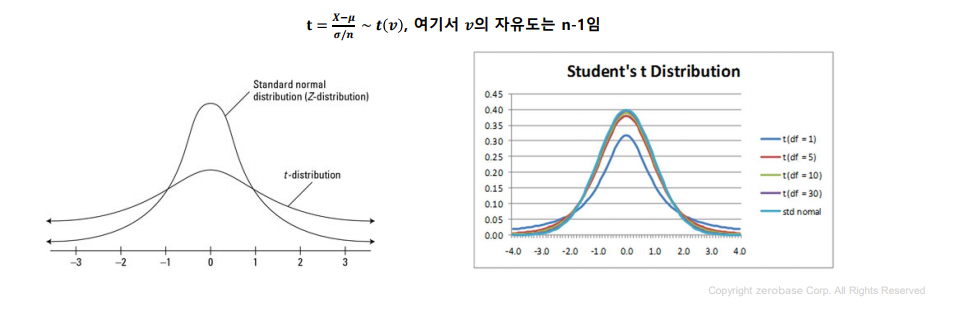
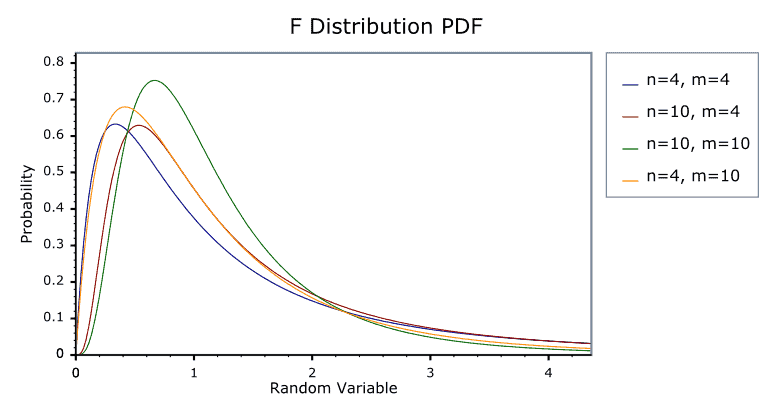
F분포

서로 독립인 두 정규모집단의 분산 또는 표준편차들의 비율에 대한 통계적 추론, 분산분석 등에 활용됨

이미지 출처 : sixsigmastudyguide.com