충남대학교 컴퓨터융합학부의 김동일 교수님의 기계학습을 수강한 후 정리한 글입니다.

• Bayesian Classification
• Linear Regression

지난번 Bayesian에 이어 오늘은 Regression에 대해 알아보려고 한다.

Regression

Output 이 어떠한 클래스로 분류할 수 없고 연속적인 형태를 띄고 있을 때 Input 과 Output 의 관계를 Regression 이라고 한다. 이들 사이의 관계가 선형적인 경우 Linear Regression , 그렇지 못한 경우 Nonlinear Regression 이라고 한다.

특징

• 예측 가능한 모델
• 지도 학습
• Output이 연속적(Continous)
• Input과 Output 사이의 관계

Linear Regression

종류

• Linear Regression (Univariate)
• Multivariate Linear Regression (Multivariate)
• Lasso and Ridge Linear Regression (Regularized)
• Neural Network Regression
• Support Vector Regression
• Decision Tree Regression

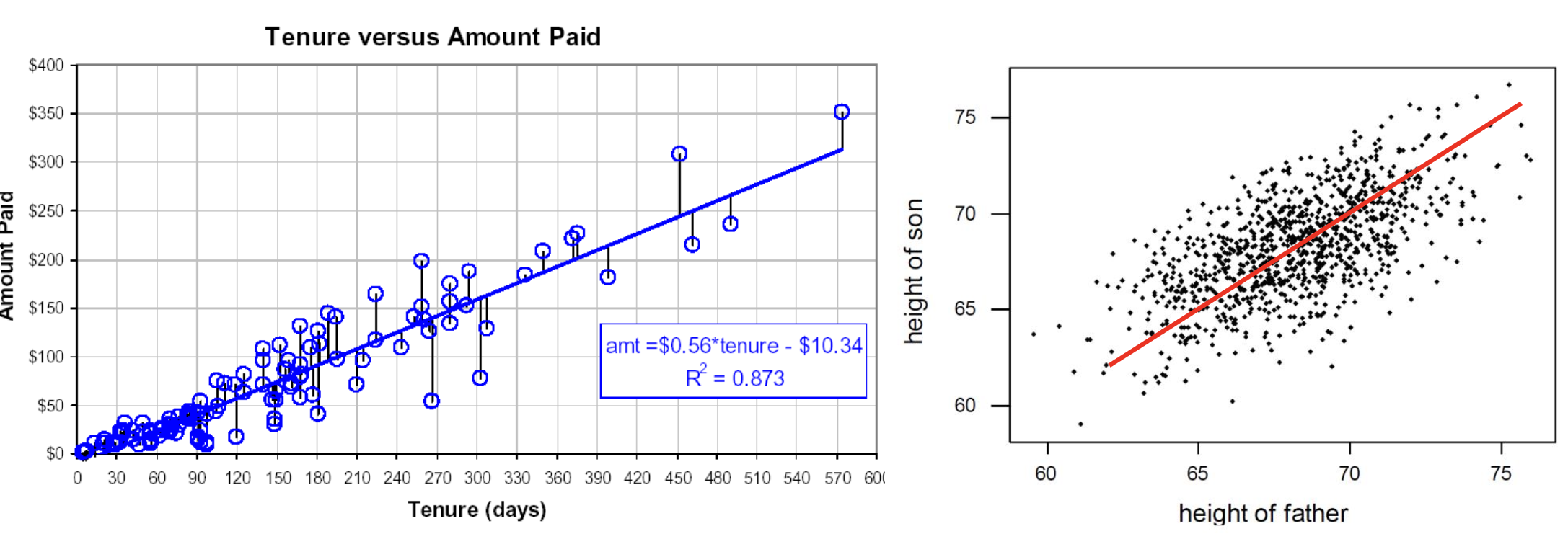
주어진 데이터를 가장 잘 설명할 수 있는 선형방정식을 찾는 것이 우리의 목표이다.

For Input

Bayesian Classification 에서와 마찬가지로 Input 의 개수에 따라서 Univariate , Multivariate 가 나뉜다.

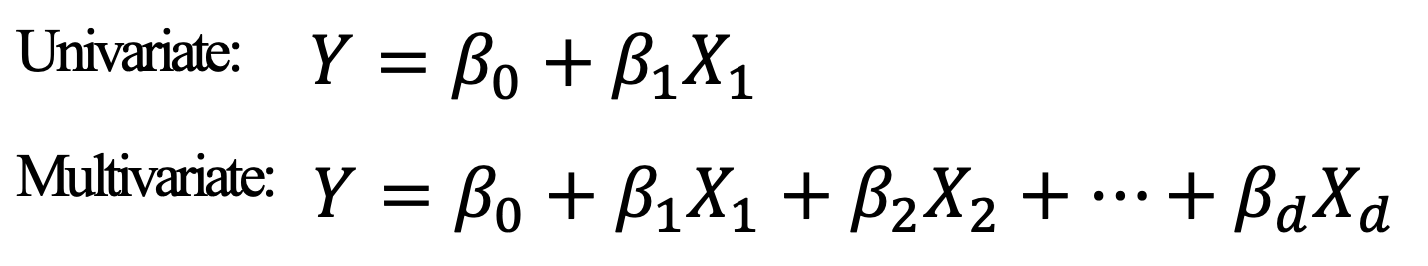
우리가 접하는 Linear Regression 문제는 대부분 Multivariate 이다.

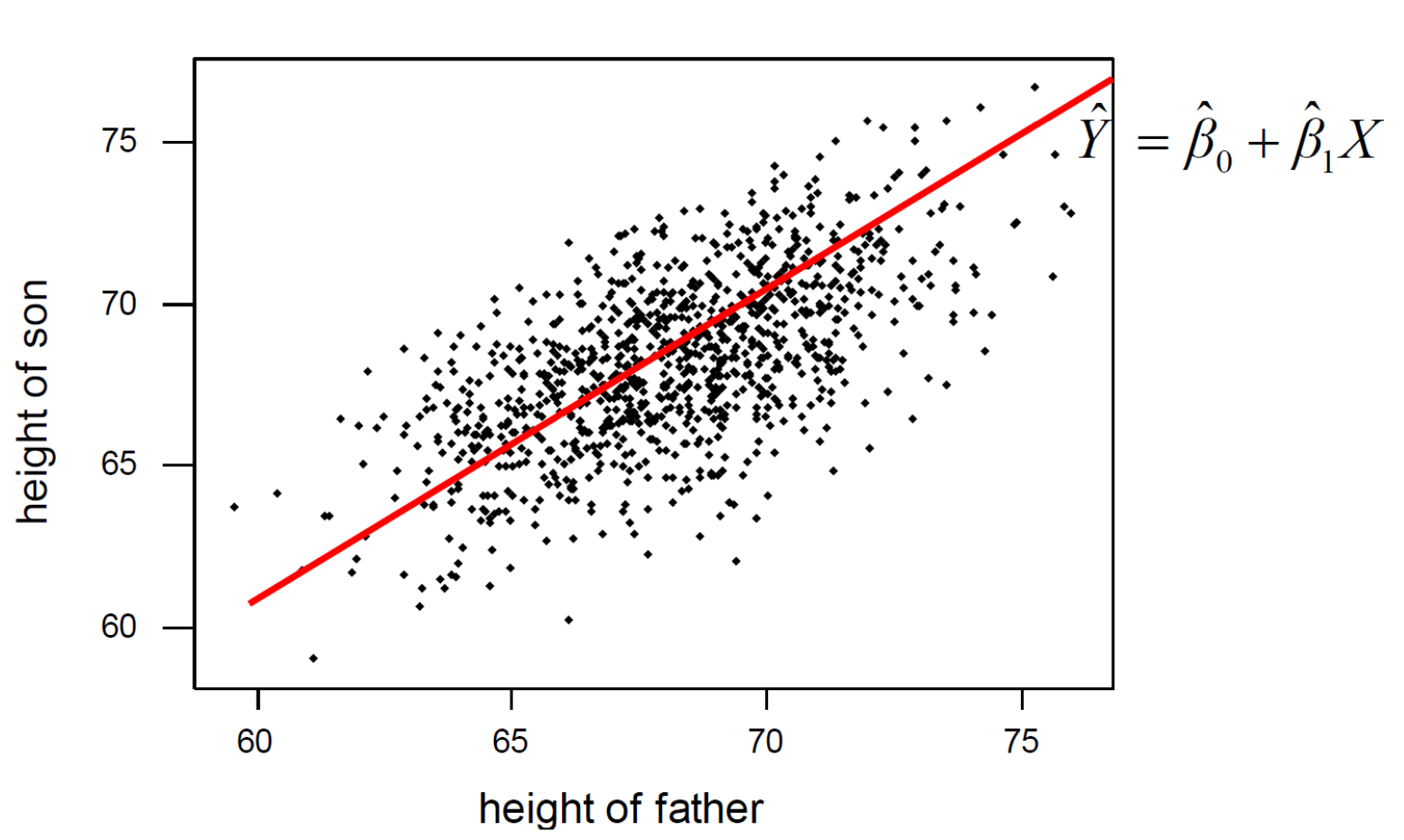
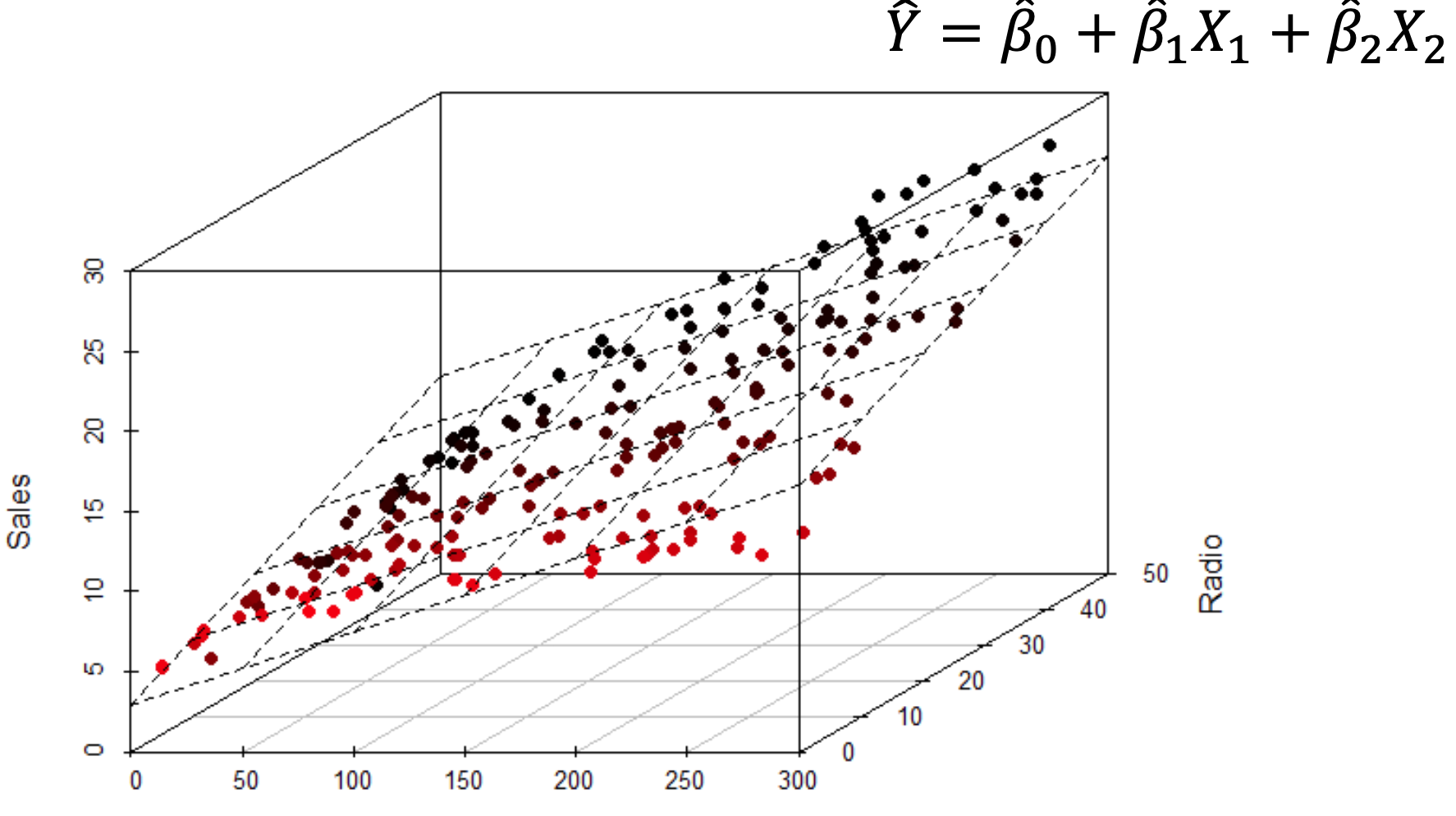
Univariate 은 2차원으로 표현이 가능하지만Multivariate 는 최소 3차원 이상이다.

적용

우리의 데이터를 가장 잘 설명할 수 있는 선형방정식을 찾아야하는데 이를 어떻게 찾을 수 있을까? 잘 설명할 수 있다는 것은 그만큼 데이터와의 오차가 적다는 것을 의미한다. 따라서 오차가 가장 적은 선형방정식을 찾으면 된다.

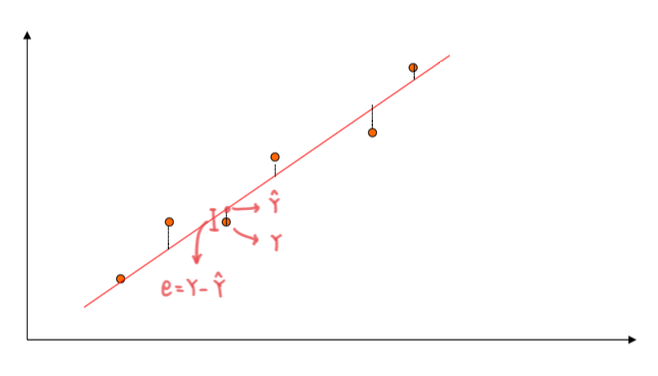
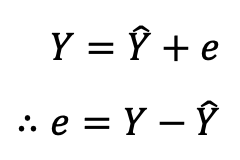
오차는 실제 값 - 예측 값 으로 나타낼 수 있다. 하지만 위의 식에서 예측 값이 실제 값보다 더 크게되면 오차가 음수가 된다. 이를 해결하기 위해 오차에 제곱을 취해주는데 이것이 바로 RSS(Residual Sum of Square) 이다.

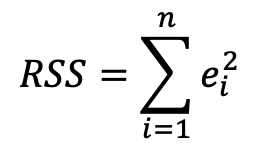
이 RSS 를 작을수록 오차가 작다는 것을 의미하고 이는 결국 우리가 예측한 선형방정식이 실제 값을 잘 설명한다는 것을 뜻한다.

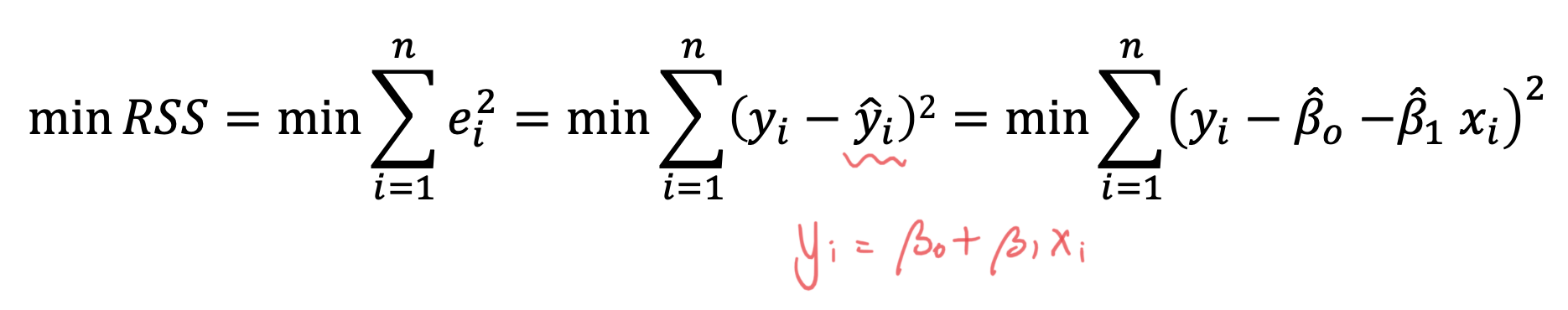
RSS 를 이와 같이 표현할 수 있고 RSS 가 최소가 되는 값을 찾기 위해서 역시 미분을 진행한다.

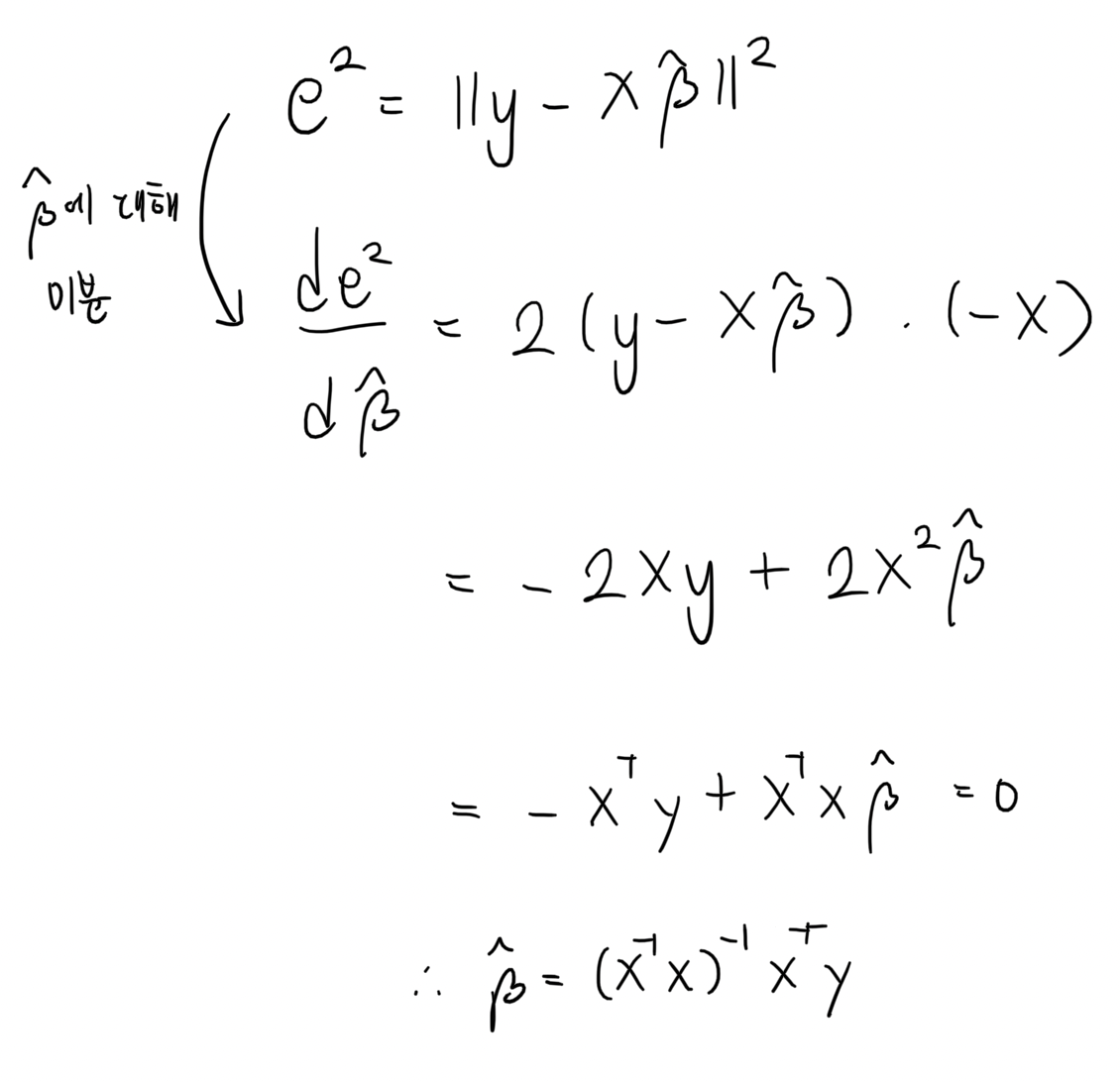
그 결과 선형방정식의 계수들의 값에 대한 식을 구할 수 있다.

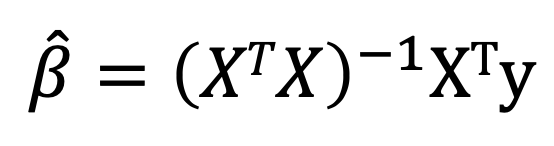
성능 측정

그렇다면 우리가 구현한 모델을 성능을 어떻게 측정하고 평가할 수 있을까? 성능을 측정하기 위해선 기준이 필요하다. 이 때 오차를 사용한다. 위에서 말한 것처럼 모델과 실제 값의 오차가 작을수록 잘 설명한다고 볼 수 있다. 따라서 오차가 성능 측정 기준이 된다.

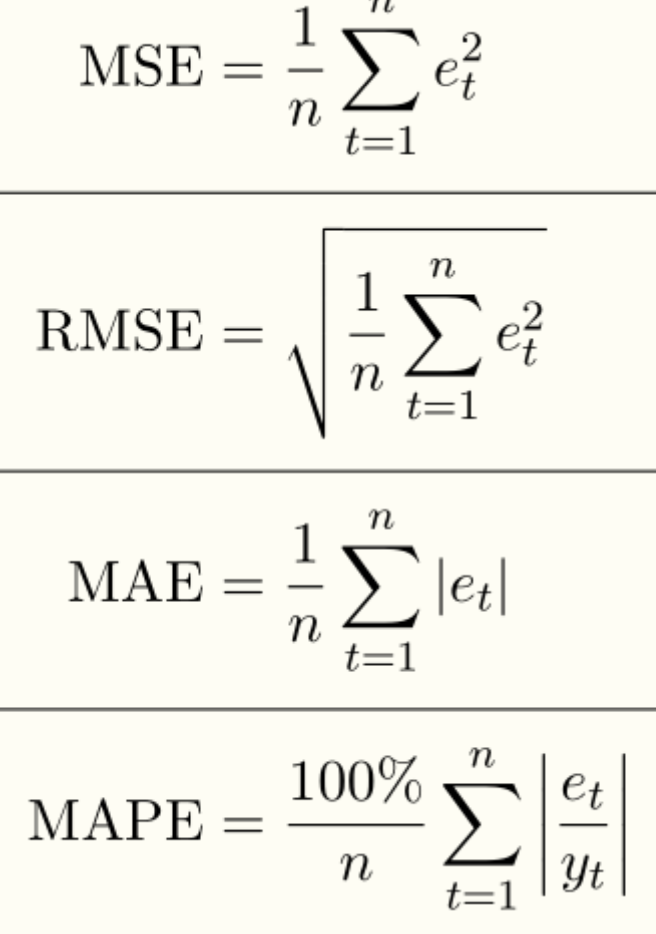
• MSE (Mean Square Error)
  가장 기본적인 식이다. 부호의 영향을 없애기 위해 제곱을 취했고, 미분이 가능하다. 하지만 오차 자체를 가지고 평가하는 것이 아닌, 제곱을 취했기 때문에 실제로 오차 자체가 얼마나 차이가 나는지 모른다는 단점이 있다.

• RMSE (Root Mean Sqaure Error)
  MSE 에 Root 를 씌어줬다. MSE 에서는 제곱을 취했기 때문에 오차의 Scale 이 오차 자체의 값보다 커지는데 이를 방지하기 위해 Root 를 씌어줬다. 하지만 Extreme Point 에 의해서 RMSE 가 커질 수 있다는 단점이 있다. 가령 오차가 1, 10, 100 이 나왔고 이들의 RMSE 를 계산하면 루트111 = 11 이라는 결과가 나온다. 100에 의해서 RMSE 가 커지는 것을 볼 수 있다.

• MAE (Mean Absolute Error)
  MSE 와 RMSE 의 문제점이였던 Extreme Point 에 의해 값이 커지는 것을 방지하기 위해 제곱을 취하지 않고 절대값을 취한다. Extreme Point 의 영향력은 줄어들었지만 제곱의 형태가 아니기에 미분 값이 0인 곳을 찾기가 어려워졌다.

• MAPE (Mean Absolute Percentage Error)
  MAE 가 변수의 Scale 의 영향을 받는 것을 해결하기 위해 비율로 계산했다.

R2

결정계수라고 불리는 R2 은 선형회귀의 성능 측정 방법 중에 하나이다. 우리는 우리가 구현한 선형회귀 모델이 실제 값을 얼마나 잘 설명하는지를 알고 싶다.

• SST(Sum of Squares Total) : 편차의 제곱

• SSR(Regression of Sum of Squares) : 예측 값 - 실제 값 의 제곱

• SST(Sum of Squares Error) : 실제 값 - 예측 값 의 제곱

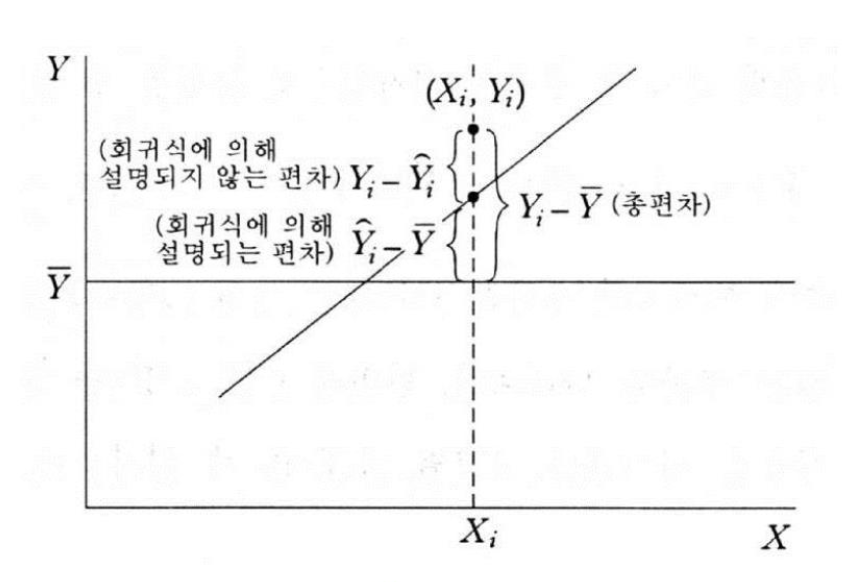
위 그림을 보면 좀더 이해가 잘 될 것이다.

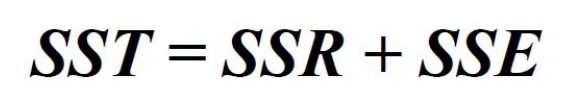
이러한 식을 갖는다. SSR 은 우리가 구현한 모델을 통해서 설명할 수 있는 오차이고 SSE 는 설명할 수 없는 오차이다. 따라서 SSE 를 최소화하는 것이 우리의 궁극적인 목표.

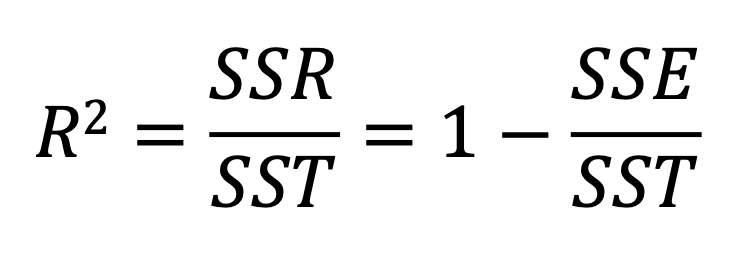
편차에서의 SSE, 즉 우리의 모델이 설명할 수 없는 오차가 작을수록 더 적합한 모델이라는 뜻이다.

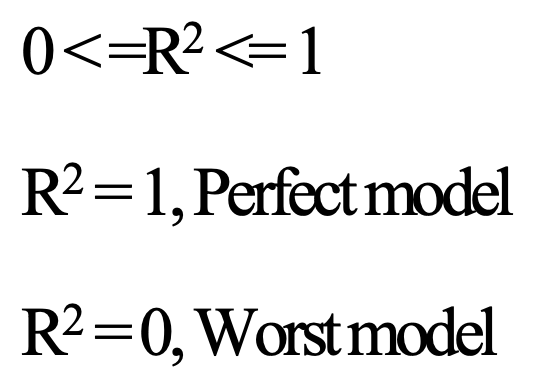
R2 은 0에서 1 사이의 값을 갖고 1에 가까울수록 더 좋은 모델을 의미한다.

실제로 데이터의 분포에 따라 결정계수가 어떻게 나오는지를 살펴보자.

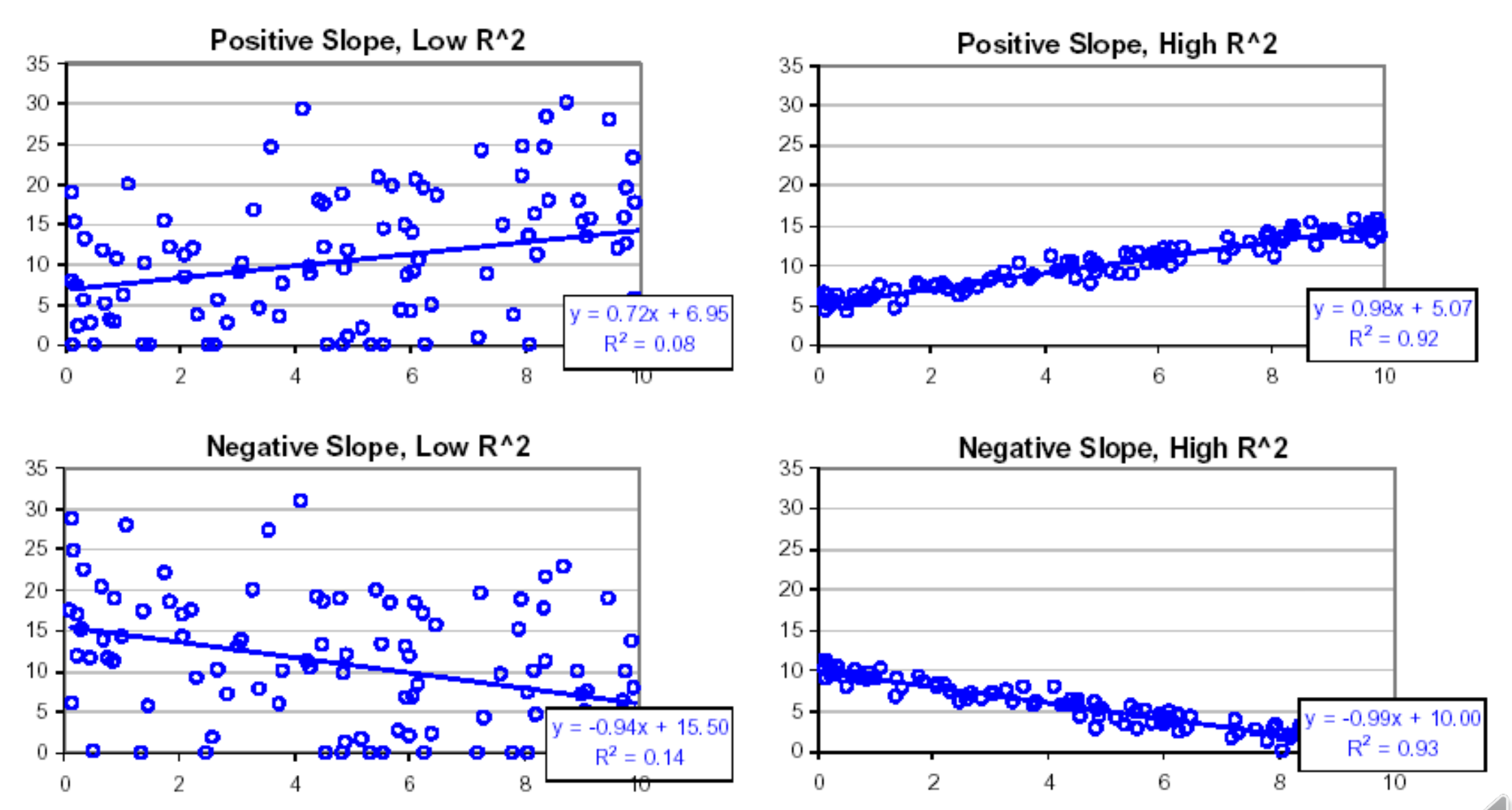
좌측의 두 그래프는 결정계수가 0에 가깝고, 우측의 두 그래프는 1에 가깝다. 그만큼 선형회귀모델이 실제 데이터에 적합한 모델이라는 것을 알 수 있다. 값의 분포를 보면 데이터가 모여있지 않고 흩뿌려져 있어서 편차 자체가 큰 것을 알 수 있다. 따라서 분모에 들어가는 SST 가 커지고 0에 가까운 결과를 갖는 것이다.

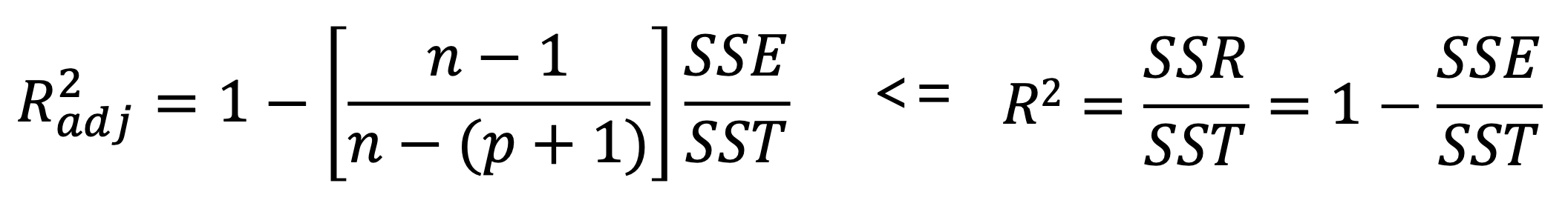
하지만 결정계수를 성능 평가 지표로 사용하기 위해서 중요한 것이 하나가 있는데 바로 변수의 개수이다. 우리가 Input 으로 넣어준 변수가 많으면 많을수록 실제 데이터에 Fitting 이 될 것이다. 가령 데이터가 100개가 있는데 변수가 100개다? 모델이 데이터 그 자체가 되어버려 Test Data 를 설명할 수 없는 Overfitting 이 되는 상황이 나오게 된다. 따라서 가능한 적은 변수로 최고의 성능을 도출하는 것이 핵심이다. 이를 반영한 것이 R2 adjusted 이다. 수집한 데이터의 개수와 변수의 개수를 R2 에 반영했다.

Regularized Regression

단순히 모델의 성능을 높이기 위해 Error 를 줄이는 쪽으로 모델을 구현하다보면 모델이 Training Data 자체가 되어버려 Test Data 를 설명하지 못하는, Overfitting 되는 상황이 발생할 수 있다.

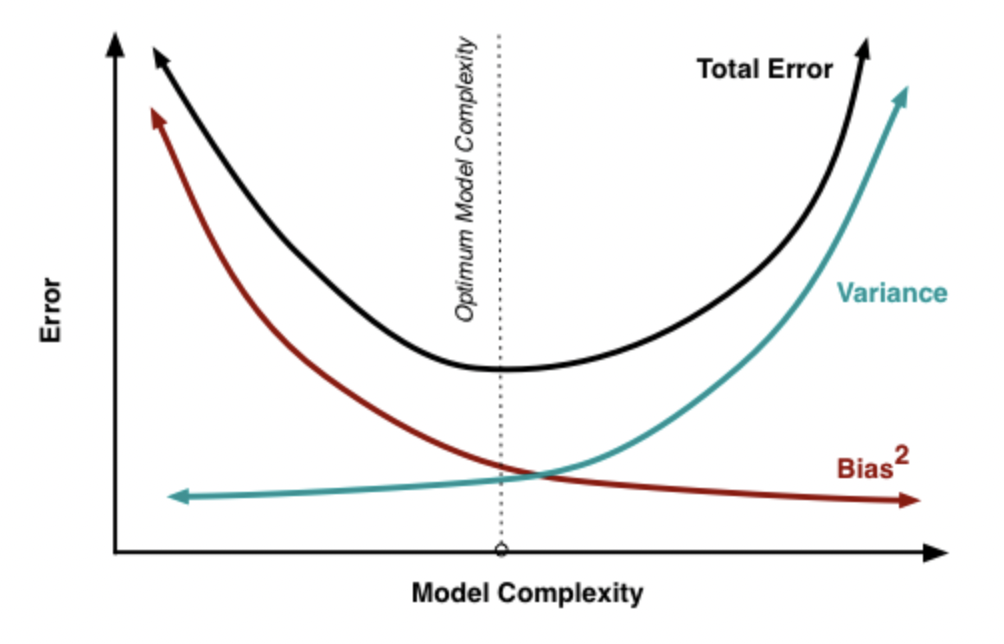
이를 해결하기 위해 Variance 와 Bias 를 가지고 모델을 신경쓰겠다는 것.

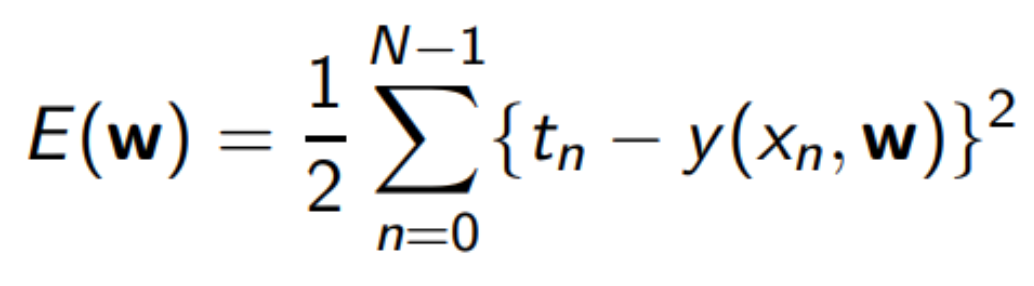
이건 일반적인 MSE

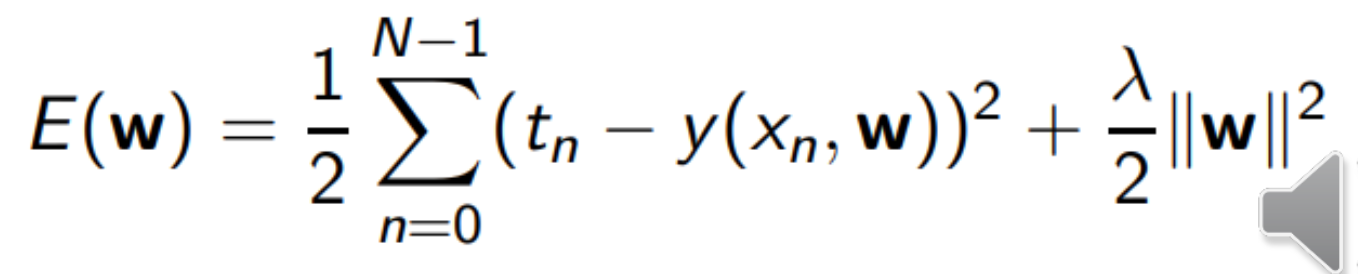
계수의 가중치를 부과한 MSE

장점

1. 유일해를 가지므로 항상 똑같은 결과가 도출된다.
2. 대중적이고 사용하기 쉽다.
3. 설명력이 좋다.
   
   가령 이러한 선형방정식을 구했을 때, Input 에 따라 Output 을 정량적으로 해석할 수 있다. "수확기 강수량이 낮아지고 당해 년도 평균 기온이 올라가면 수치상으로 몇 정도가 좋아진다" 이런 식의 정량적 해석이 가능하다는 장점이 있다.

단점

1. 선형 관계만 설명할 수 있다.
2. Input 에 무의미하거나 중복되는 값이 있는 경우 모델 성능이 저하된다.
3. Goodness of fit 과 prediction power 가 좋지 않다. 선형 관계만 탐색하기 때문이다. (현실 세계에선 비선형적인 관계가 더 많다.)

Nonlinear Regression

Training Data 를 설명하는 모델이 선형적인 형태가 아니라 비선형적인 형태일 떄 Nonlinear Regression 이라고 한다.

장점

• 선형모델에 비해서 더 좋은 성능을 보인다.

단점

• 모델의 복잡도가 올라간다.

• 선형모델에 비해서 설명력이 낮아진다.