충남대학교 컴퓨터융합학부의 김동일 교수님의 기계학습을 수강한 후 정리한 글입니다.
Bayesian Classifier 에 대해 설명하기 전에 예시를 들어보려고 한다.
Salmon - Sea bass Problem
간단한 분류 문제이다. 바다에서 어부가 물고기를 잡는데 연어와 농어가 같이 잡힌다. 이를 분류하려고 한다. 어떻게 분류할 수 있을까?
- 사람이 직접 분류
- 기계가 자동으로 분류
누가봐도 2번이 효율적으로 보인다. 하지만 2번을 사용하기 위해선 기계가 정확하게 분류할 수 있도록 분류 기준이 필요하다. 분류 기준은 여러 가지가 될 수 있다. 가령 물고기의 길이, 밝기, 너비 등등...

컨베이어 벨트 위를 지나가는 물고기를 카메라를 통해서 촬영하고 특성에 관한 데이터를 수집하여 연어와 농어를 분류할 수 있는 모델 을 만들어야 한다.
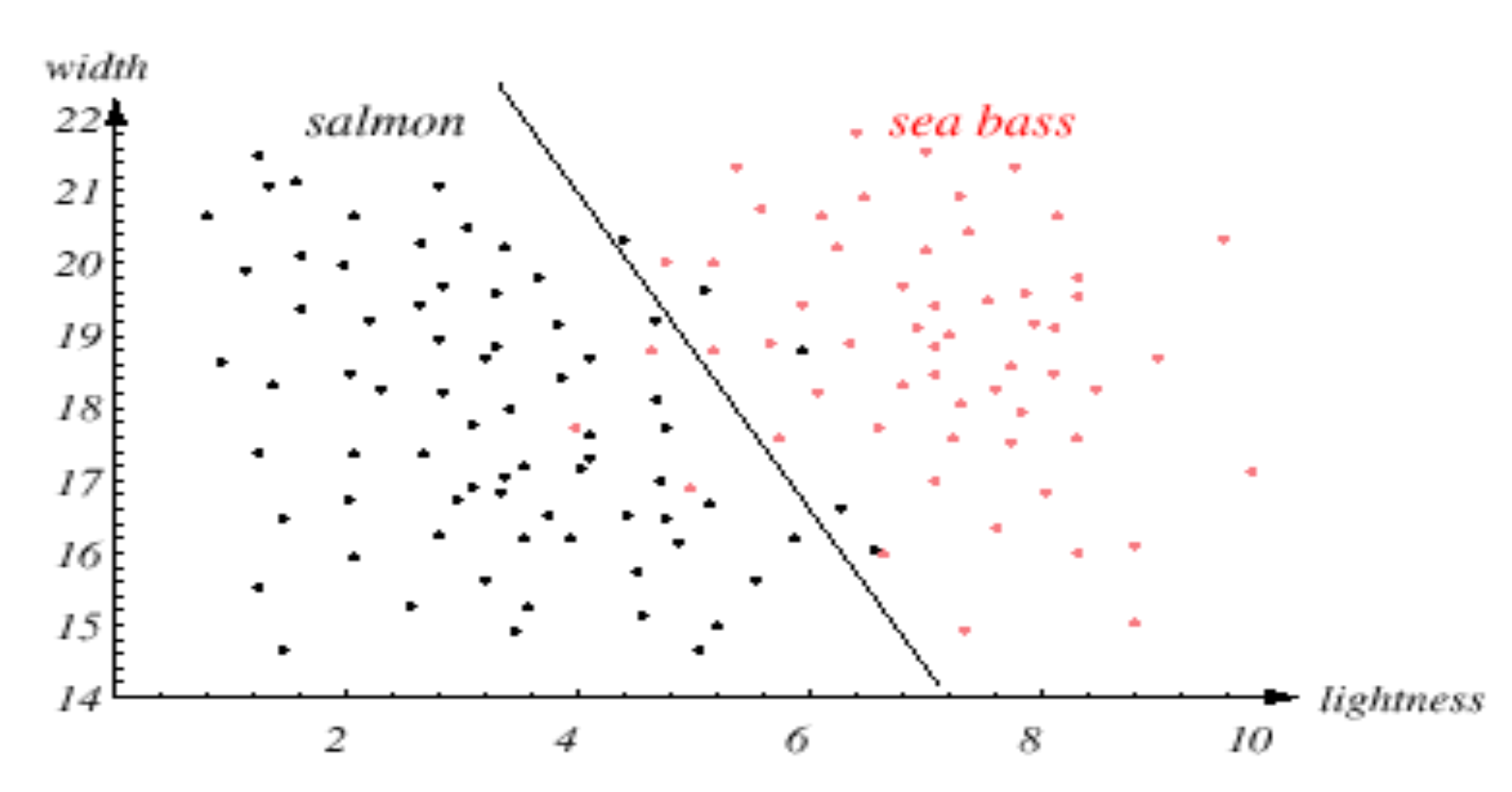
잡은 물고기에 대한 너비 와 밝기 에 대한 데이터를 수집하고 이를 출력해본 결과 위와 같은 분포가 나타났다고 하자. 연어와 농어를 가장 잘 분류할 수 있는 경계선, Class Boundary 를 찾는 것이 우리의 목표다.
Bayesian Classifier
정의
위에서 얘기했지만 우리가 원하는 것은 물고기를 잡았을 때 잡은 물고기 중에 연어가 얼마나있냐가 핵심이다. 즉 어떤 Data(x) 가 있을 때 W 클래스에 속할 확률을 구하는 것이고 이는 결국 조건부확률 을 뜻한다.


조건부확률 은 위와 같이 표현할 수 있다.
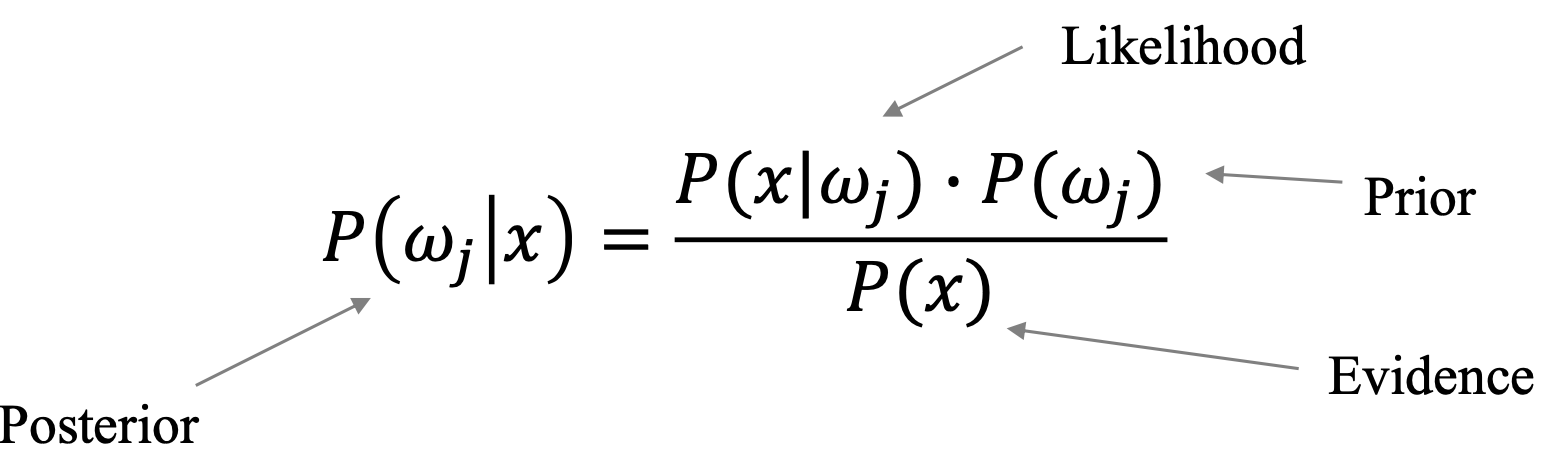
각각에 대한 설명을 해보자면,
-
Likelihood : 우도
데이터에서 추출한 각 클래스의 분포 -
Prior : 사전확률
베이시안 분류의 핵심이며 다른 모델들과 차이를 갖는 핵심 요소이다. 수집한 데이터, 즉Training Data와는 관계 없이 자연 자체에 존재하는 확률이다. -
Evidence : 증거
수집한 전체 데이터 -
Posterior : 사후 확률
우리가 계산하려는 확률
그렇다면 likelihood 에 prior 를 곱해주는 이유가 무엇일까?
이것도 예를 들어 설명해보겠다.
노르웨이 앞바다에 연어와 농어만 서식한다고 가정하고, 연어가 잡힐 확률은 2/3, 농어가 잡힐 확률은 1/3 이다. 현재 물고기를 한 마리 잡았고 이 물고기가 무엇인지 맞춘다면 100억을 준다고 했을 때 연어와 농어 중에 어떤 것을 택할 것인가? 당연히 연어다. 통계상으로 실제로 더 많이 존재하기 때문이다. 잡은 물고기가 실제로 무엇인지는 모르지만 통계상으로 더 많이 존재하기 때문에 우리는 연어를 택하게 된다. 우리는 어떠한 판단을 할 때, 현재의 데이터를 기반으로 선택함과 동시에 과거의 데이터도 확인한다. 가령 연어와 농어의 likelihood 가 각각 0.5로 같아서 두 종류를 명확하게 분류할 수 없다면 이 때 사전 확률, prior 를 개입시키면서 이를 확실하게 분류하겠다는 뜻이다.
Minimize Error

확률에 따라 특정 클래스를 선택했다면 선택하지 않은 클래스의 확률은 Error 가 된다. 이러한 Error 를 최소화하는 것이 우리의 목표다.
Bayesian Classifier은likelihood에prior를 개입시켜error를 최소화하는posterior를 계산한다는 것이다.
지금까지 Bayesian Classifier 의 개념에 대해 알아봤다. 지금부터는 Bayesian Classifier 를 적용해서 어떻게 클래스를 분류할 것인지에 대해 알아볼 것이다.
적용
우선 가정이 필요하다. 수집한 데이터들은 가우시안 정규 분포를 만족한다고 가정한다. 아래는 가우시안 분포이다.
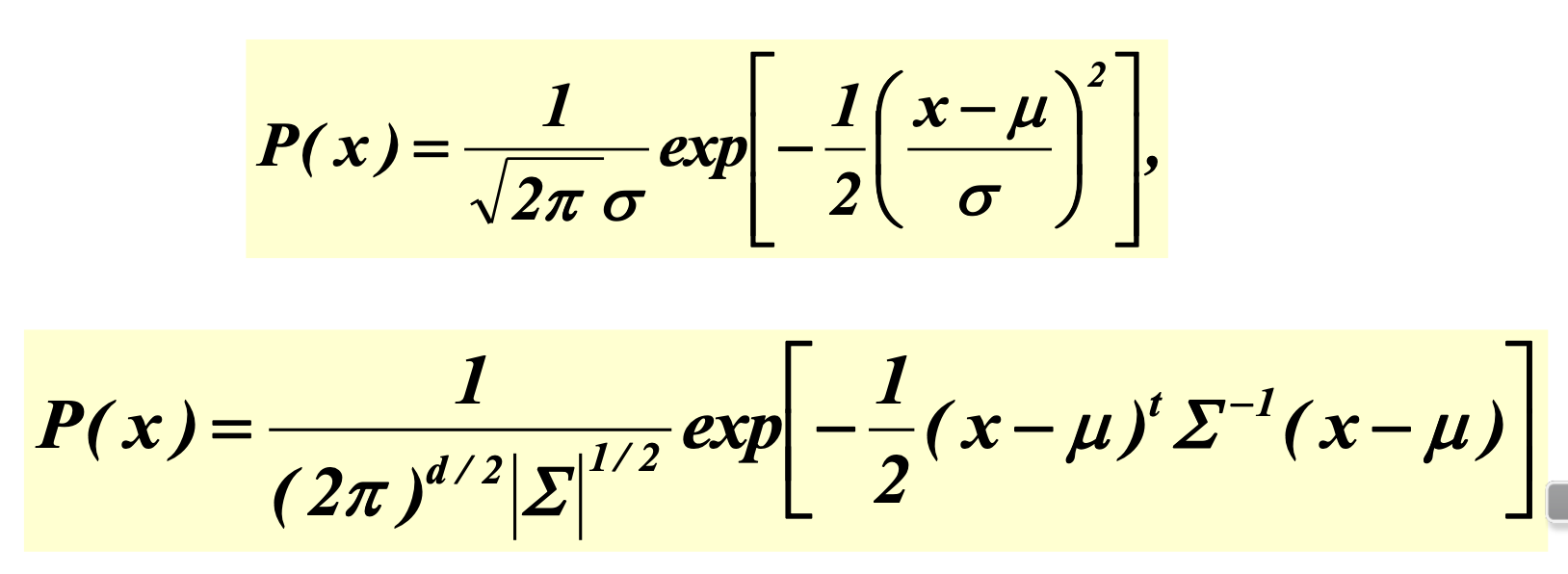
가우시안 정규 분포를 만족하면 이런 식을 만족하고 우리는 식에 들어가는 평균과 분산을 찾아야한다. 위에 있는 식은 단변량 일 때의 가우시안 정규분포식이고 아래에 있는 식은다변량 일 때의 가우시안 정규분포식이다.
Univariate(단변량)은 뭐고, Multivariate(다변량)은 뭐에요?
단변량은 Feature 가 1개, 다변량은 Feature 가 여러 개일때를 의미한다. Salmon - Sea bass 문제에서는 너비와 밝기, 두 개의 특징을 가지고 추정했으므로 다변량에 해당한다.
하지만 Bayesian Classifier 에는 가장 중요한 가정이 있는데 이는 아래에서 설명하도록 하겠다. Bayesian Classifier 의 핵심이라고도 볼 수 있는 이 가정 덕분에 평균과 분산을 쉽게 구할 수 있게 된다.
그럼 가우시안 분포를 만족하는 평균과 분산을 찾아보자.
우선 그 전에 로그함수의 특징에 대해 알아야한다.
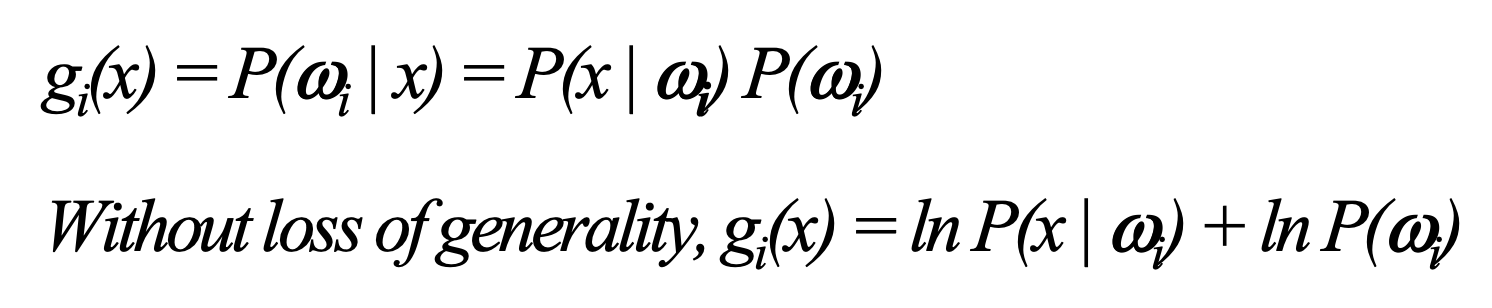
로그 함수는 항상 양수이기에 로그 함수를 나눠줘도 대소 관계에는 변함이 없다. 두 번째 식에 로그를 씌어주면 아래와 같은 결과가 나온다.
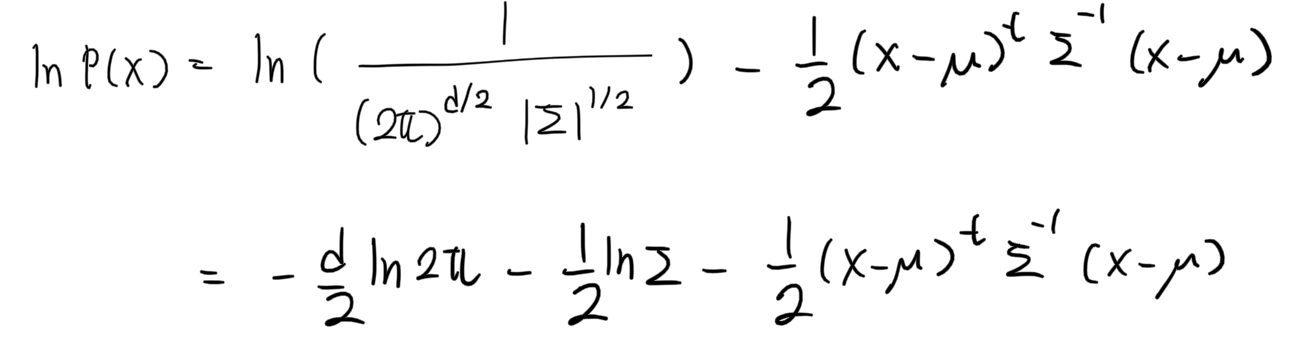
식은 이렇게 정리가 됐고, 우리가 찾아야 하는 것은 평균 과 분산 이다. 아까 위에서 말했던 것처럼 평균과 분산을 찾되, Posterior 가 최대가 되도록 해야한다. 어떻게 구할 수 있을까? 정답은 미분이다.
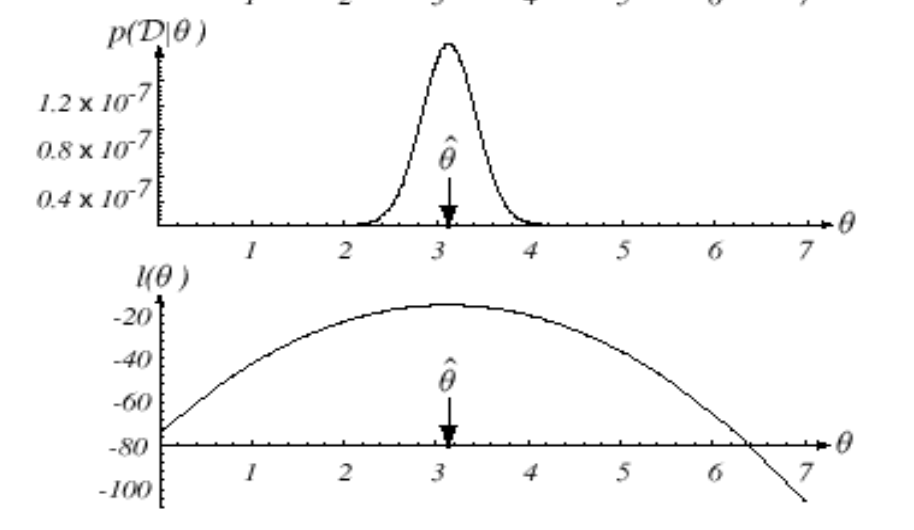
likelihood 는 위와 같은 그래프를 가지므로 최대값에서 미분 값은 0이다. 따라서 위에서 구한 식을 평균 과 분산 에 대해 미분하고 0을 만족하는 값을 찾으면 된다.
1. 평균을 모르고, 분산을 알고 있을 때
평균은 모르고 분산을 알고 있으므로 분산이 들어간 식은 상수가 된다. 평균을 미지수로 놓고 평균에 대해 미분을 하면 아래와 같은 식이 나온다.
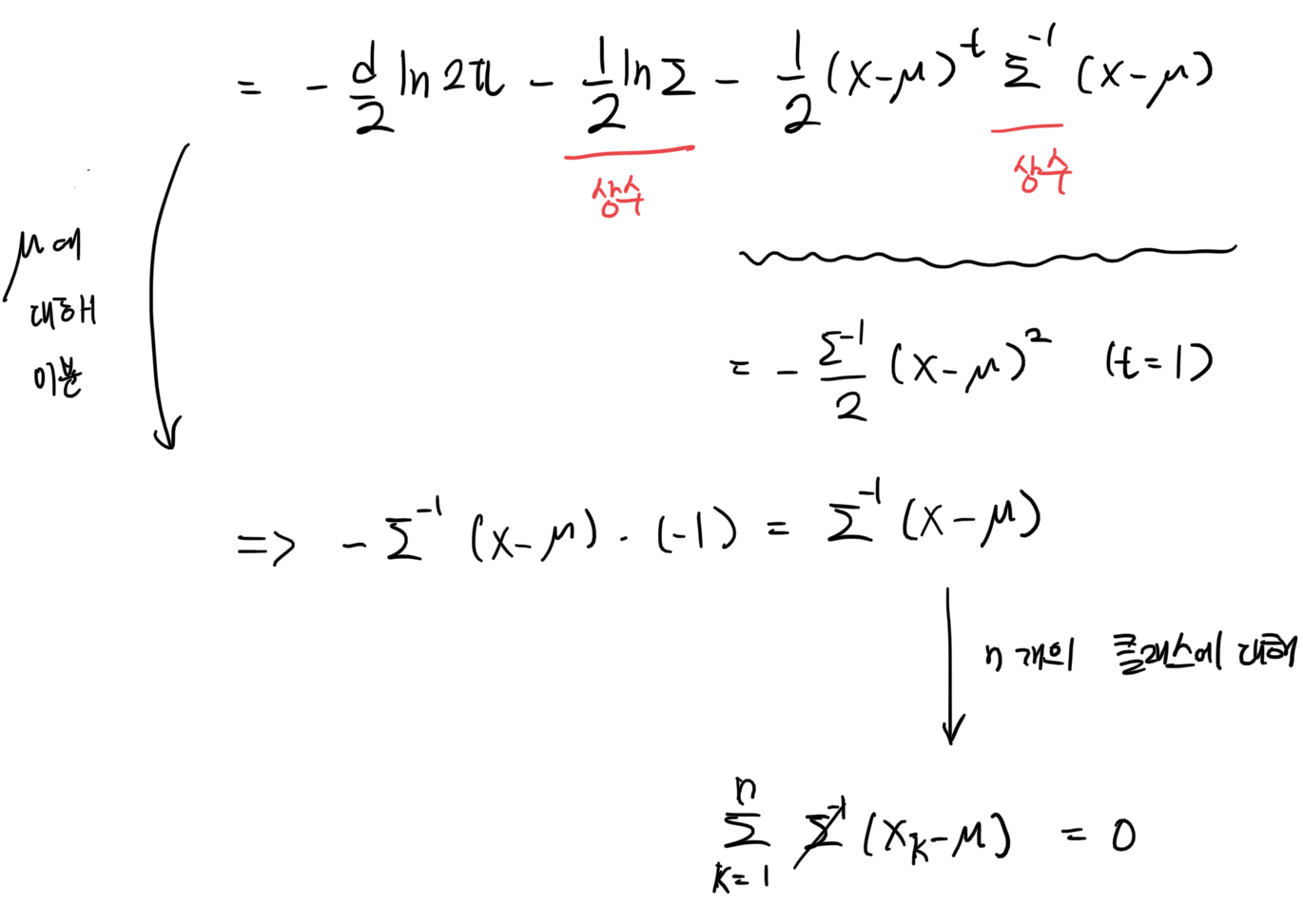
어디서 많이 본 듯한 값이다. 아직 모르겠다면 식을 좀 더 풀어보겠다. 분산은 지금 알고있으므로 상수이고, 따라서 나눠줄 수 있다.
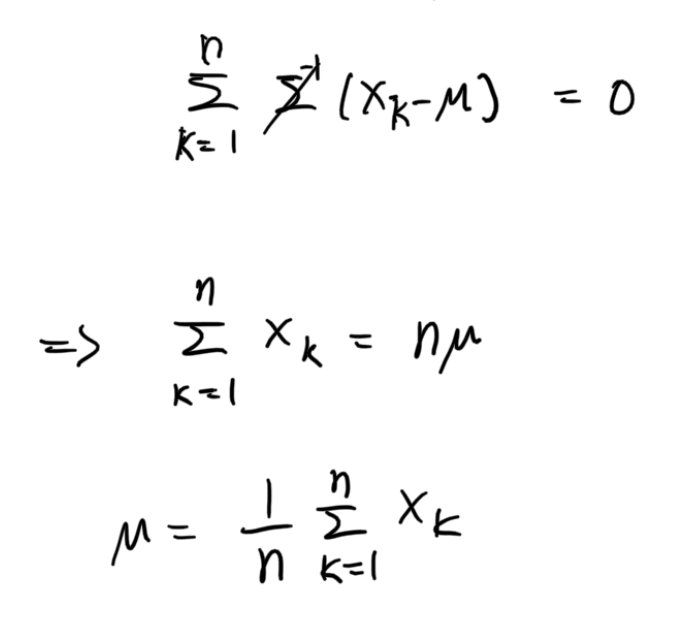
뭔가 엄청 어렵고 복잡하게 구한했는데 결과는 간단하다. 우리가 흔히 알고 있는 평균, 산술 평균 이다. 어떻게 보면 당연하다. 우리가 수집한 데이터가 애초에 가우시안 정규 분포를 만족한다고 가정했으므로 평균은 당연히 산술 평균이 나오는 것이다.
2. 평균과 분산을 모두 모를 때
평균과 분산을 모두 모르므로, 평균과 분산을 각각 미지수로 놓고 미분을 진행해야 한다. 평균을 구하는 식은 이미 위에서 구했으므로 생략하겠다. 분산에 대해 미분을 진행하면 아래와 같은 식이 나온다.

최종적으로 나온 값 역시 어디서 많이 본 결과이다. 우리가 알고 있는 분산, 편차 제곱의 합 이다. 어렵게 식을 전개하면서 구했는데 결과는 동일하다. 모델이 정규분포를 만족한다고 가정했기 때문에 이런 결과가 나오는 것이다.
중요!
하지만 각 변수 간에는 연관 관계가 있다. 물고기의 길이와 너비는 분명히 연관이 있을 것이다. 이런 경우 Feature 의 공분산을 계산해줘야하는데 결과적으로 식이 너무 복잡해진다. 따라서 각 변수들이 서로 독립적이라는 가정을 넣어주는데 이를 Naive Bayesian 라고 하며 일반적으로 얘기하는 Bayesian 이 된다. Multivariate 문제를 Univariate 문제로 접근하는 느낌이다. 이는 Bayesian Classifier 에서 가장 중요한 가정이다.
정리
Bayesian Classifier 은 사전 확률과 우도를 가지고 새로 들어온 데이터가 무엇인지를 확률적으로 예측하는 것이다. 이는 가장 큰 likelihood 를 가질 떄의 class boundary 를 찾는 것을 의미한다. 또한 Bayesian Classifier 는 Generative 하고 Parametic 하다는 특징이 있다.