충남대학교 컴퓨터융합학부의 김동일 교수님의 기계학습을 수강한 후 정리한 글입니다.
Bayesian ClassificationLinear RegressionLogistic RegressionK-NN Classification- Model Evalutation
오늘은 모델을 평가하는 방법에 대해 얘기를 해보려고 한다.
Model Evaluation
모델을 구축하는 과정은 Training Data 를 통한 Fitting 이후 Test Data(Unseen Data) 를 통한 Generalize 을 거친다. 다시 말해, 학습 데이터로 모델을 만들고 이 모델을 테스트하는 과정을 거친다. 테스트 데이터를 더욱 잘 설명하는 모델이 좋은 모델이다. 이를 판단하는 기준은 Error 이다. 실제 값과 예측 값과의 차이를 의미하기 떄문이다. 따라서 Error 가 더 작은 Fit 한 모델을 만들어야 한다.
하지만 단순히 Error가 0에 가깝다하여 좋은 모델이라고 말할 수 있을까?
그렇지 않다. Fit 한 모델을 만들면 당장 Training Data 에 대해선 잘 설명할 수 있다. 하지만 Test Data 가 들어오는 경우 모델 자체가 Training Data 에 일반화되어있기 때문에 새로운 데이터에 대해선 설명할 수 없는 결과가 나온다. 학습 데이터 자체를 외워버렸다고 생각하면 된다. 이를 Overfitting 이라고 한다.
Underfitting, Overfitting
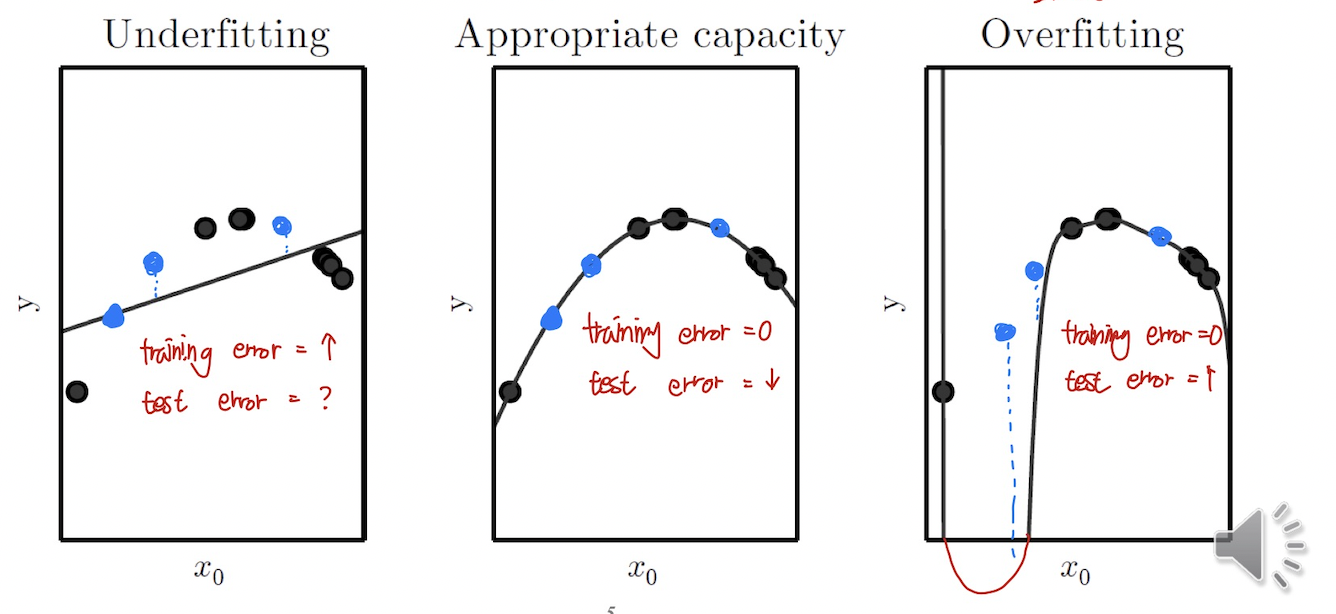
검은색 포인트를 Training Data, 파란색 포인트를 Test Data 라고 하자.
좌측은 Linear Regression, 우측은 높은 차수의 Nonlinear Regression 으로 모델을 구축했다.
우선 Training Error 부터 살펴보자.
좌측의 경우 Training Error 부터 높게 출력되는 것을 볼 수 있다. 이와 다르게 나머지 2개는 Training Error 가 0인 것을 볼 수 있다.
이번엔 Test Error 를 살펴보자.
좌측의 경우 Training 자체가 덜 되어있는 모델이었고, 따라서 Test Error 역시 높게 나온다. 나머지 2개의 경우 Training Error 와 다르게 우측 모델에서는 Overfitting 이 발생해서 Test Error 가 더 크게 나오는 것을 볼 수 있다.
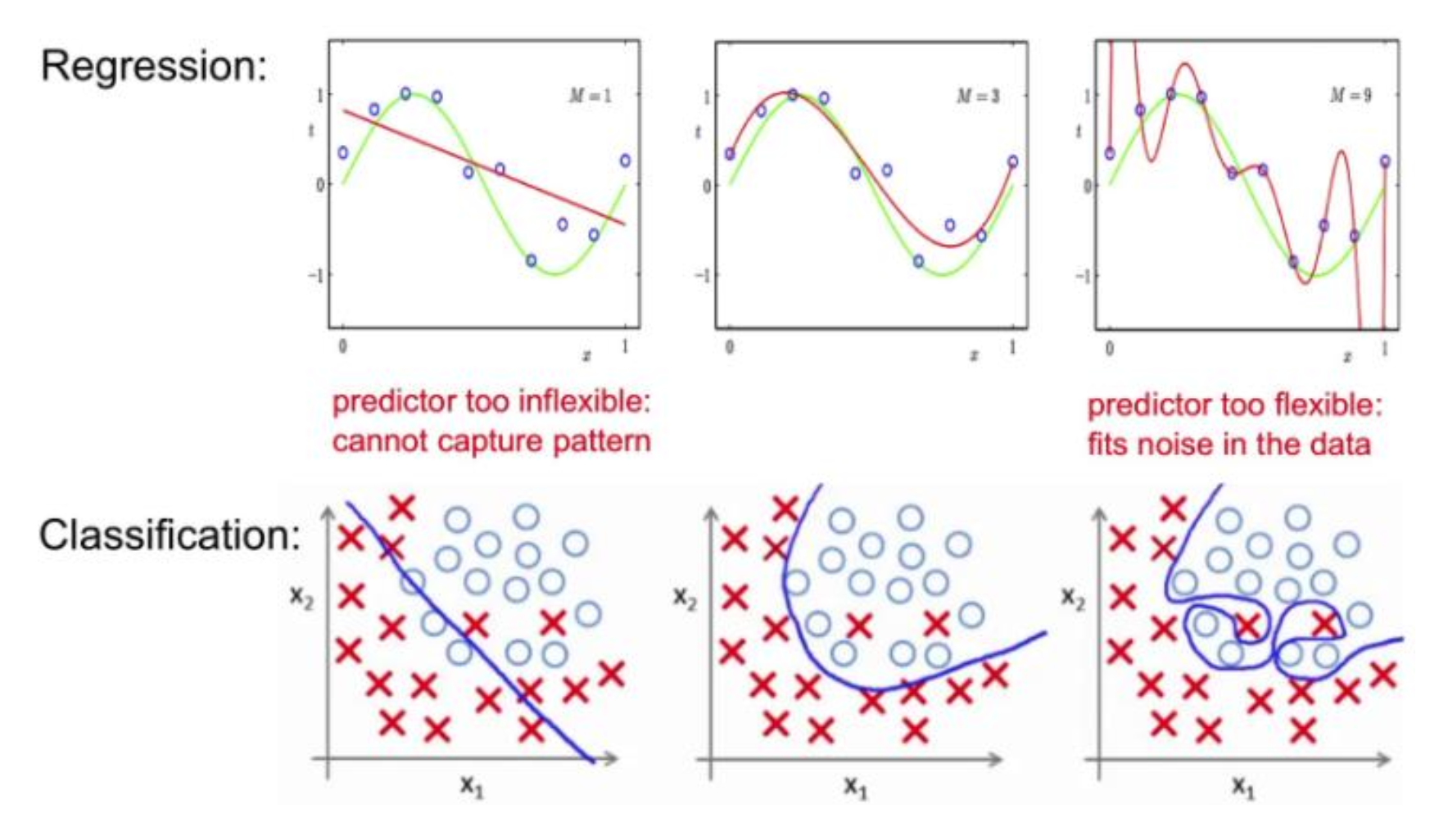
또 다른 예시를 살펴보자. 이전 예시와 마찬가지로 가운데와 우측 모두Training Error 는 두 모델 모두 0에 가깝지만 Test Error 는 우측 모델에서 더 큰 것을 볼 수 있다.
두 개의 예시가 의미하는 바는 무엇일까? Appropriate와Overfitting 을 Training Data 로는 판별할 수 없다는 것을 의미한다. 오직 Test Data 를 통해서 Overfitting 여부를 판단하는 것이다.
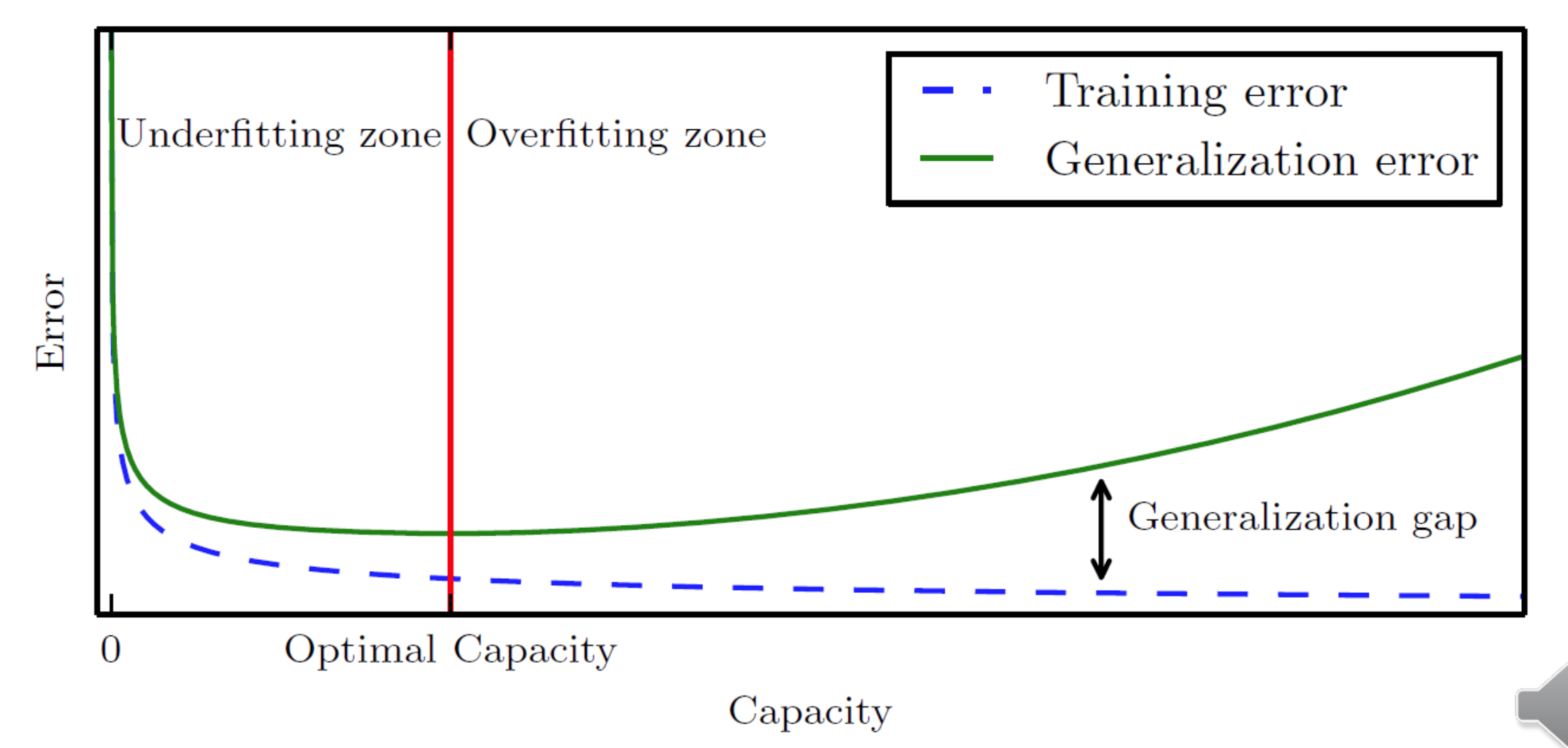
모델의 복잡도가 올라갈수록 Training Error 는 0에 수렴한다는 것을 위에서 설명했다. 하지만 반대로 Test Error 는 올라간다. Training Data 자체를 외워버리는 상황이 발생하는 것이다. 따라서 Training Error 와 Test Error 를 모델 평가의 기준으로 삼을 것이다. Optimal Capacity 를 찾는 것이 우리의 목표다.
Evaluation Method
모델을 검증하고 싶은데 어떻게 검증할 수 있을까?
Data Partitioning 과 K-Fold Cross Validation 을 알아보자.
Data Partition
Data 를 Training Data , Validation Data , Test Data 로 분류하는 것이다.
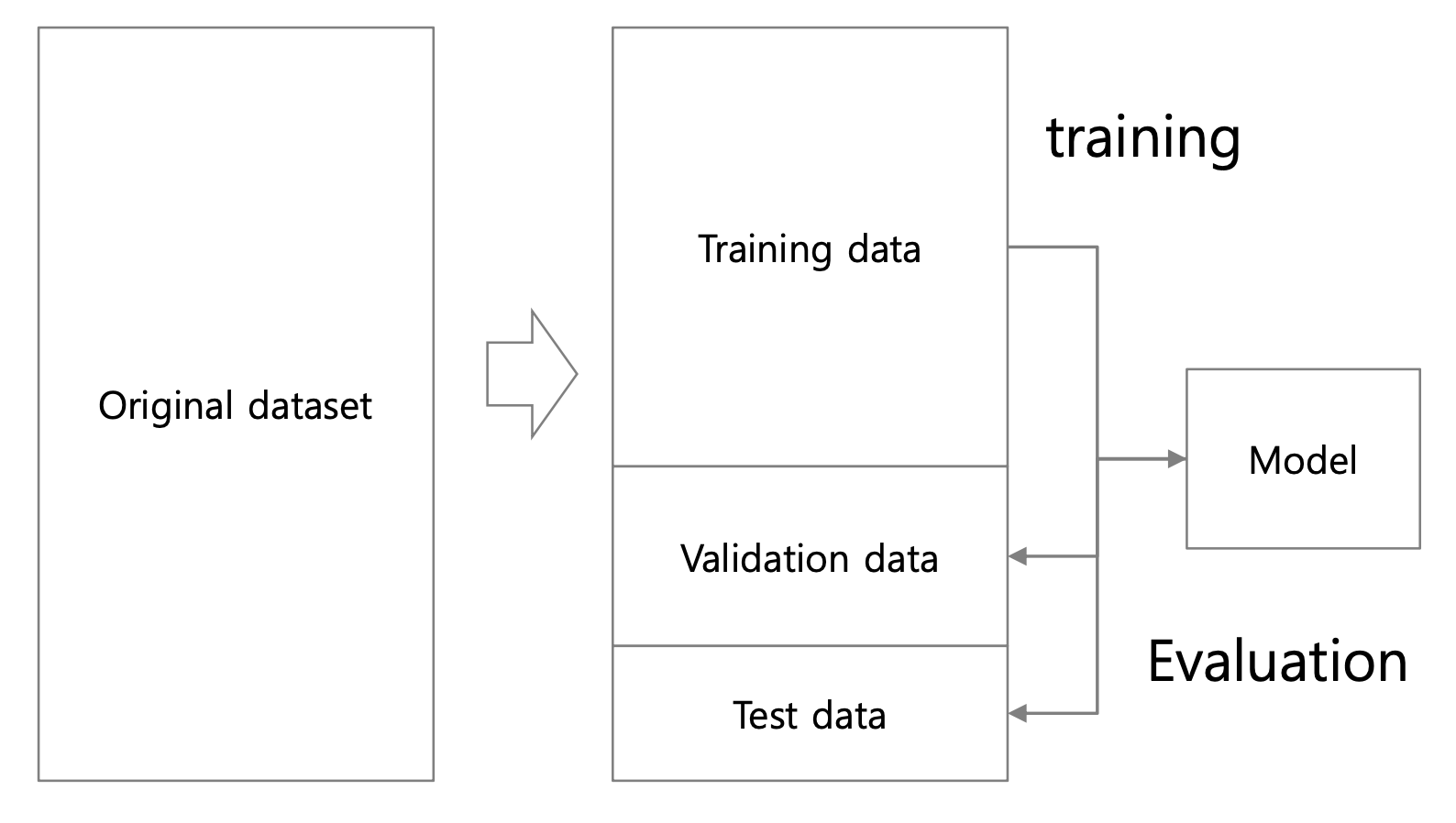
Trainging Data로 모델을 학습시킨다.Validation Data로 모델을 평가한다.Test Data로 모델을 한번 더 평가한다.
우선 Validation Data 로 모델을 평가하는 이유는 Overfitting 여부를 판단하기 위해서이다. 모델이 Training Data 를 외워버리는 상황, 즉 Training Data 에 bias 되는 것을 막기 위한 과정이다.
마지막으로 Test Data 로 한번 더 평가하는 이유는 정말 낮은 확률이지만 Validation Data 가 Training Data 와 정말 비슷한 값일수도 있다. 이때 Validation Data 에 bias 되는 것을 막기 위한 과정이다.
K-Fold Cross Validation
Data Partitioning 과 다른 방법이다. Data Partitioning 에서 Partitioning bias 가 발생할 수 있는데 이를 해결할 수 있다. 또한 데이터 수가 적은 경우에 활용하면 좋다.
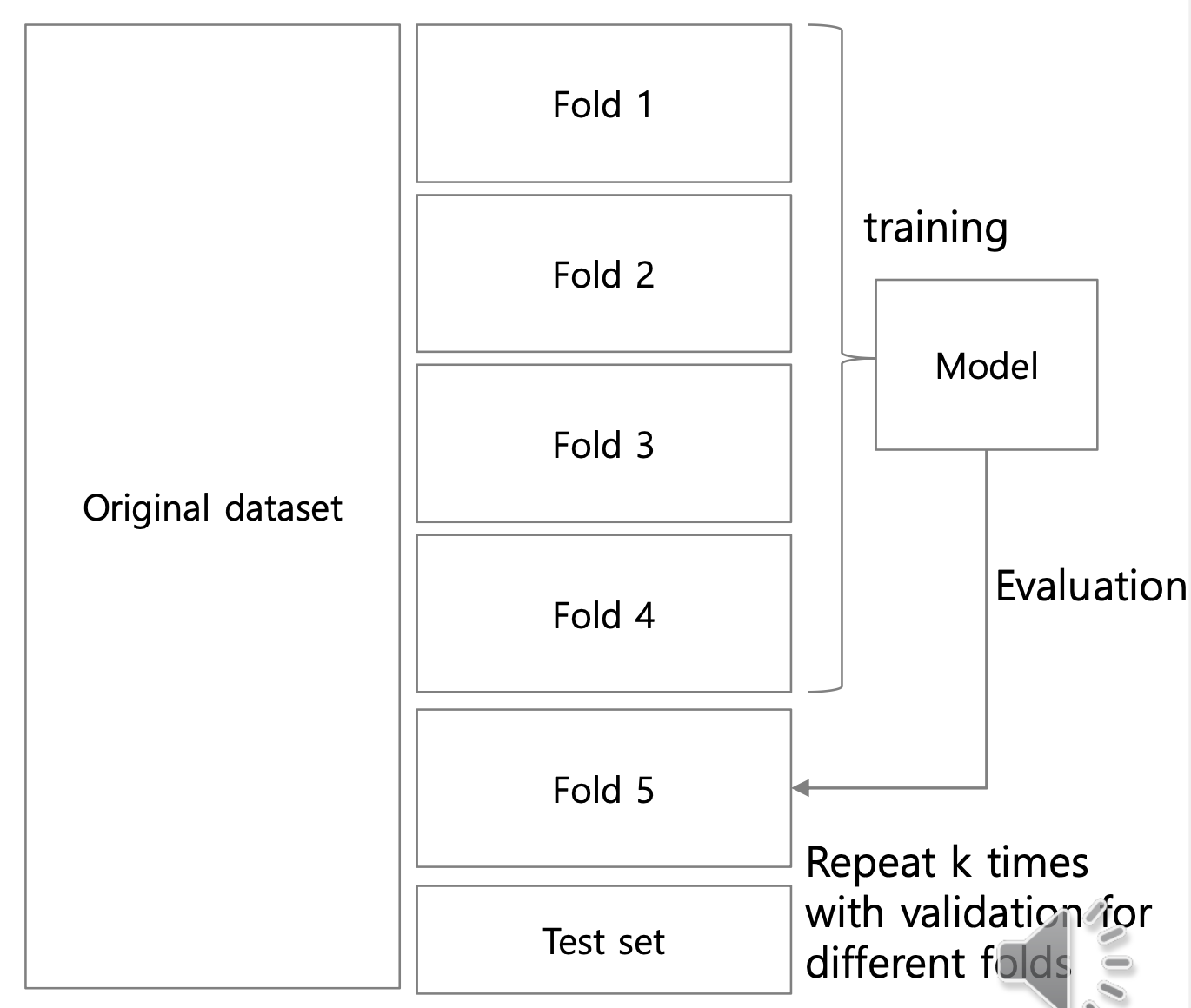
- 우선
Training Data와Test Data를 나눈다. Training Data을 N등분 한다. 이를fold라고 한다.- 각
fold를 한번 더 N등분한다. N-1개를Training Data,1개를Test Data로 사용한다.
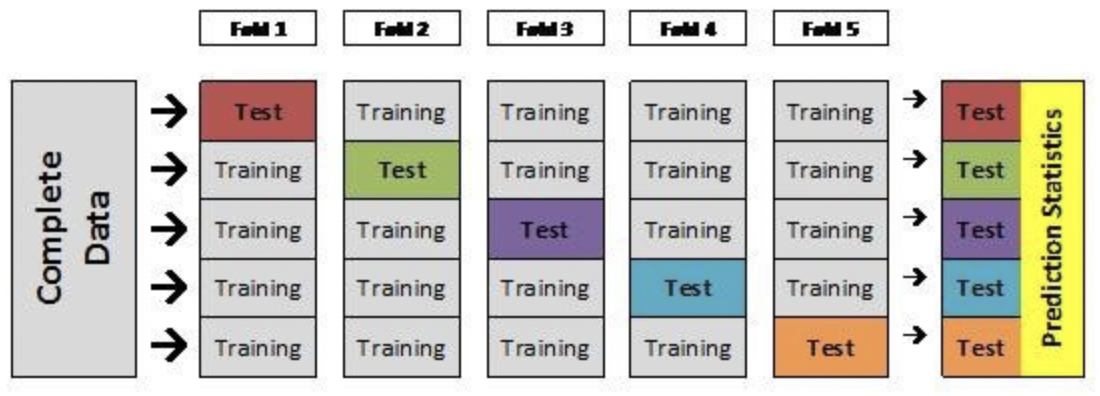
더 이해하기 쉬운 그림이 있어서 들고왔다. k-fold 연산 결과 각 fold 는 N-1 번의 Training data , 1 번의 Validation Data 로 사용된다.
Regularization
위에서 말했던 것처럼 단순히 Error 만 줄이는 것은 Overfitting 을 발생시킬 수 있다. 따라서 Error 와 Complexity 를 모두 고려하여 Optimal Capacity 를 찾아야 한다.
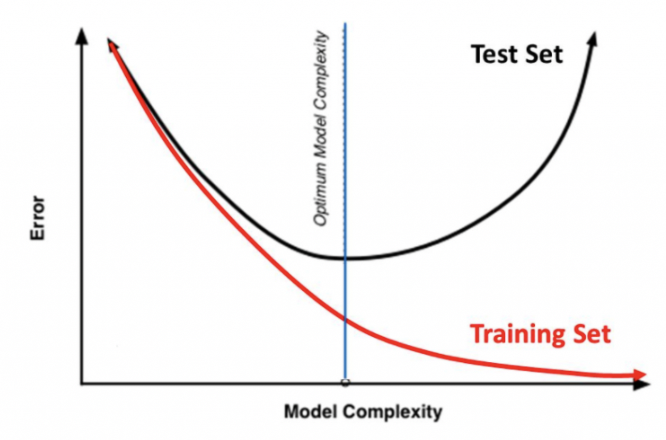
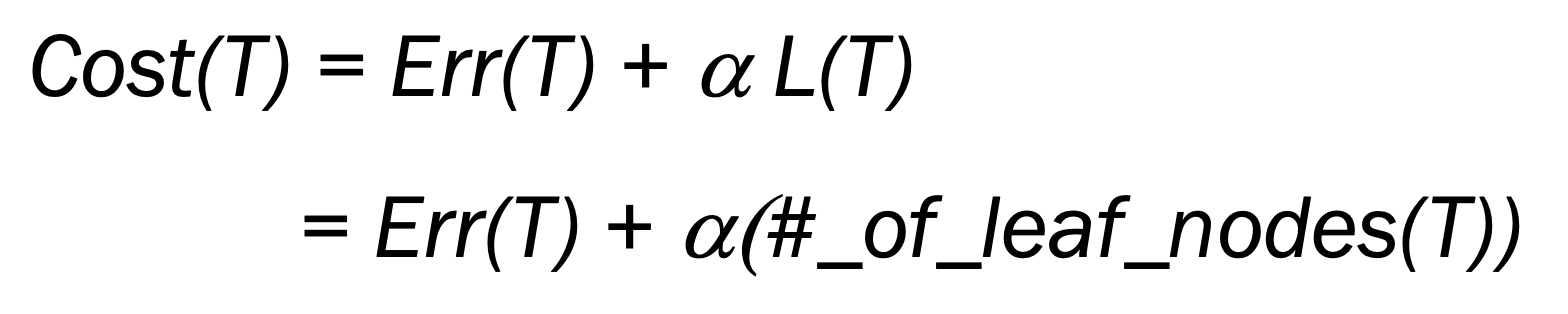
Error 와 Complexity 의 관계는 시소와 같다. 일단 궁극적인 목표는 Cost 를 최소화하는 것이고 Cost = Error + a*Complexity 을 만족한다. 이때 Hyper-parameter 인 a 를 어떻게 설정하냐에 따라 어디에 초점을 맞출지가 정해진다.
만약 a 를 크게하면 Complexity 에 따라 Cost 가 급격하게 변한다. 따라서 Complexity 를 최소화하는 쪽으로 초점을 맞춘다. Underfitting 이 발생할 수 있다. 이와 반대로 a 를 작게하면 Error 에 따라 Cost 가 변한다. 따라서 Error 최소화하는 쪽으로 초점을 맞춘다. Overfitting 이 발생할 수 있다.
Ridge Regression (L2)
MSE 가 가장 큰 변수를 제거하는 역할을 한다.
Lasso Regression (L1)
Weight 를 0으로 만들어서 불필요한 변수를 제거하는 역할을 한다.
Evaluation
우리는 정확도로 모델을 평가할 수 있다. 하지만 정확도로 모든 것을 판별하기에는 무리가 있다. 각 모델에 따라 Misclassification cost 이 다르기 때문이다.
Misclassification cost
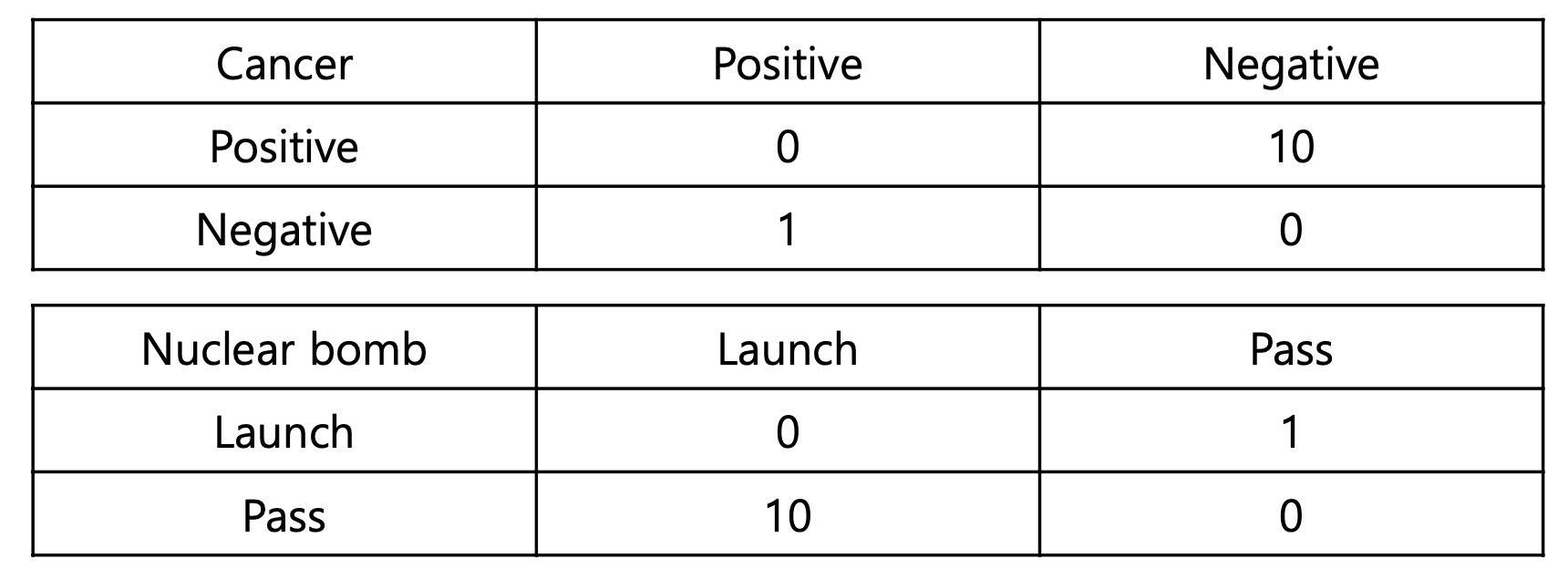
우선 첫번째 사례부터 살펴보자. 가로가 예측이고 세로가 실제이다. 우선 정확도가 0이다.
-
실제로 양성인데 예측은 음성으로 한 경우 (Pos -> Neg)
최악의 상황이다. 실제 암에 걸렸는데 암이 아니라고 말해준 것이기 때문이다. 이를Miss라고 한다. -
실제로 음성인데 예측은 양성으로 한 경우 (Neg -> Pos)
좀 그렇긴하지만 위의 예시보단 괜찮다. 암이 아닌데 암이라고 말해준 것이디 때문이다. 이를False라고 한다.
만약 Miss 가 False 보다 큰 경우 더 민감한 모델이 필요하다.
-
실제로 발사를 해야하는데 그냥 지나친 경우 (Pos -> Neg)
상황이 적합한지는 모르겠는데 아군이 피해를 볼 수 있다. 이를Miss라고 한다. -
실제로 발사하면 안되는데 발사를 한 경우 (Neg -> Pos)
쏘아올린 작은 핵미사일로 인해 핵전쟁이 시작될 수 있다. 이를False라고 한다.
만약 False 가 Miss 보다 큰 경우 더 둔감한 모델이 필요하다.
이처럼 단순히 정확도로 판별하기에는 세상이 너무 복잡하다. 따라서 정확도 뿐만 아니라 다른 측정 값도 추가했다.
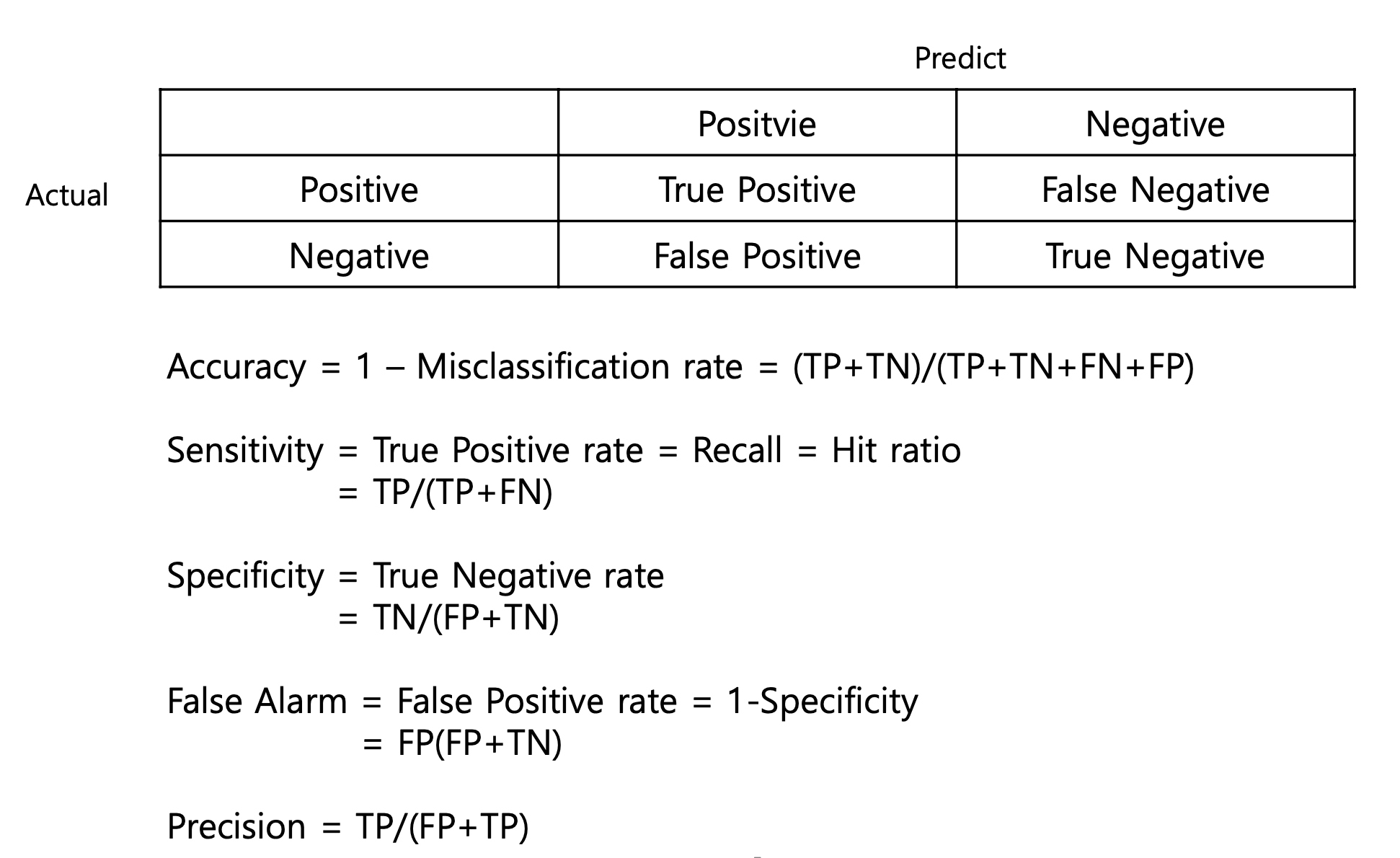
- Accuarcy
- Sensitive : 실제 Positive 중 예측 Positive
- Specificity : 실제 Negative 중 예측 Negative
- False Alarm : 실제 Negative 중 예측 Positive
- Precision : 예측 Positive 중 예측 Positive

또한 F1 이라 하여 Sensitive 와 Precision 의 조화평균으로 계산한 값도 존재한다.
ROC, AUC
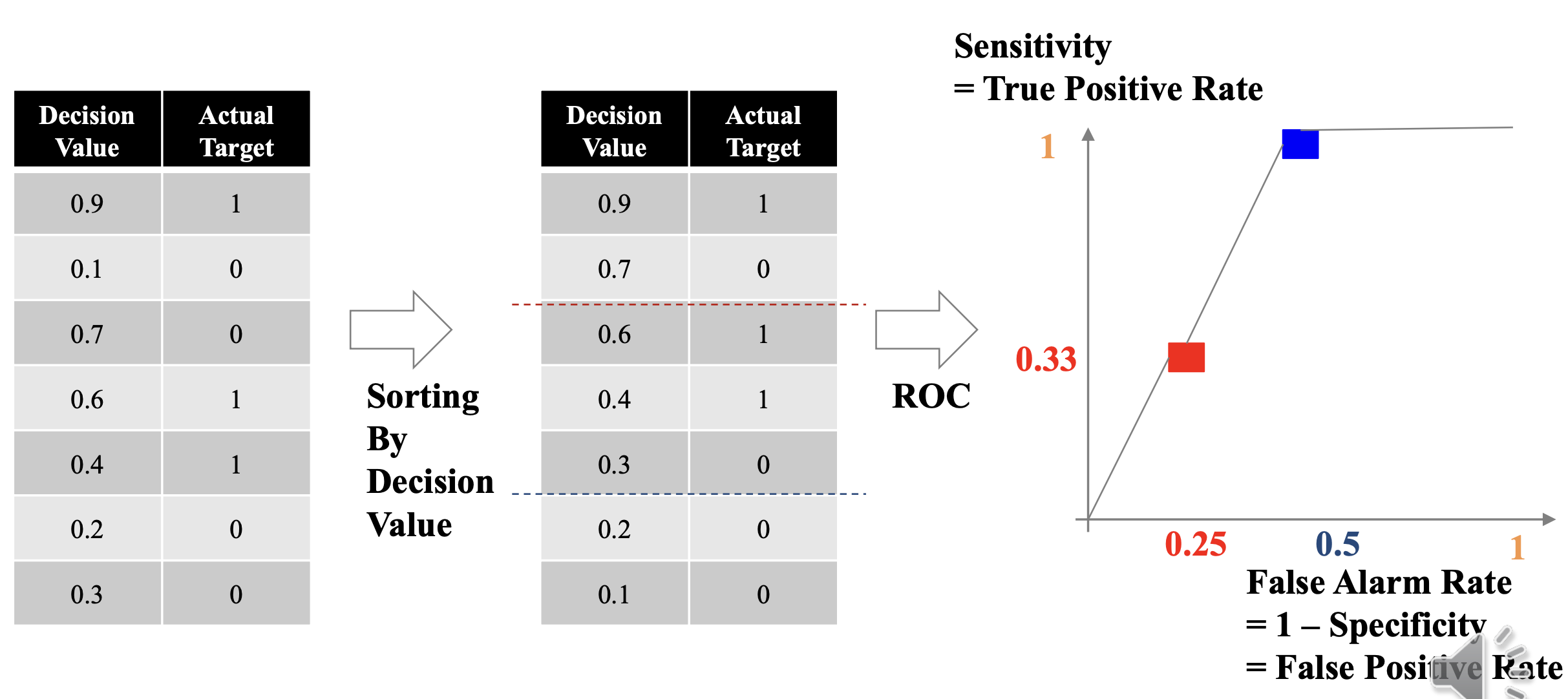
이런 느낌. ROC 를 적분하면 AUC
정리
-
람다가 크다 -> 복잡도의 변화에 큰 반응을 보임 -> 복잡도에 초점을 맞춰 복잡도를 줄이자 -> Underfit
-
람다가 작다 -> 복잡도보다 학습 에러에 더 큰 반응을 보임 -> 학습 에러에 초점을 맞춰 학습 에러를 줄이자 -> Overfit