Machine Learning by professor Andrew Ng in Coursera

Introduction

Learning algorithm (학습 알고리즘) = 지도 학습 알고리즘 + 비지도 학습 알고리즘

Supervised Learning (지도 학습)

정답을 알려주는 경우

• 알고리즘에게 주입하는 훈련데이터 label 이라는 답 을 포함하는 경우
  -> 알고리즘의 역할은 더 많은 '정답'을 만들어 내는 것 (새로 들어올 입력값에 대한 정답 같은 것)
  • Regression (회귀)
    : 연속된 값을 예측 (ex. housing price)
  • Classification (분류)
    : 불연속적인(Discrete) 값을 예측 (ex. breast cancer <- 악성/양성 종양 구분 )

Unsupervised Learning (비지도 학습)

정답이 없는 경우

• 어떤 label도 갖고 있지 않거나 / 모두 같은 label / 아예 label이 없는 경우
• "주어지는 데이터에서 어떤 구조(structure)를 찾을 수 있는가" 를 묻는다.
  • Clustering (클러스터링)
    : 비슷한 것들끼리 한 클러스터로 묶는다.

=> 알고리즘이 스스로 데이터를 통해 구조를 찾도록 한다.

---

Model and Cost Function

Cost Function

• Hypothesis :
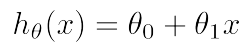
• Parameters : θ들
  새로운 θ들의 조합을 선택할 때마다 새로운 가설이 생긴다.
  비용함수로 파라미터의 값을 결정한다.
• Cost Function : 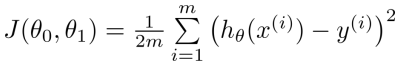이때의 비용함수는 Squared Error,
  다른 비용함수들도 있지만 오차제곱함수가 회귀문제에서는 대체로 사용된다.
• 비용함수를 최소화하는 θ를 찾는 것이 목표

=> 비용함수 J를 최소화하는 θ를 찾으면 그게 곧 훈련데이터를 가장 잘 나타내는 θ가 된다.

---

Parameter Learning

Gradient Descent

• 비용함수 J의 최솟값을 구하는 알고리즘
  선형회귀에서만이 아니라 일반적으로 많이 쓰인다.
  비용함수 뿐만 아니라 다른 함수들의 최솟값을 구할 때에도 쓰인다.

  Gradient descent algorithm

  repeat until convergence:
  
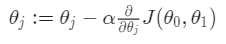
  θ들의 값은 동시에 업데이트 한다.

• α : learning rate
  • α가 작을 때 : 최솟값에 도달하기까지 오래 걸린다.
  • α가 클 때 : 방향전환에 실패하고, 최솟값에서 멀어질 수 있다.
• θ_1이 지역 최솟값에 도달한 경우
  
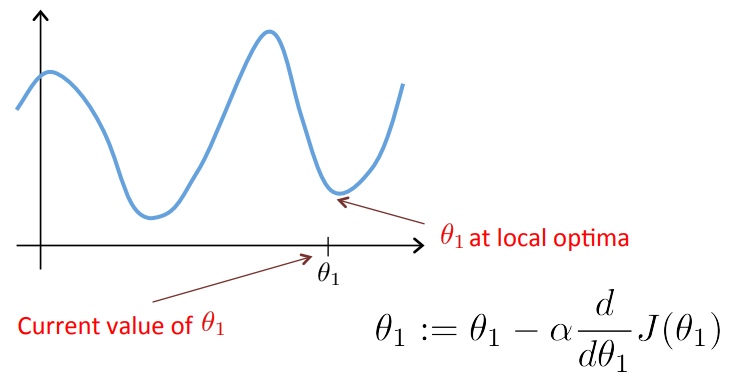
  • 이때의 미분계수는 0
  • 따라서 θ_1 := θ_1 - α * 0 이므로, θ_1의 값은 유지된다.

=> Gradient descent는 파라미터에 아무런 영향을 끼치지 않는다.

• α가 고정된 경우에도 gradient descent는 지역 최솟값에 수렴한다.
  • 최솟값에 가까워질수록 gradient descent는 자동 조정됨
    최솟값에 가까워질수록 미분계수 0에 가까워지고 있다는 것이기 때문

=> α값을 작게 조정해주지 않아도 된다.

Gradient Descent For Linear Regression

• 선형 회귀에 gradient descent를 적용하면 아래와 같은 식이 된다.
  
  
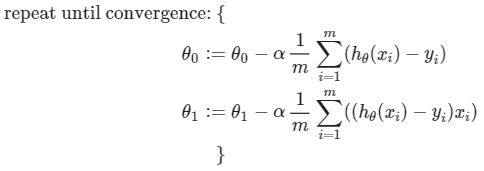
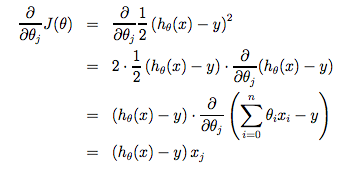
  • 훈련세트 전체를 사용하며 이를 "Batch" Gradient Descent 라고도 한다.
• 선형 회귀의 비용함수는 항상 convex function (볼록 함수)
  • 따라서 지역 최적값은 없고 항상 전역 최적값만 존재한다.
  • 즉, gradient descent는 항상 전역 최솟값에 수렴한다.

---

Linear Algebra Review

• 벡터 곱을 통해 크기가 큰 데이터에 대해서도 효율적인 계산을 할 수 있다.