Machine Learning by professor Andrew Ng in Coursera

Multivariate Linear Regression

다변량 선형 회귀

feature가 여러 개

Multiple Features

• 앞으로 사용할 표기법

  • n : feature 개수
  • m : training examples 개수
  • $x^i$ : i번째 training example
  • $x^i_j$ : i번째 training example에서 j번째 feature의 값

• $h_θ(x)$ = $θ_0$ + $θ_1*x_1$ + $θ_2*x_2$ + ... + $θ_n*x_n$

  • 벡터로 표현하면 $h_θ(x)$ = $θ^Tx$

Gradient Descent For Multiple Variables

• Hypothesis : $h_θ(x)$ = $θ^Tx$

• Parameters : $θ_0, θ_1, θ_2.. θ_n$ (n차원 벡터, nx1)

• 

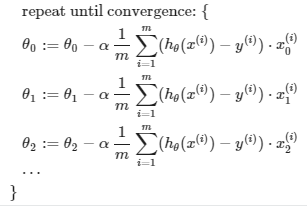
• 즉,

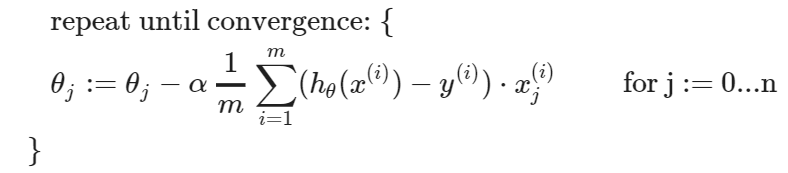
Gradient Descent in Practice I - Feature Scaling

• feature scaling
  : 다양한 단위를 갖는 변수들을 비교 가능한 단위로 바꿔준다.

• feature들의 scale이 같다면 gradient descent는 더 빨리 수렴한다.

• $-1 <= x_{(i)}<= 1$ 또는 $-0.5 <= x_{(i)}<= 0.5$ 가 적당하다.

• 정규화 (Normalization) - MinMaxScaler

  $x_{scaled}$ = $x - x_{min}\over x_{max}-x_{min}$

  • 데이터에서 최솟값을 뺀 후 최댓값과 최솟값의 차이로 나눈다.
  • 0~1 범위에 들도록 값을 이동하고 스케일을 조정한다.
  • 0~1을 원하지 않는다면 범위를 변경할 수 있다.

• 표준화 (Standardization) - StandardScaler

  $x_{scaled}$ = $x - μ\over σ$

  • 평균을 뺸 후 표준편차로 나누어 결과 분포의 분산이 1이 되도록 한다.
  • 평균이 0, 분산이 1인 가우시안 정규 분포를 가진 값으로 변환

SVM, 선형회귀, 로지스틱회귀 모델은 데이터가 가우시안 분포를 따른다고 가정하기 때문에 사전에 학습 데이터에 표준화를 적용하는 것이 모델의 예측 성능 향상에 도움이 된다.

• Mean Normalization

  $x_{scaled}$ = $x - μ\over x_{max} - x_{min}$

  • 전체 평균을 대략 0으로 만든다.

Gradient Descent in Practice II - Learning Rate

• gradient descent가 잘 동작하고 있다면 J(θ)는 반드시 감소해야 한다.
  
• α를 여러 값으로 바꿔가며 그래프를 그려보고 가장 빠르게 수렴하는 α를 선택한다.
  -> 이렇게 gradient descent를 구현한다.
• learning rate가 너무 크면 최솟값을 지나칠 수 있다.
  
• learning rate 값이 너무 작으면 : 천천히 수렴
• learning rate 값이 너무 크면 : 반복마다 J(θ)가 감소하지 않고 따라서 수렴하지 않는다.

Features and Polynomial Regression

• 예를들어 Housing Price Prediction에서
  • frontage 와 depth 특성이 주어졌을 때 이 두 특성의 값들을 곱해서 area라는 새로운 특성을 내가 추가할 수 있다.

Polynomial Regression

• 아래와 같은 데이터가 주어졌을 때
  

  • $h_θ(x) = θ_0 + θ_1x_1$ (직선) 은 데이터를 잘 표현하지 못한다.

    • 주어진 특성 $x_1$을 이용해서 새로운 특성들을 추가해 본다.
      -> 모델1 : $h_θ(x) = θ_0 + θ_1x_1 + θ_2x_1^2$
      -> 모델2 : $h_θ(x) = θ_0 + θ_1x_1 + θ_2x_1^2 + θ_3x_1^3$

      • 모델2 에서 $x_2 = x_1^2$ , $x_3 = x_1^3$ 로 설정하고 선형회귀 형태를 적용하면
        -> $h_θ(x) = θ_0 + θ_1x_1 + θ_2x_2 + θ_3x_3$

    • 다른 방법
      -> $h_θ(x) = θ_0 + θ_1x_1 + θ_2\sqrt{x_1}$
      모델1을 선택하지 않았던 건 이차함수 즉, 볼록함수는 값이 점점 줄어들기 때문이었다. 루트 값을 더해주면 값이 크게 증가하지는 않지만 줄어들지는 않는다.

    => 특성을 이런식으로 선택했다면 feature scaling이 매우 중요하다.
    그래야 gradient descent를 할 때 비슷한 범위를 갖는다.
    

feature를 선택하는 여러 방법이 있다.
새로운 특성을 추가해서 더 복잡한 함수로 데이터를 잘 표현하도록 할 수 있다.

---

Computing Parameters Analytically

Normal Equation

• 특정 선형 회귀 문제에서 파라미터 θ의 최적값을 효과적으로 구하는 방법

• 아래의 공식을 통해 알고리즘의 반복 없이 한 번에 비용함수를 최소화하는 θ값을 구한다.

  $θ$ = $(X^TX)^{-1}X^Ty$

  • θ : n+1 차원 벡터
    모든 샘플에 대해 값이 모두 1인 $x_0$ 를 추가해주기 때문에 n+1
  • X : m x (n+1) 행렬
  • y : (m x 1) 벡터

• 이때 feature scaling은 불필요하다.

• Gradient Descent vs Normal Equation
  m개의 샘플 & n개의 특성

  Gradient Descent	Normal Equation
  α 선택 필요	α 선택 불필요
  iterations o	iteration x
  O(k$n^2$)	O($n^3$) ($X^TX$를 계산)
  n이 클 때 적합 (역행렬 구하는 시간보다는 적게 걸린다.)	n이 크면 속도가 느려짐

  보통 n x n 크기 행렬의 역행렬을 구하는 시간 = $O(n^3)$

=> n이 작으면 normal equation, n이 크다면 gradient descent

Normal Equation Noninvertibility

만약 $(X^TX)$ 의 역행렬이 존재하지 않는다면?

• redundant features 확인
  • 예를 들어 $x_2$ 특성이 곧 $x_1^2$이라면 둘 중 하나는 지운다.
• feature가 많은 경우, (m 샘플수 < n 특성수) 인지 확인
  • 특성 몇 개를 삭제 또는 regulation(규제) 적용

하지만 역행렬이 없는 경우는 드물다.