[ML] 3주차-4 : underfitting, overfitting, regularization

Machine Learning by professor Andrew Ng in Coursera

1) The Problem of Overfitting

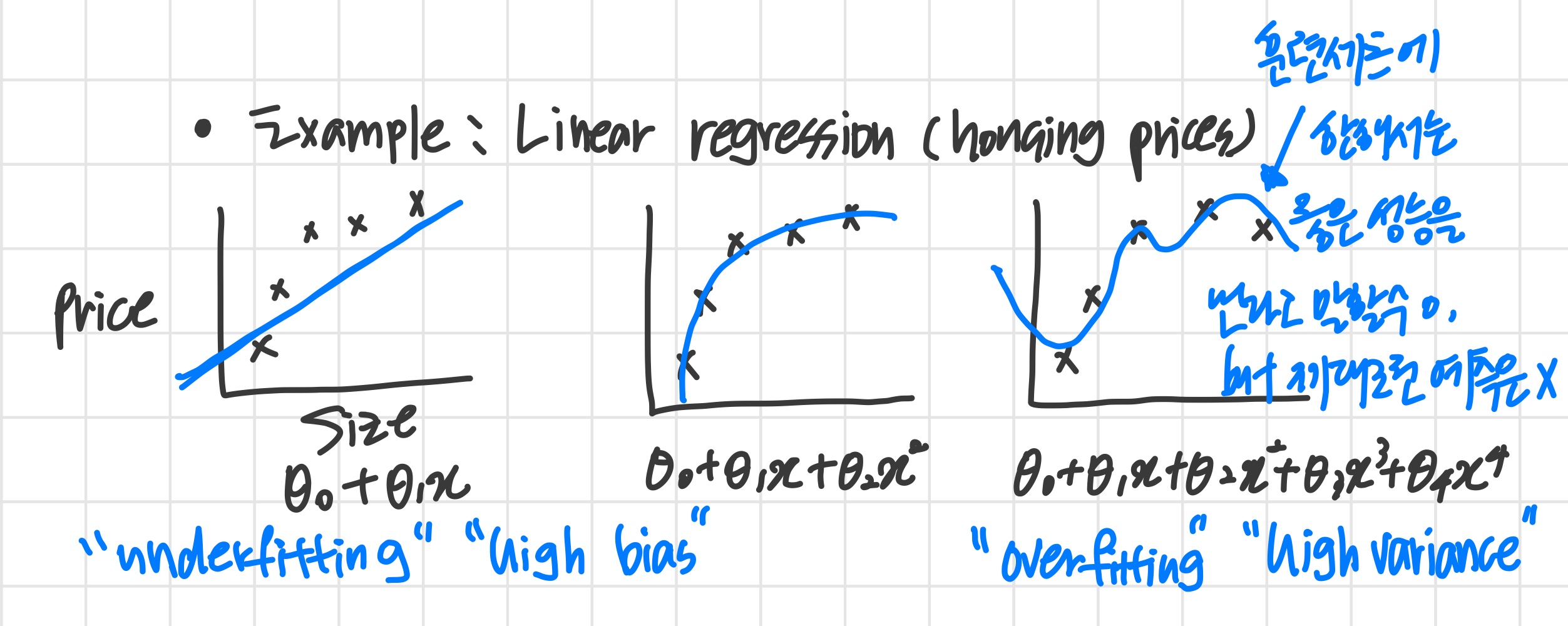
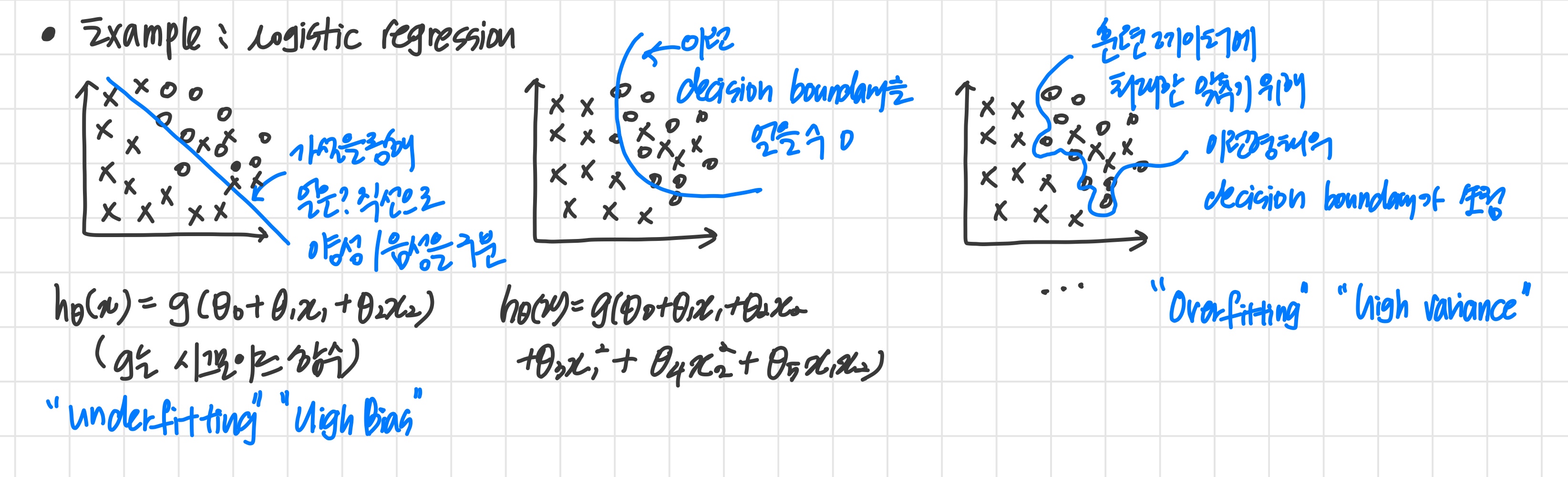
• Overfitting
  : feature가 많으면 hypothesis function은 training set 에 맞추려 하기 때문에 매우 복잡해진다.
  (위의 그림에서 굴곡이 많은 세번째 파란색 그래프처럼 )
  주어진 training set와는 데이터 분포가 거의 일치하는데 정작 새로운 데이터에 대한 예측을 잘 해내지 못하게 된다.

Adressing overfitting

---

overfitting 해결방법

1. Reduce number of features

• 사용할 feature와 사용하지 않을 feature를 구분한다.
• Model selection algorithm (이후 강의에서 배운다)

단점 : 몇몇 feature를 버리면서 주어진 문제의 정보를 같이 잃게 된다.

2. Regularization

• 모든 feature를 유지하되, parameter $\theta_j$의 영향 규모를 줄인다.
  즉, $\theta$값이 미치는 영향을 줄인다.
• 많은 feature가 $y$를 예측하는 데에 조금씩 기여하는 경우 유용하다.

underfitting / high bias
hypothesis function이 training set를 잘 나타내지 못하거나
feature의 개수가 너무 적거나
hypothesis function이 너무 단순할 때
overfitting / high variance
training set와는 일치하지만 새로운 데이터에 대한 예측은 잘 못하거나
hypothesis function이 너무 복잡할 때 (curve와 angle이 많다)

2) Cost function

Regularization

---

parameters $\theta_0, \theta_1, \theta_2 ..$ 들이 작은 값을 갖도록 하면

• hypothesis가 더 단순해진다.
• overfitting 가능성이 줄어든다.

예제) Housing

• Features : $x_1, x_2, ...$
• Parameters : $\theta_0, \theta_1, ...$

feature가 많아서 어떤 feature의 영향을 줄일지 선택하는 게 어렵다.
이때 linear regression의 cost function을 이용하는데 regularization term이 추가된다.

$J(\theta) = \frac{1}{2m} \left[\sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2\color{royalblue}{+\lambda\sum_{j=1}^{n}\theta_j^2}\right]$

regularized linear regression에서 위의 $J(\theta)$을 최소화하는 세타를 구한다.

$\lambda$ 를 통해 parameter의 크기를 작게 유지할 수 있다.

만약 $\lambda$가 매우 큰 값을 가진다면?

$\lambda$값이 커지면 $J(\theta)$값을 최소화하기 위해 $\theta_0, \theta_1, \theta_n...$은 모두 0에 가까운 값이 된다.
그럼 결국 underfitting 문제가 발생하게 된다.

즉, regularization 방법을 쓴다면 적절한 $\lambda$값 설정이 중요하다.

3) Regularized Linear Regression

Regularized Linear Regression

---

$J(\theta) = \frac{1}{2m} \left[\sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2\color{royalblue}{+\lambda\sum_{j=1}^{n}\theta_j^2}\right]$
$\min_\theta J(\theta)$

Linear regression의 최적의 parameter는 찾는 방법
: gradient descent와 normal equation

Gradient Descent

---

Normal Equation

---

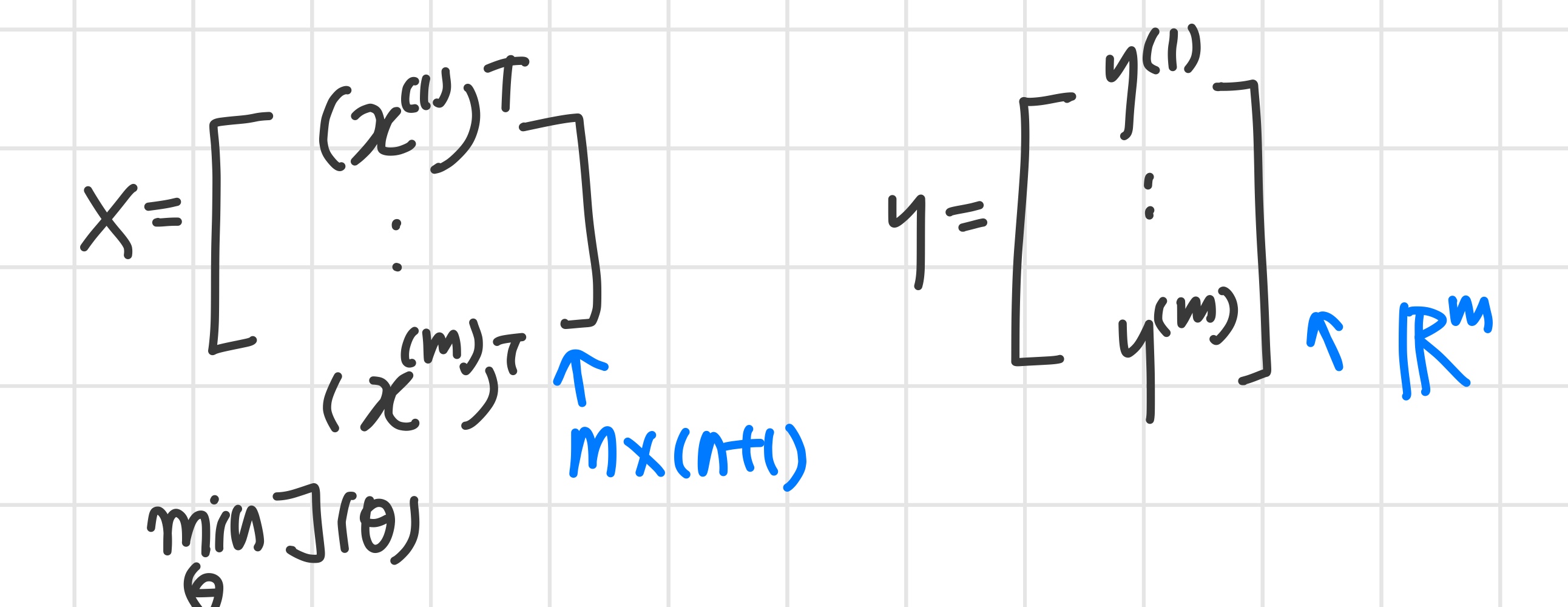
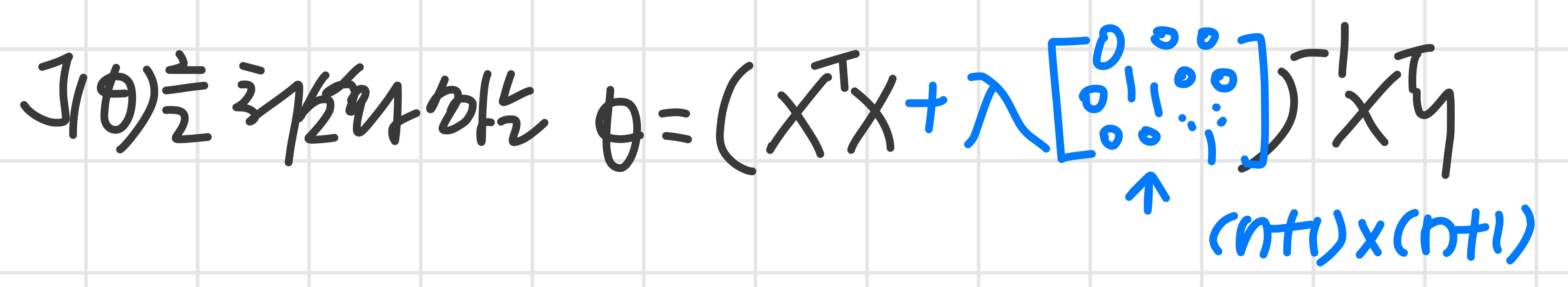
training set가 상대적으로 작고 feature는 많더라도 regularized term 을 추가한 것에 대한 gradient descent와 normal equation을 통해 overfitting을 막을 수 있다.

4) Regularized Logistic Regression

Regularized Logistic Regression

---

logistic regression에도 regularization을 적용해 본다.

$J(\theta) = -\{\frac{1}{m} \sum_{i=1}^{m}y^{(i)}\log h_\theta(x^{(i)}) + (1 - y^{(i)}) log(1 - h_\theta(x^{(i)}))\} + \frac{\lambda}{2m}\sum_{j=1}^{n}\theta_j^2$

feature가 많더라도 regularization을 통해 parameter값들을 작게 유지할 수 있다.

Gradient Descent

---