Machine Learning by professor Andrew Ng in Coursera
0) Non-linear Hypotheses
linear regression과 logistic regression이 있는데 neural network를 왜 더 배워야 할까
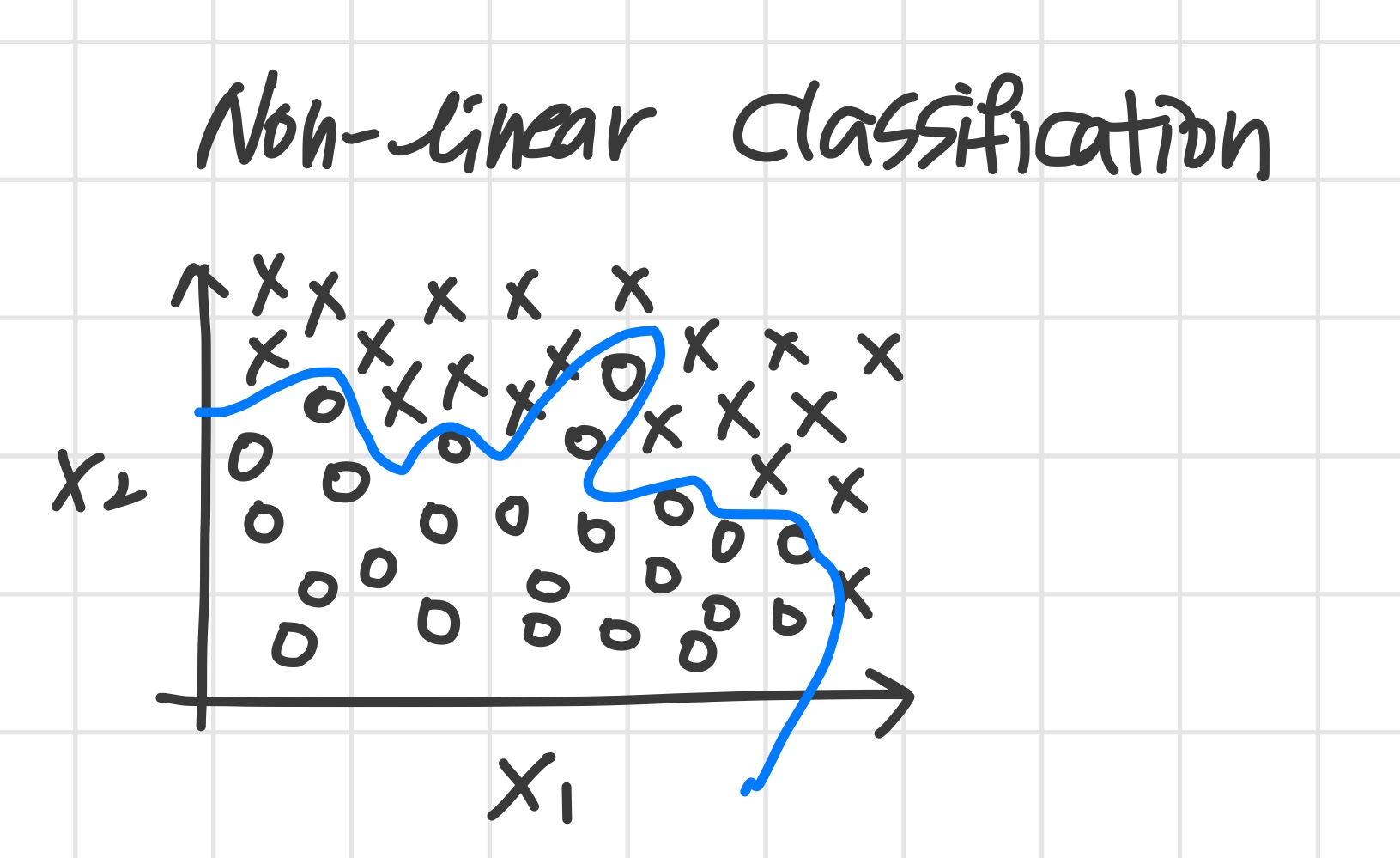
위의 그림과 같이 logistic regression을 통해 non-linear boundary를 만드는 것이 가능하다.
하지만 위의 상황은 feature가 2개뿐이었기에 가능했다.
대부분의 머신러닝 문제들은 feature가 매우 많다.
원래 feature 개수가 많았다면 위의 방법을 적용하면 그 개수가 엄청나게 늘어나게 된다.
또한 연산량도 증가하고 overfitting 가능성도 높아진다.
1) Model Representation I
Neuron model: Logistic unit
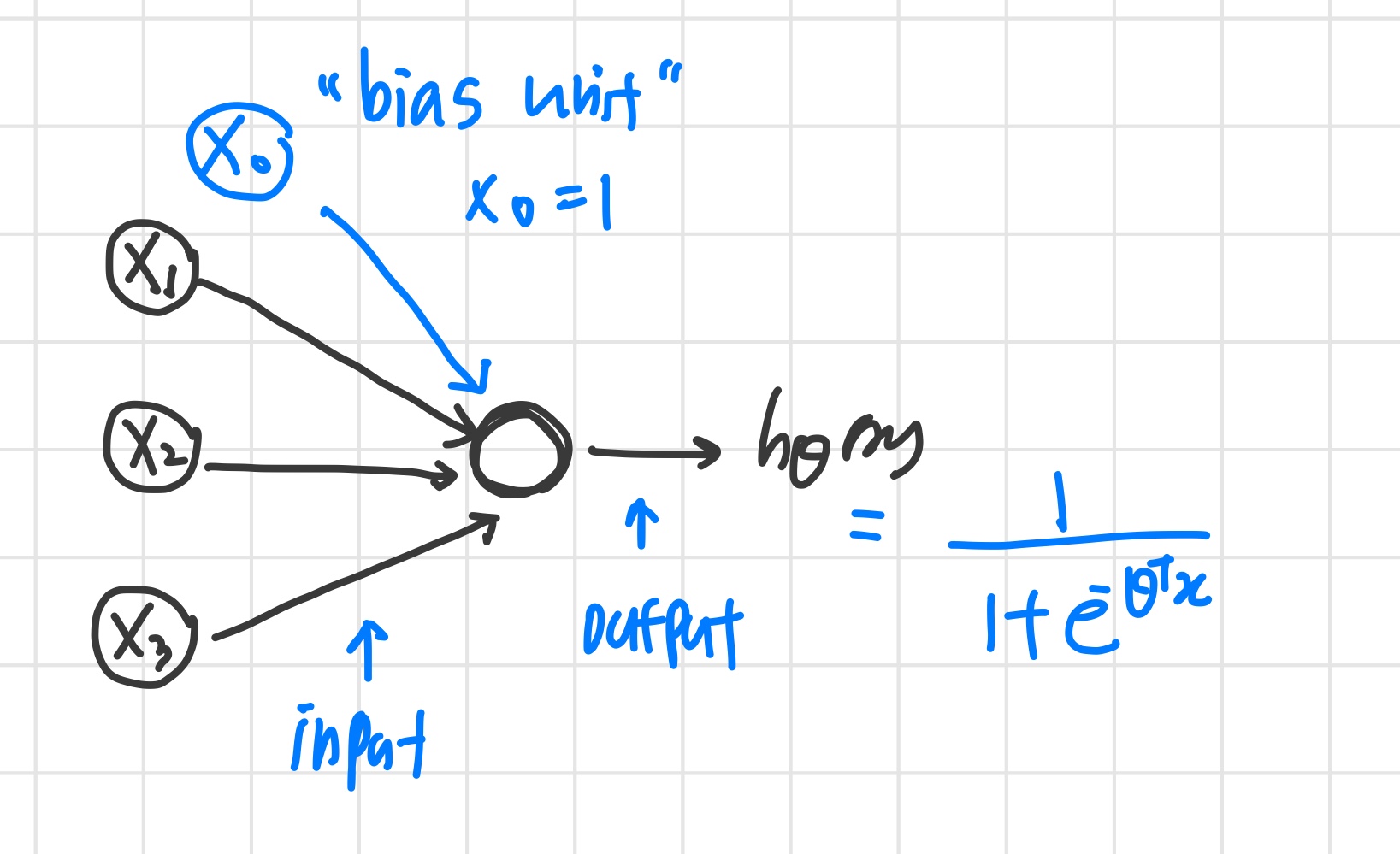
- 는 bias unit으로 항상 1의 값을 가지며 굳이 나타내지 않기도 한다.
- 는 logistic function을 사용하는데, sigmoid activation function (non-linearity g(z)) 이라 부르기도 한다.
- 들을 weight 라고 부른다.
이제 여러 개의 뉴런을 살펴보자.
Neural Network
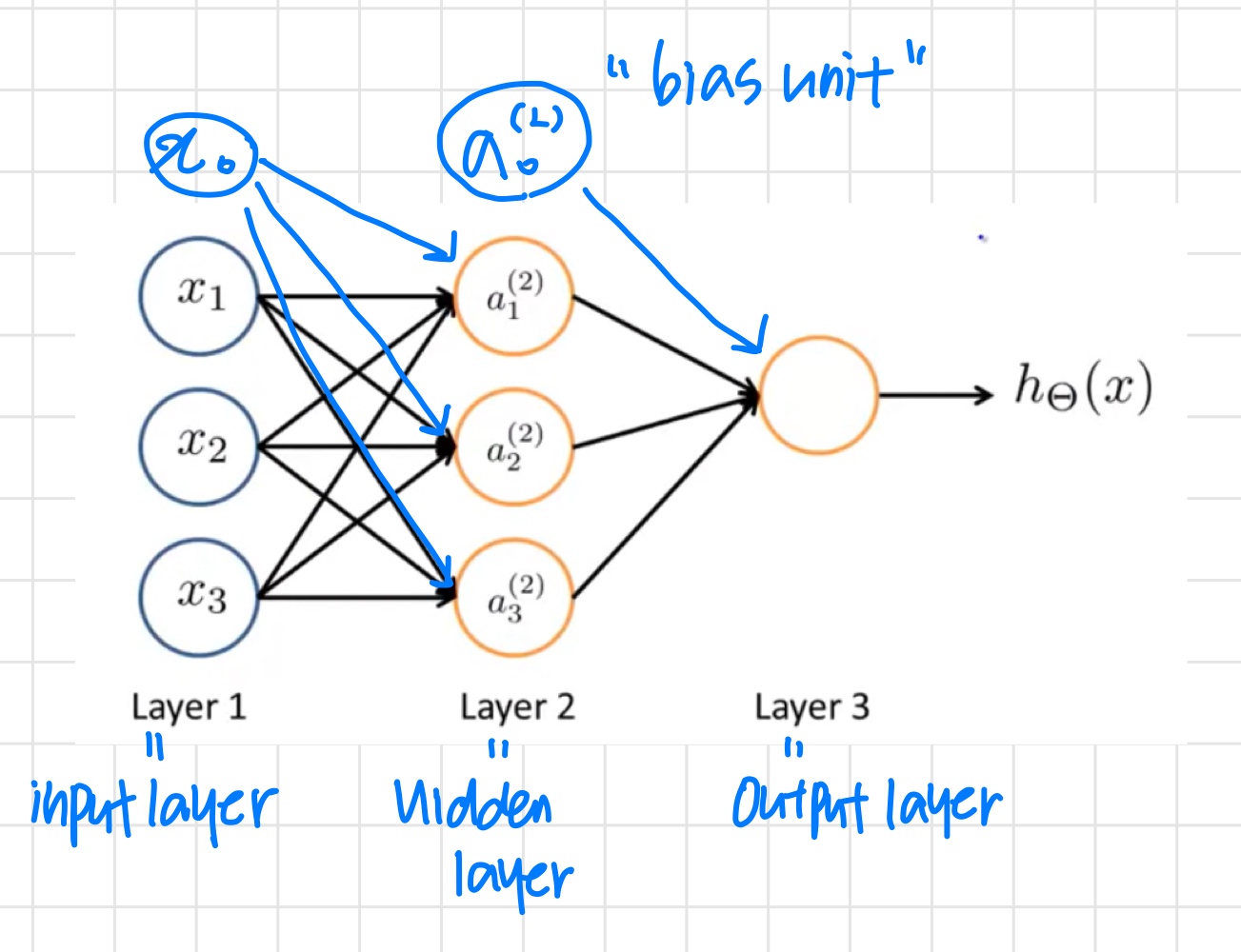
- 첫 번째 layer : input layer
- 마지막 layer : output layer
- input과 output의 중간 layer들 : hidden layer
- 이때 hidden layer의 node들을 (unit in layer )로 나타내고 activation unit 이라고 부른다.
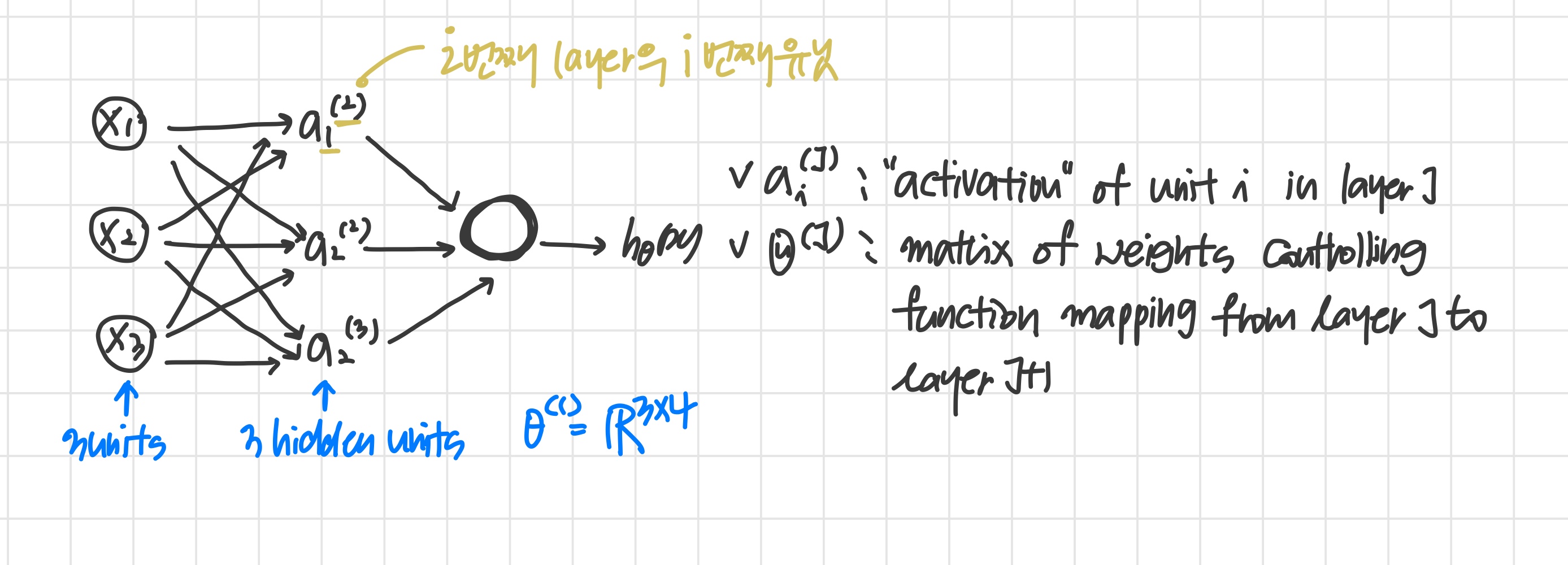
이때 각 activation node의 계산은 다음과 같다.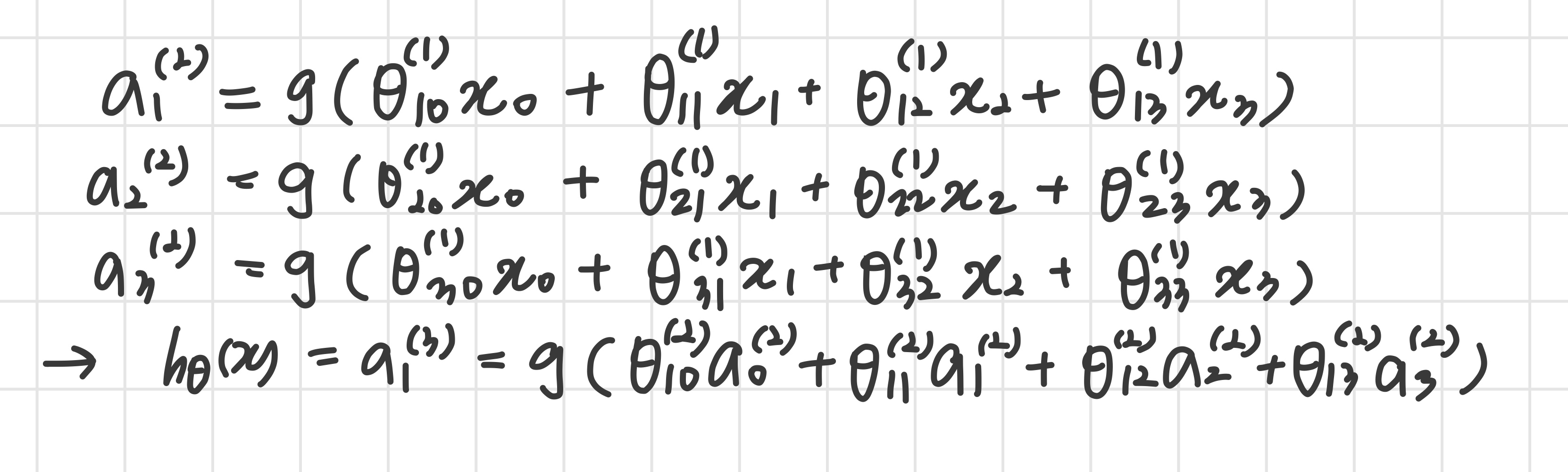
각 layer는 고유한 weight matrix 를 갖는다.
만약 network가 layer 에 개 unit을 갖고, layer 에 개의 unit을 갖는다면 의 dimension은
2) Model Representation II
Forward propagation: Vectorized implementation
앞의 함수들을 새로운 변수 를 이용하여 vector로 표현해 본다.
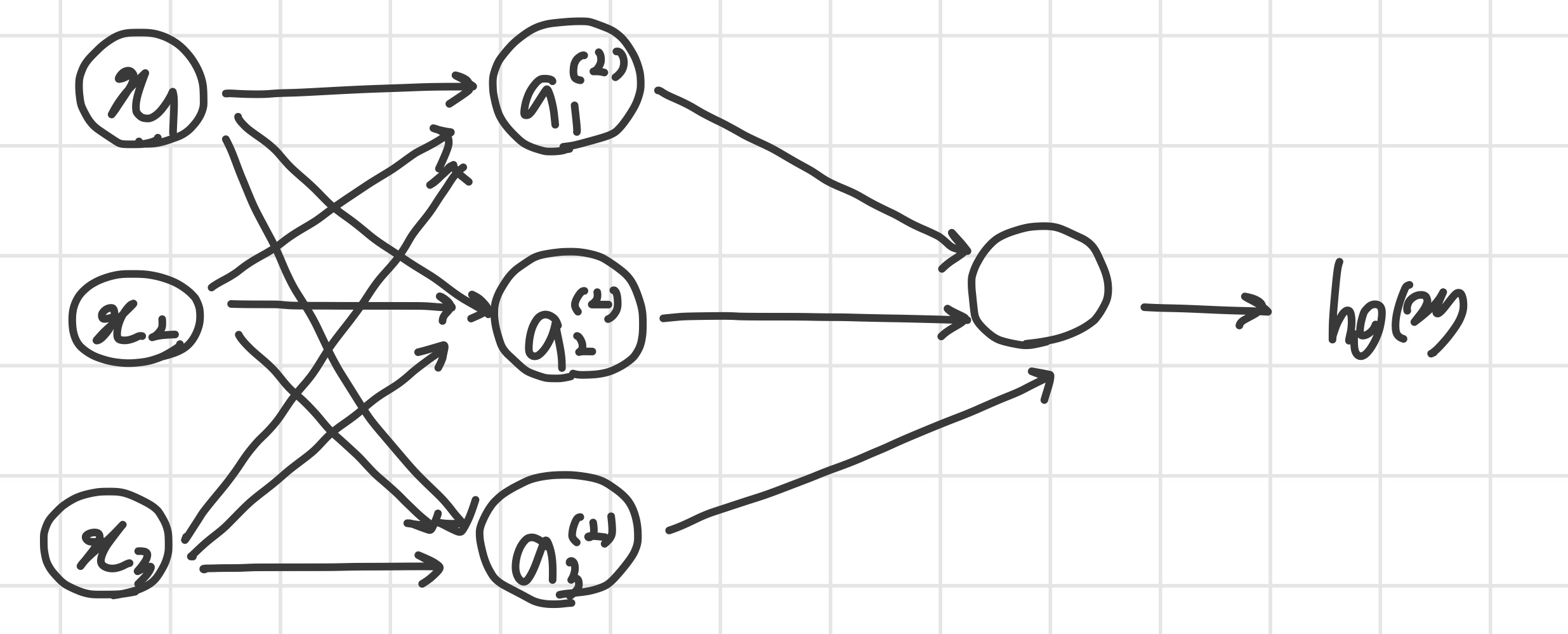
즉, layer , node 에 대해 변수는 다음과 같다.
와 를 벡터로 나타내면
라 할때 식을 일반화하면,
최종 vector는 다음 행렬과 모든 activation node에서의 값의 곱으로 구한다. 최종 theta matrix 는 단 하나의 행을 가지므로, 그 결과는 single number가 된다. 최종결과는 다음과 같다.
마지막 단계에서 layer 와 사이에서, logistic regression에서 했던 것과 정확히 같은 방식이 쓰이는 점을 주목하자.
이렇게 중간 layer 들을 쌓아 올림으로써 더욱 복잡한 non-linear hypothesis를 생성해낼 수 있다.
Neural Network Learning its Own Features
logistic regression과 다른 점은 주어진 feature를 그대로 쓰지 않고 를 쓴다는 점
