[ML] 6주차-2 : Bias vs. Variance

Machine Learning by professor Andrew Ng in Coursera

1) Diagnosing Bias vs. Variance

Bias vs. Variance

---

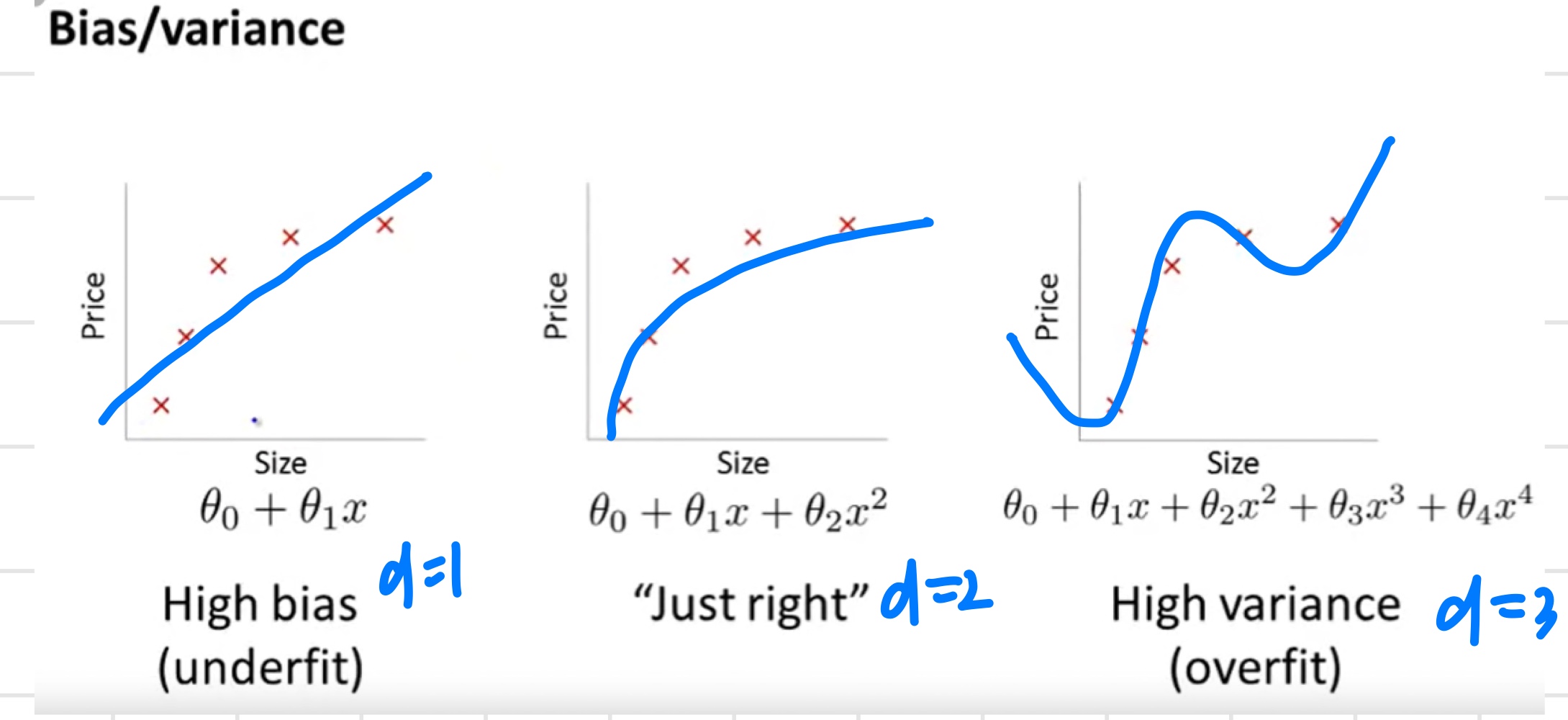
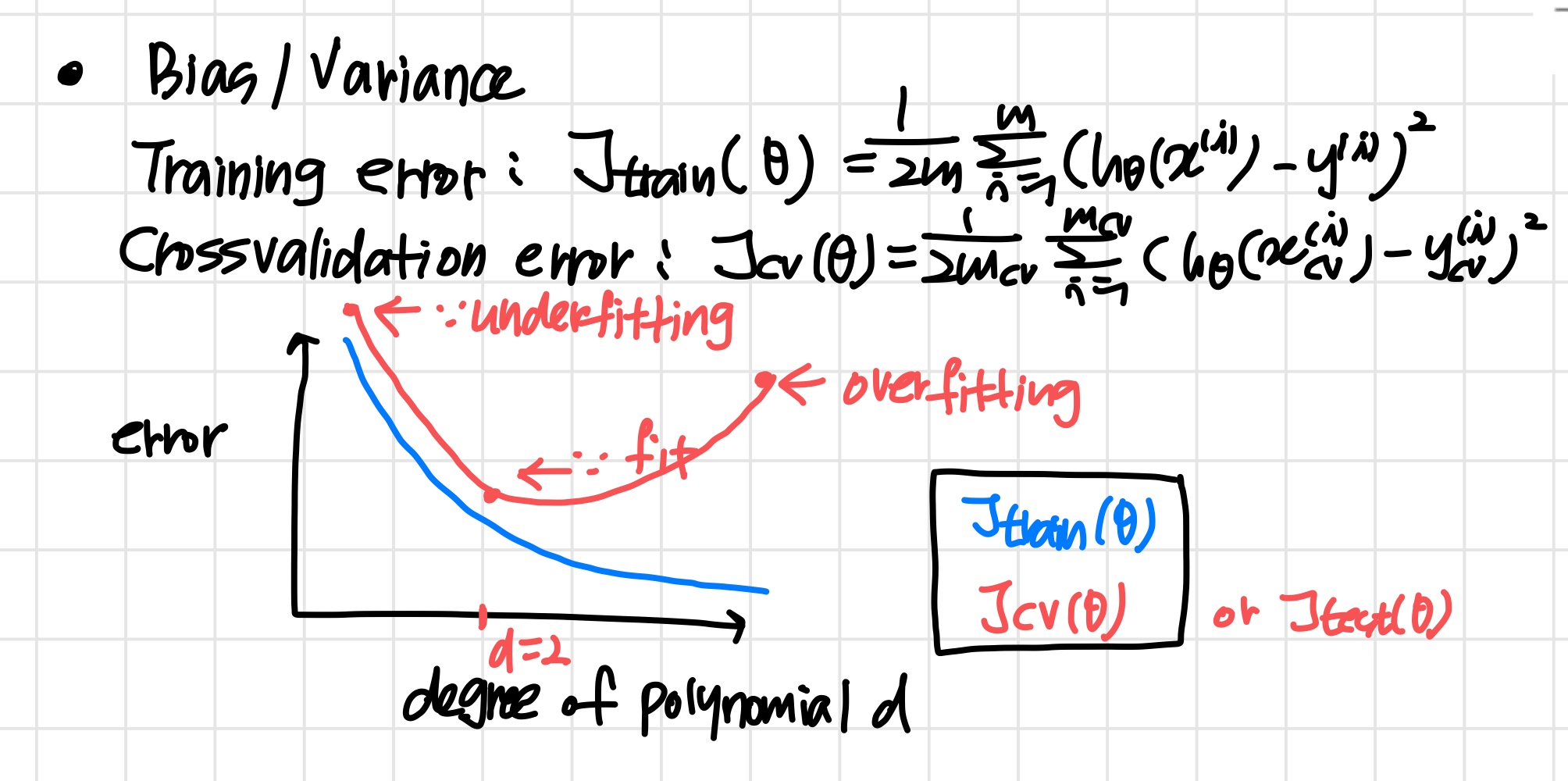
Diagnosing bias vs. variance

---

learning algorithm의 성능이 좋지 않다면 (즉, $J_{cv}(\theta) \text{ or } J_{test}(\theta)$값이 크다면)
bias 문제일까 variance 문제일까

• High bias (underfitting) :
  $J_{train}(\theta)$와 $J_{CV}(\theta)$ 모두 값이 크다. 또한 $J_{train}(\theta) \approx J_{CV}(\theta)$
• High variance (overfitting) :
  $J_{train}(\theta)$ 값은 작고 $J_{CV}(\theta)$ 값은 $J_{train}(\theta)$ 보다 훨씬 크다.

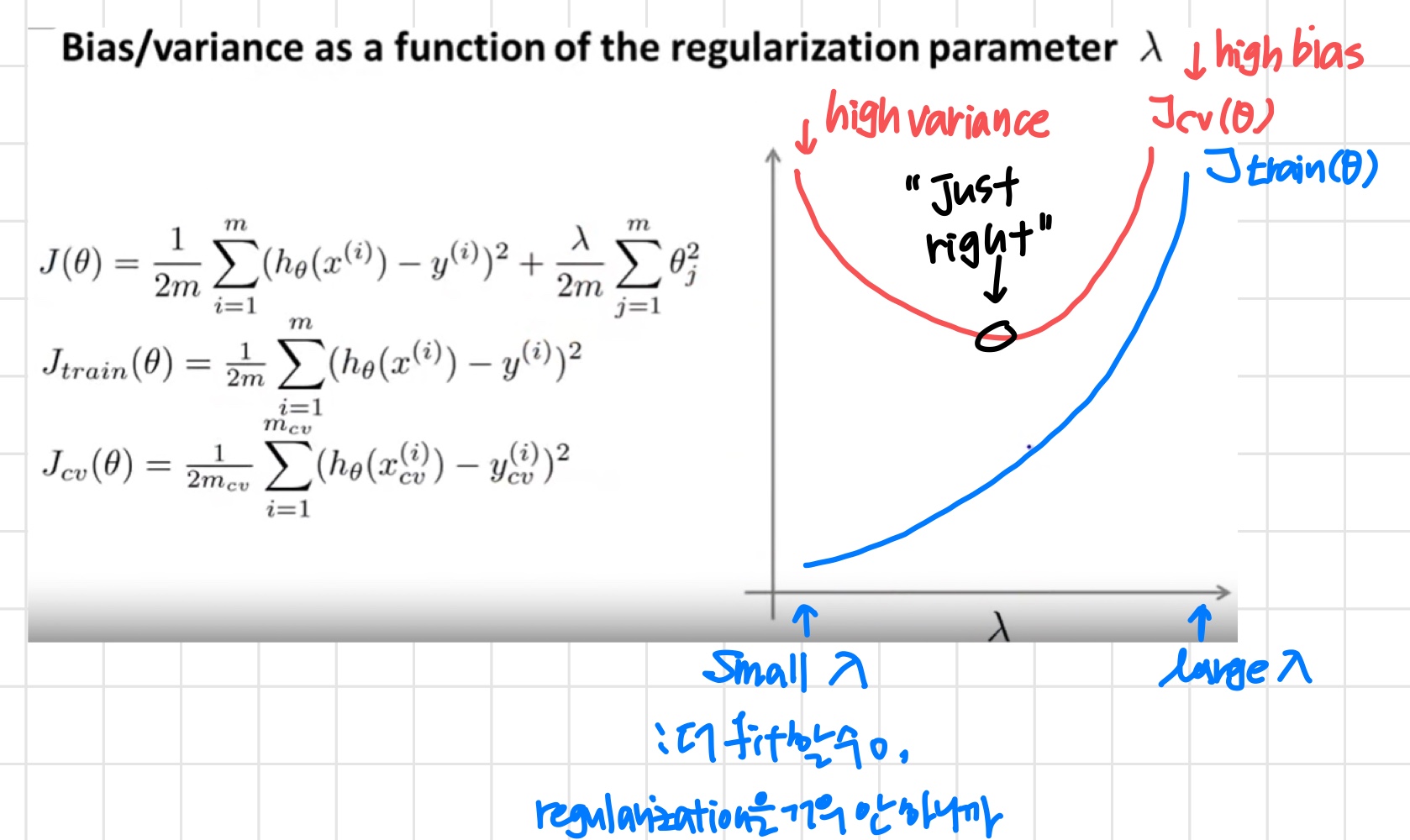
2) Regularization and Bias/Variance

Linear regression with regularization

---

'이때 $h_\theta(x)$ 가 high polynomial이기 때문에 overfitting을 막기 위해 regularization term을 추가한 것. 이를 통해 파라미터 값들을 작게 유지할 수 있다.'

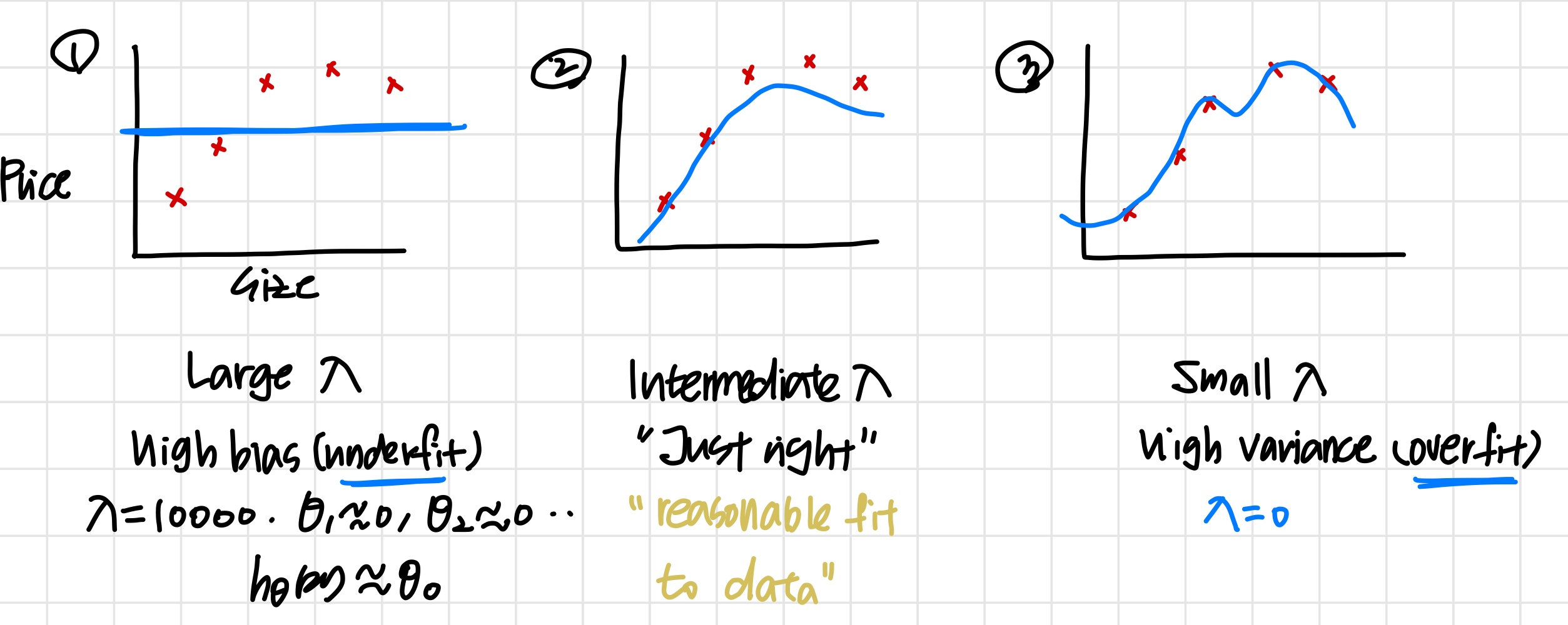
'적절한 λ를 어떻게 고를까?'

Choosing the regularization parameter $\lambda$

---

우선 $J_{train}(\theta), J_{cv}(\theta), J_{test}(\theta)$를 아래와 같이 정의한다.
이때 regularization term을 포함하지 않는다.

1. Create a list of lambdas (i.e. λ∈{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24});
2. Create a set of models with different degrees or any other variants.
3. Iterate through the λs and for each λ go through all the models to learn some Θ.
4. Compute the cross validation error using the learned Θ (computed with λ) on the $J_{CV}(\Theta)$ without regularization or λ = 0.
5. Select the best combo that produces the lowest error on the cross validation set.
6. Using the best combo Θ and λ, apply it on $J_{test}(\Theta)$ to see if it has a good generalization of the problem.

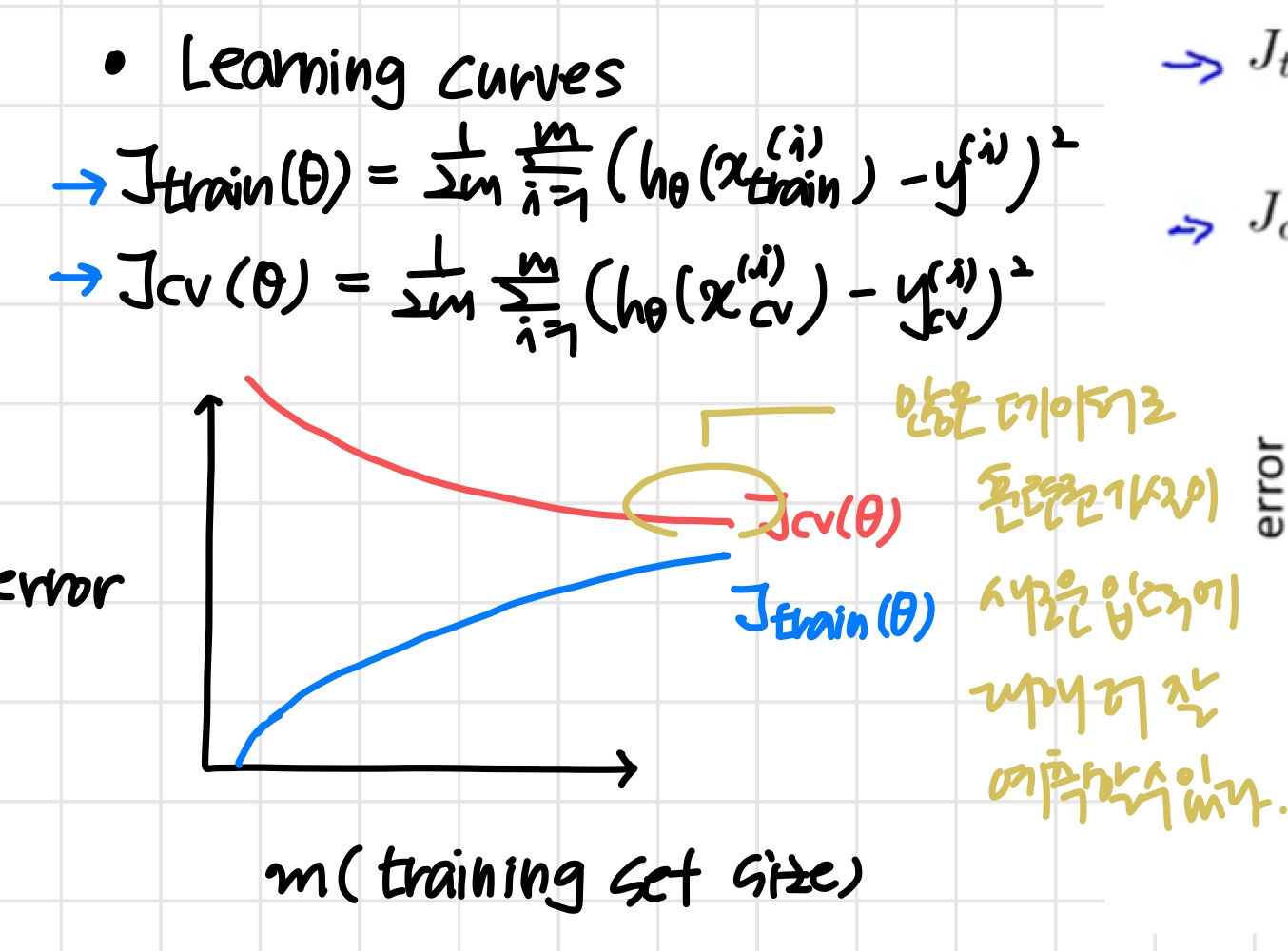
3) Learning Curves

training set 크기에 따른 error를 나타낸 그래프
'만약 training set가 1개뿐 이라면 완벽하게 fit할 수 있다.'

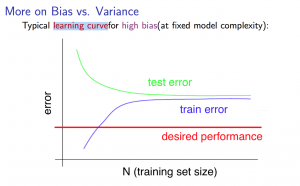
High bias

---

'인 알고리즘의 학습 곡선'

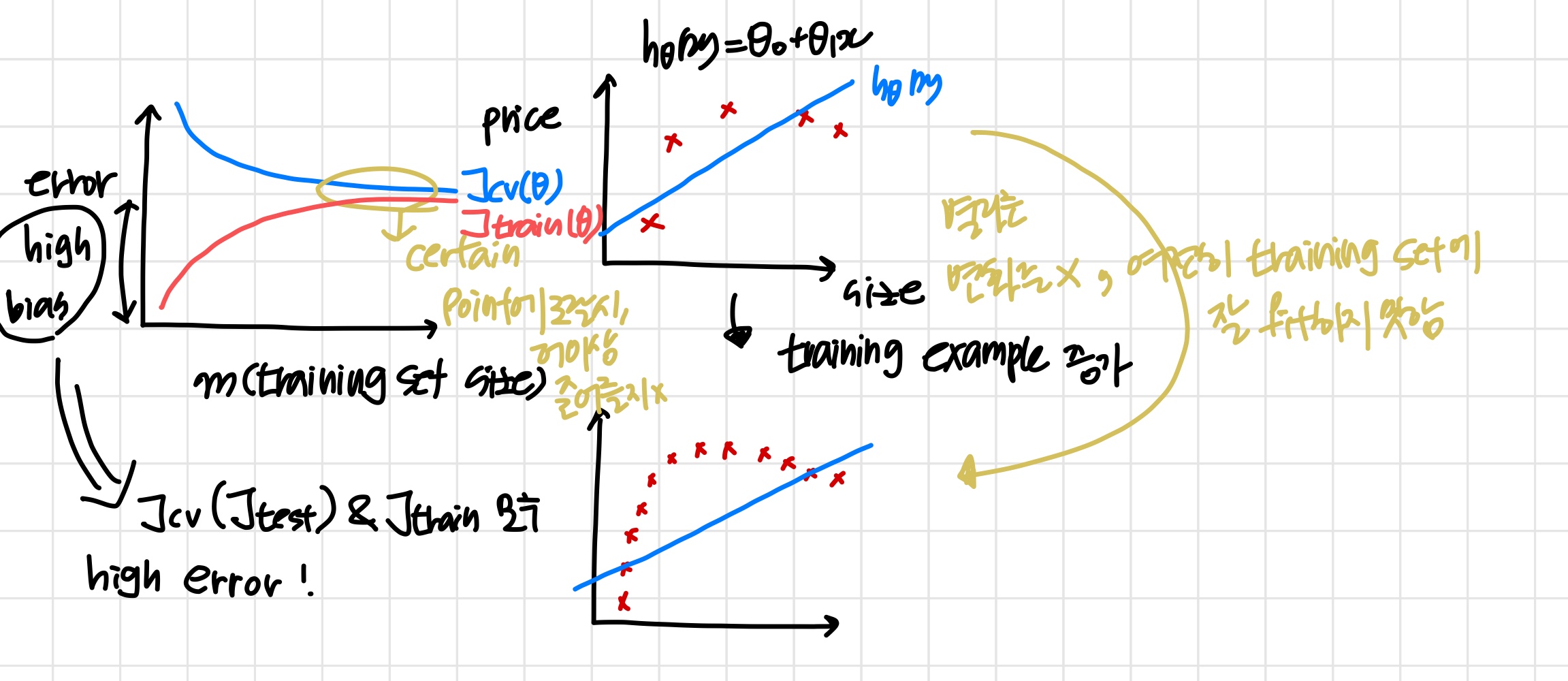
• Low training set size : $J_{train}(\theta)$은 작아지고 $J_{CV}(\theta)$는 커진다.
• Large training set size : $J_{train}(\theta)$과 $J_{CV}(\theta)$ 모두 커지며 이때 $J_{train}(\theta) \approx J_{CV}(\theta)$.
• 만약 high bias라면 training set 크기가 커지는 것은 별다른 도움이 되지 않는다.

High variance

---

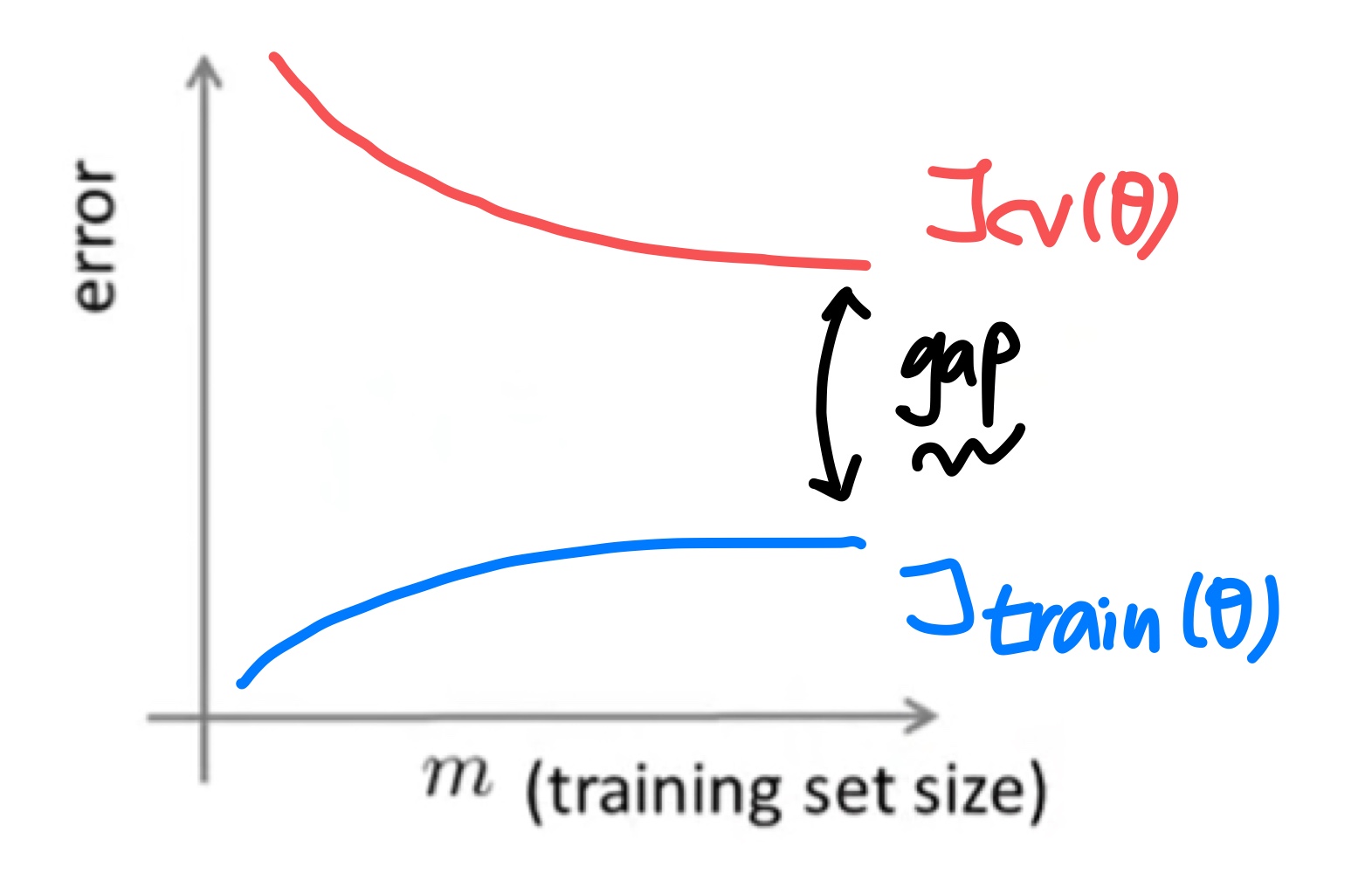
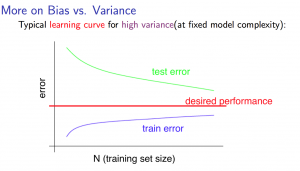
• Low training set size : $J_{train}(\theta)$은 작아지고 $J_{CV}(\theta)$는 커진다.
• Large training set size : training set size가 증가함에 따라 $J_{train}(\theta)$도 증가하고 $J_{CV}(\theta)$는 감소한다.
  Also, $J_{train}(\Theta) < J_{CV}(\Theta)$ but the difference between them remains significant.
• 만약 high variance라면 training set 크기가 커지는 것은 도움이 될 가능성이 높다.

4) Deciding What to do Next Revisited

만약 housing price를 예측하는 regularized linear regression을 만들었는데 새로운 데이터에 대한 예측을 계속해서 실패한다면 다음에 무엇을 해야할까

• 더 많은 training example을 구한다
  -> high variance를 고칠 수 있다.
• feature의 개수를 줄인다.
  -> high variance를 고칠 수 있다.
• feature의 개수를 늘린다.
  -> high bias를 고칠 수 있다.
• polynomial features를 추가한다.
  -> high bias를 고칠 수 있다.
• $\lambda$를 줄인다.
  -> high bias를 고칠 수 있다.
• $\lambda$를 늘린다.
  -> high variance를 고칠 수 있다.
  

'learning curve를 그려보고 현재 상태가 high bias/variance 인지 판단 후 위의 방법들 중 적절한 것을 선택한다.'

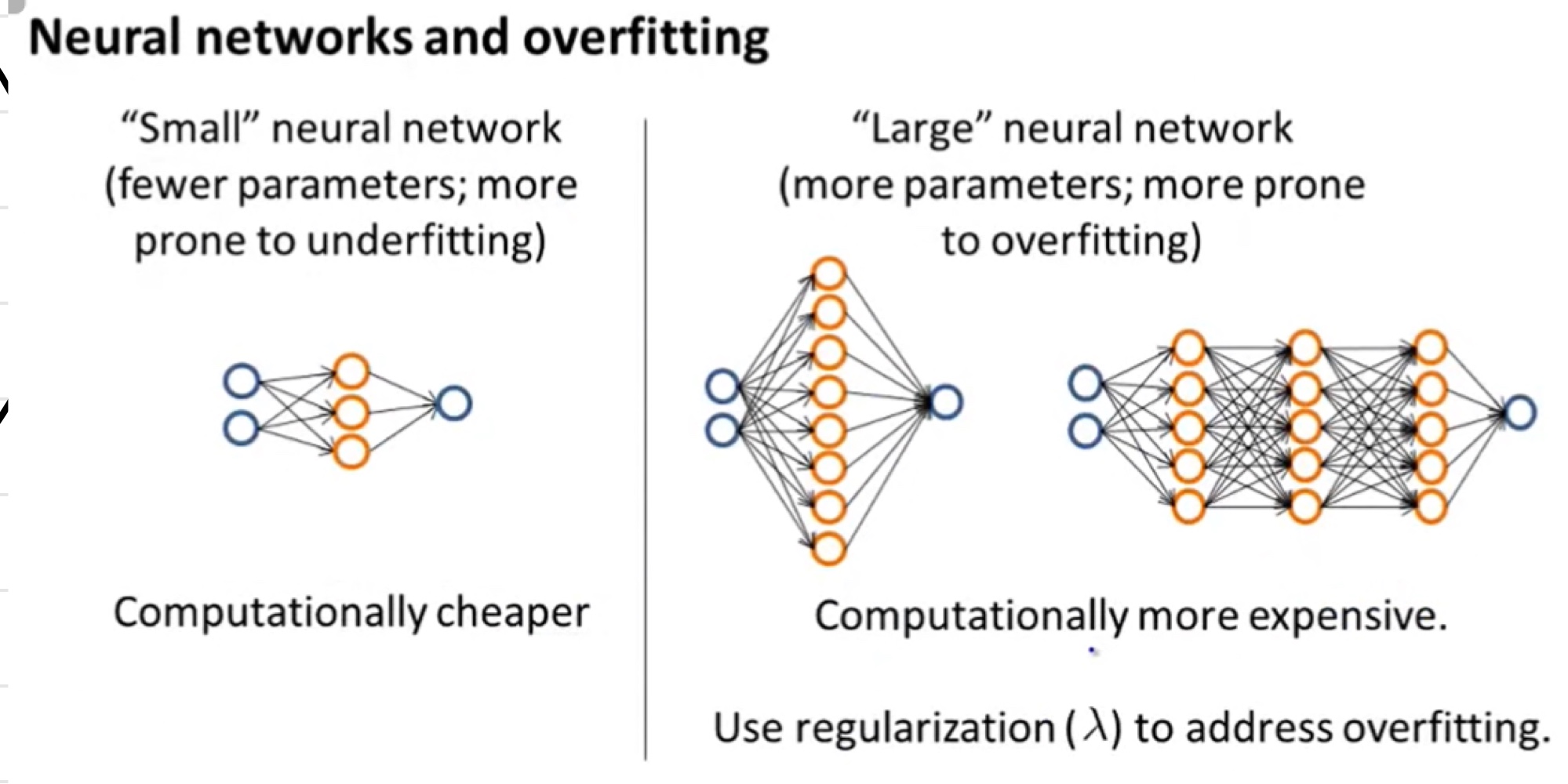
Neural Networks and Overfitting

---