[ML] 6주차-1 : Evaluating a Learning Algorithm

Machine Learning by professor Andrew Ng in Coursera

1) Deciding What to Try Next

Debugging a learning algorithm

---

housing price 예측을 위해 regularized linear regression을 실행했다고 가정한다.

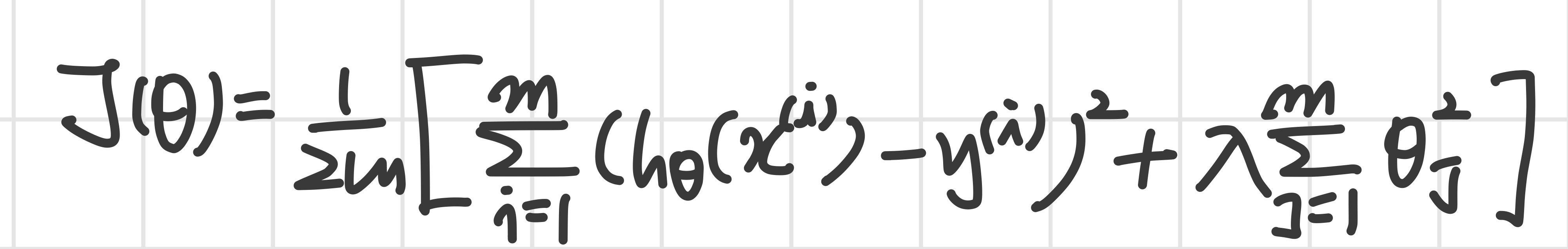
그러나 hypothesis를 새로운 데이터에 테스트해보니 예측에 에러가 많다.
어떻게 할까?

• Getting more training examples
• Trying smaller sets of features
• Trying additional features
• Trying polynomial features
• Increasing or decreasing λ

위의 방법들 중 적절한 것을 선택해야 한다.

Machine learning diagnostic:

---

Diagnostic: A test that you can run to gain insight what is/isn't working with a learning algorithm, and gain guidances as to how best to improve its performance.

Diagnostic은 시간이 걸리긴 하지만 이를 통해 이후의 시간을 효과적으로 사용할 수 있다.

2) Evaluating a Hypothesis

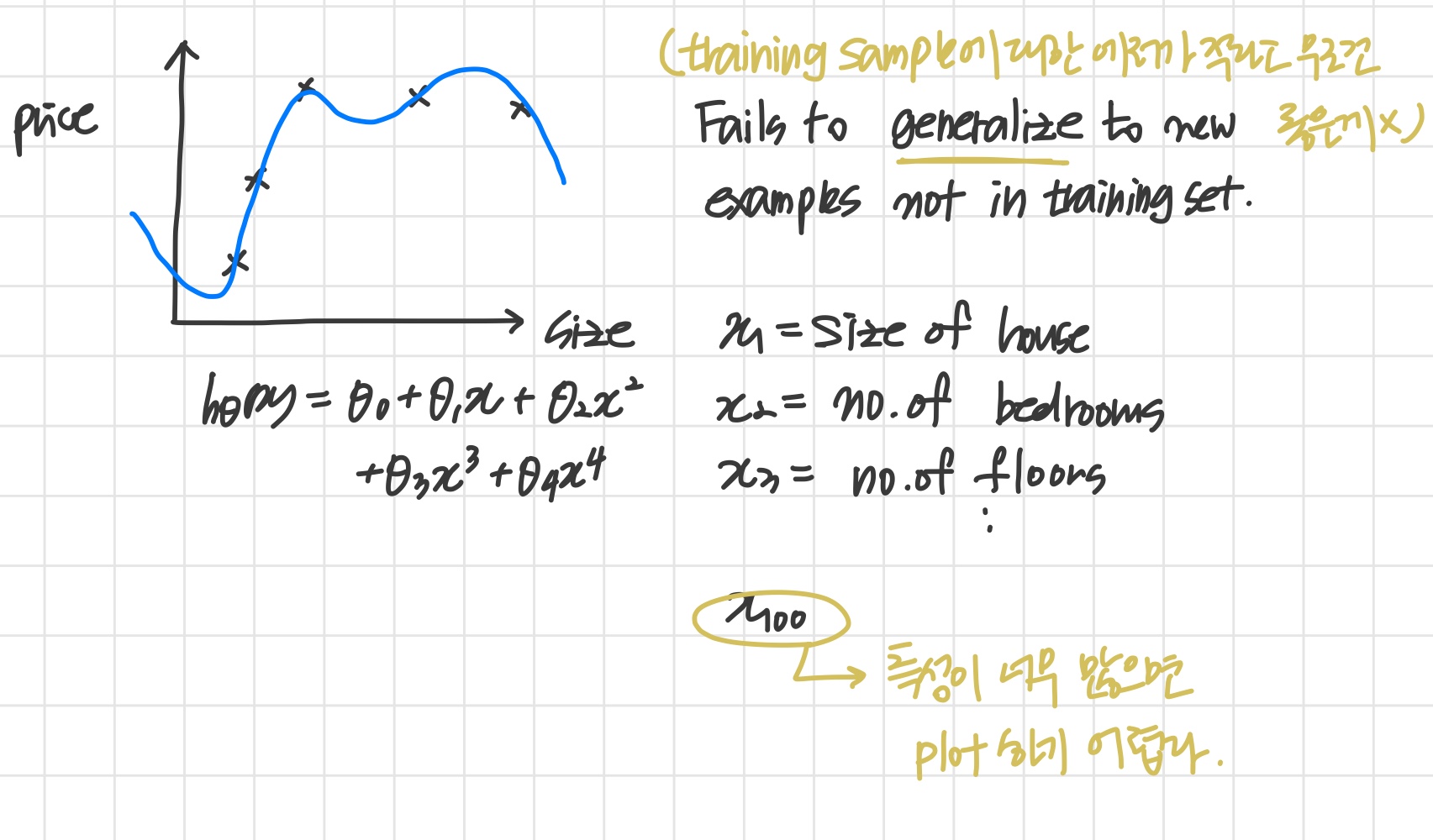
Evaluating hypothesis

---

training set를 training set + test set 로 나눈다.
이때 비율은 보통 training (70) + test (30)

Training/testing procedure for linear regression

---

1. $J_{train}(\Theta)$를 최소화하는 $\Theta$를 얻는다.
2. test set error 즉, $J_{test}(\Theta)$를 계산한다.

이때 test set error란

• For linear regression: $J_{test}(\theta) = \frac{1}{2m_{test}} \sum_{i=1}^{m_{test}} \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2$
• For classification ~ Misclassification error (aka 0/1 misclassification error):
  
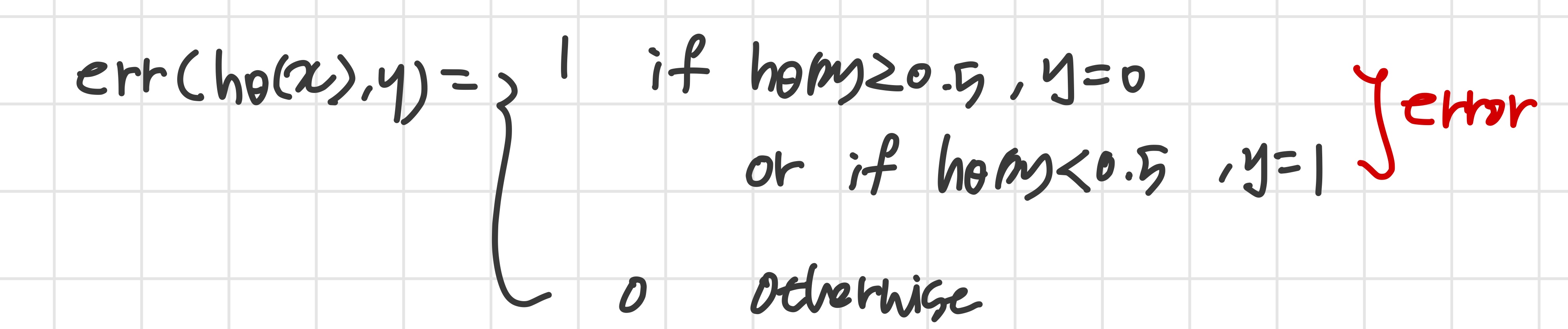
  The average test error for the test set is:
  $Test Error = \frac{1}{m_{test}}\sum_{i=1}^{m_{test}}err(h_\theta(x_{test}^{(i)}, y_{test}^{(i)})$
  를 통해 잘못 분류된 test data의 비율을 알 수 있다.

3) Model Selection and Train/Validation/Test Sets

학습 알고리즘이 training set에 잘 fit 한다고 해서 좋은 가설이라고 할 순 없다.
overfitting 될 수도 있고 새로운 입력값에 대한 예측은 형편없을 수 있기 때문이다. The error of your hypothesis as measured on the data set with which you trained the parameters will be lower than the error on any other data set.
'파라미터를 훈련시키는데 사용한 data로 hypothesis를 평가하면 당연히 결과는 좋을 수 밖에 없다'
따라서 training set를 총 3개로 나눈다.

Evaluating hypothesis

---

training set => training set (60%) + cross validation set (20%) + test set (20%)

Train / validation / test error

---

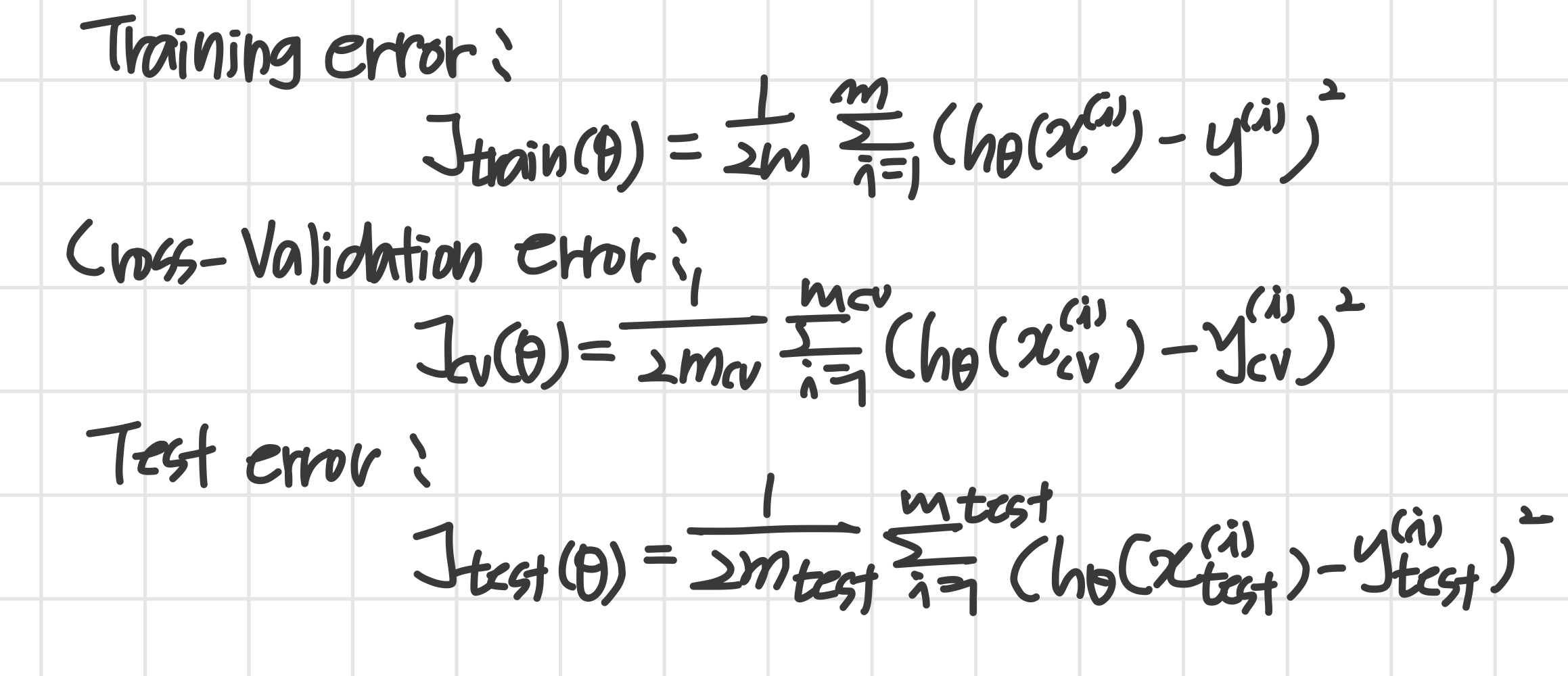
Model Selection

---

모델을 선택할 때 validation set를 사용한다.


1. Optimize the parameters in $\Theta$ using the training set for each polynomial degree.
'training set로 최적의 파라미터를 찾는다'
2. Find the polynomial degree d with the least error using the cross validation set.
'위에서 구한 최적의 파라미터와 cross validation set로 에러가 가장 적은 h를 찾는다.'
3. Estimate the generalization error using the test set with $J_{test}(\Theta^{(d)})$ , (d = theta from polynomial with lower error);
'test set 넣어서 실행해 보기'