[ML] 8주차-1 : Clustering

Machine Learning by professor Andrew Ng in Coursera

1) Unsupervised Learning: Introduction

Supervised Learning

---

'decision boundary를 찾는 게 목표'

Unsupervised Learning

---

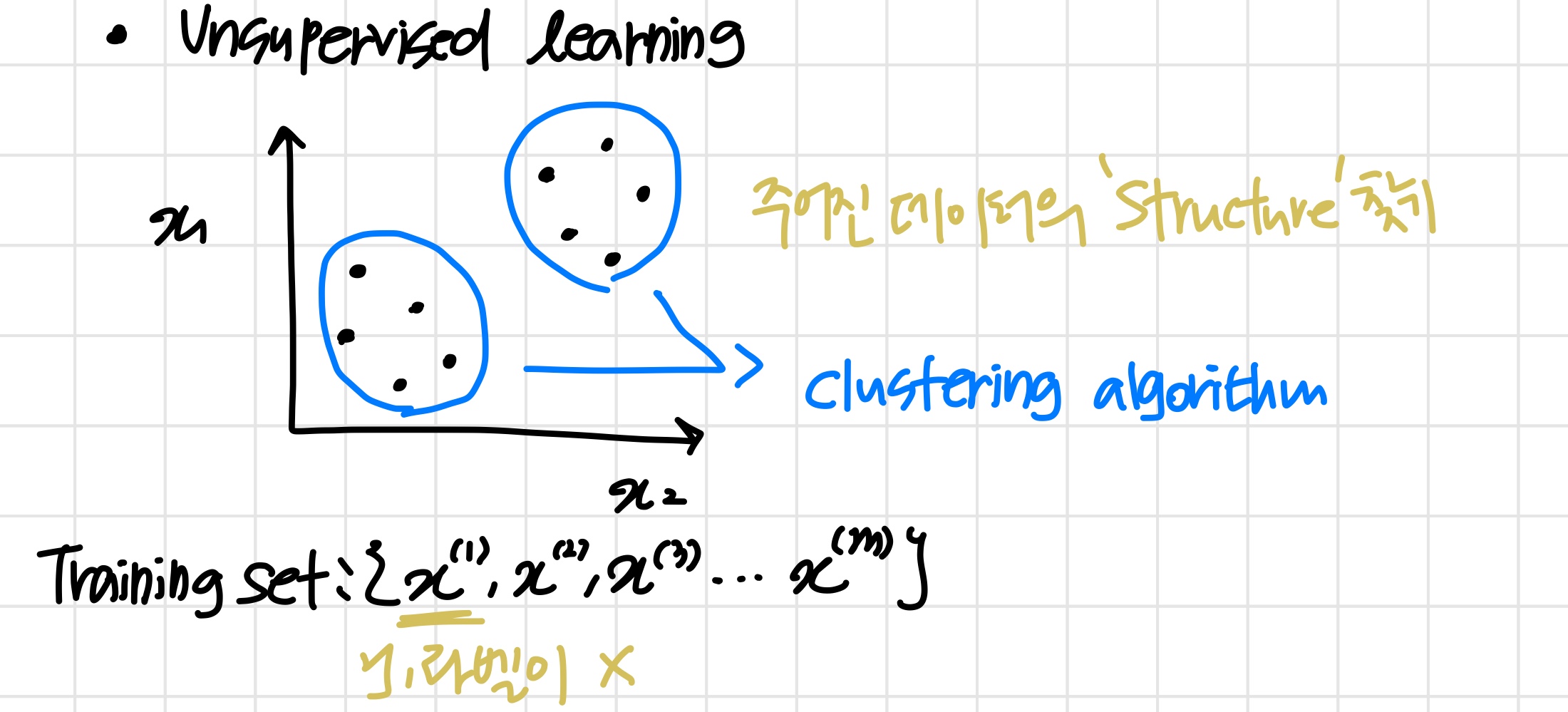
2) K-Means Algorithm

'가장 널리 쓰이는 clustering algorithm'

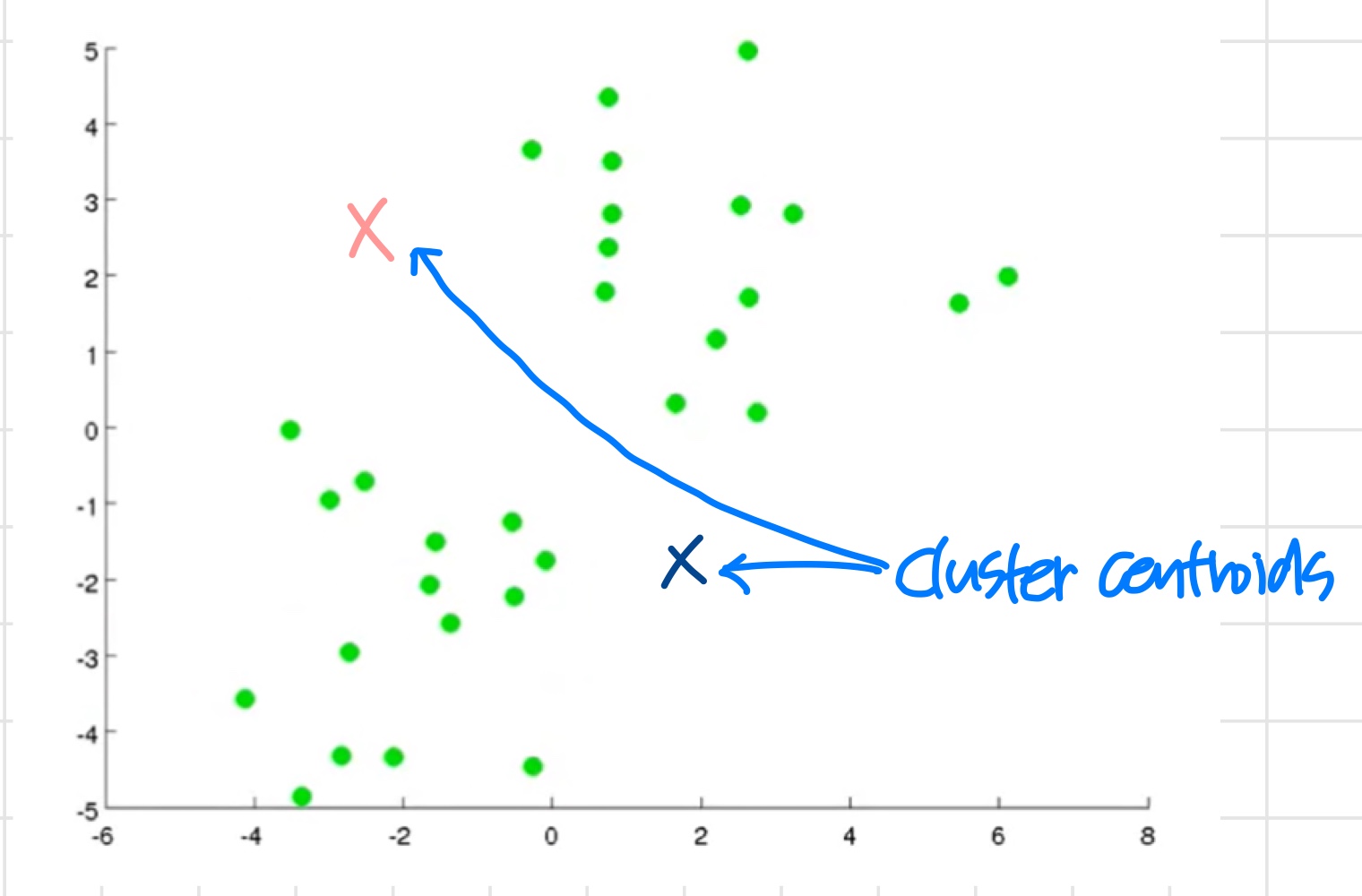
위와 같이 주어진 연두색 데이터들을 2개의 cluster로 나누고자 한다.

• 우선 랜덤으로 cluster centroids가 될 x와 x를 초기화한다.
• K-Means algorithm이 이때 하는 일
  • cluster assignments
  • move centroid step
  • 연두색 점들을 전부 돌면서 x와 x 중 더 가까운 것을 해당 점의 cluster centroid로 지정한다.

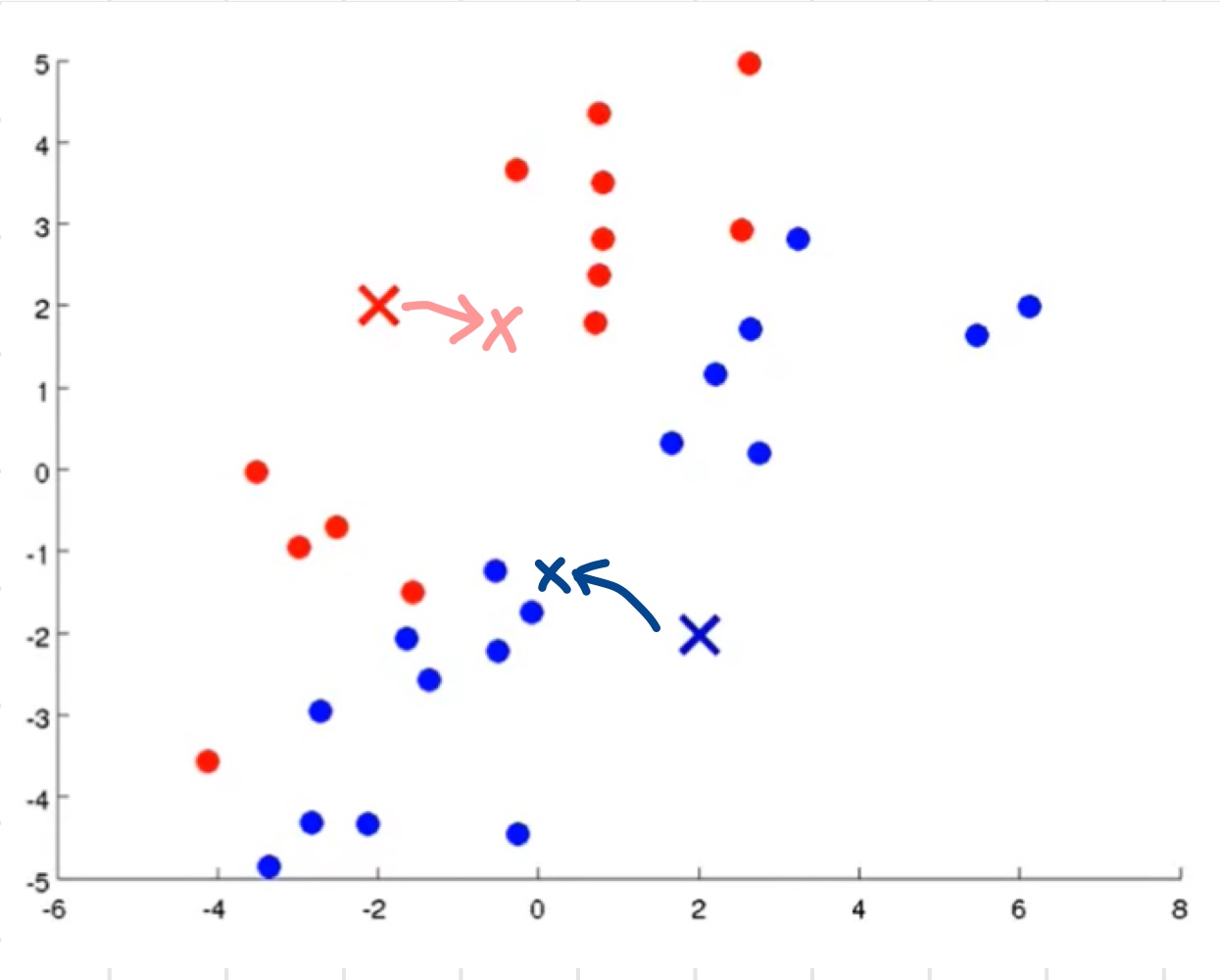
• 이제 x와 x를 centroid로 지정한 데이터들 간의 평균을 구하고 그 위치로 이동시킨다.
• 바뀐 centroid를 기준으로 다시 모든 데이터를 돌며 더 가까운 것을 해당 데이터의 cluster centroid로 지정한다.

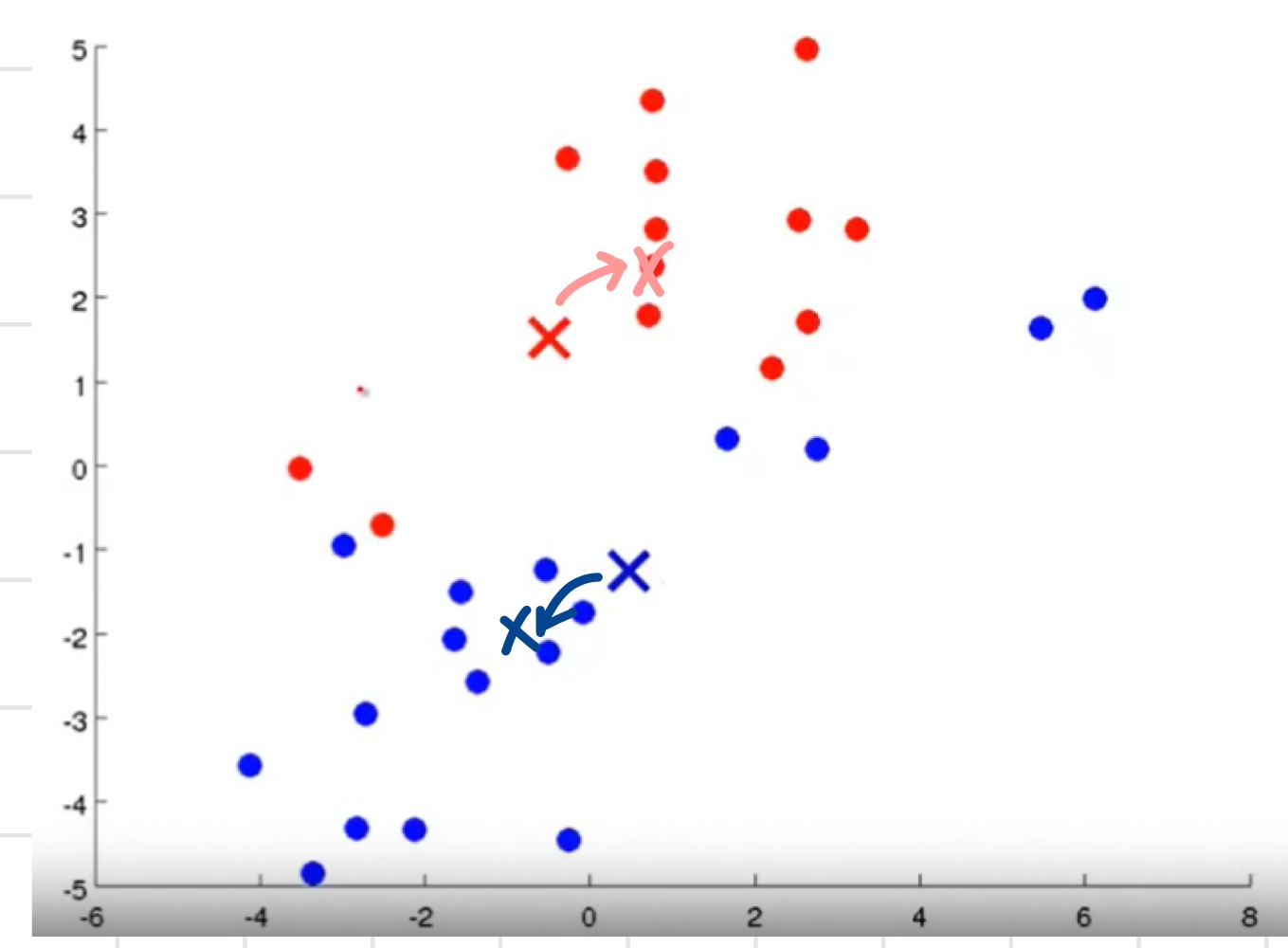
• 위의 과정을 반복.
  즉 다시 빨/파 그룹의 평균을 내고 centroid를 각각의 새로운 평균 위치로 이동시킴.
• 반복하다보면 centroid들의 위치가 더 이상 바뀌지 않는 시점이 온다.
  

K-means algorithm

---

K-means for non-separated clusters

---

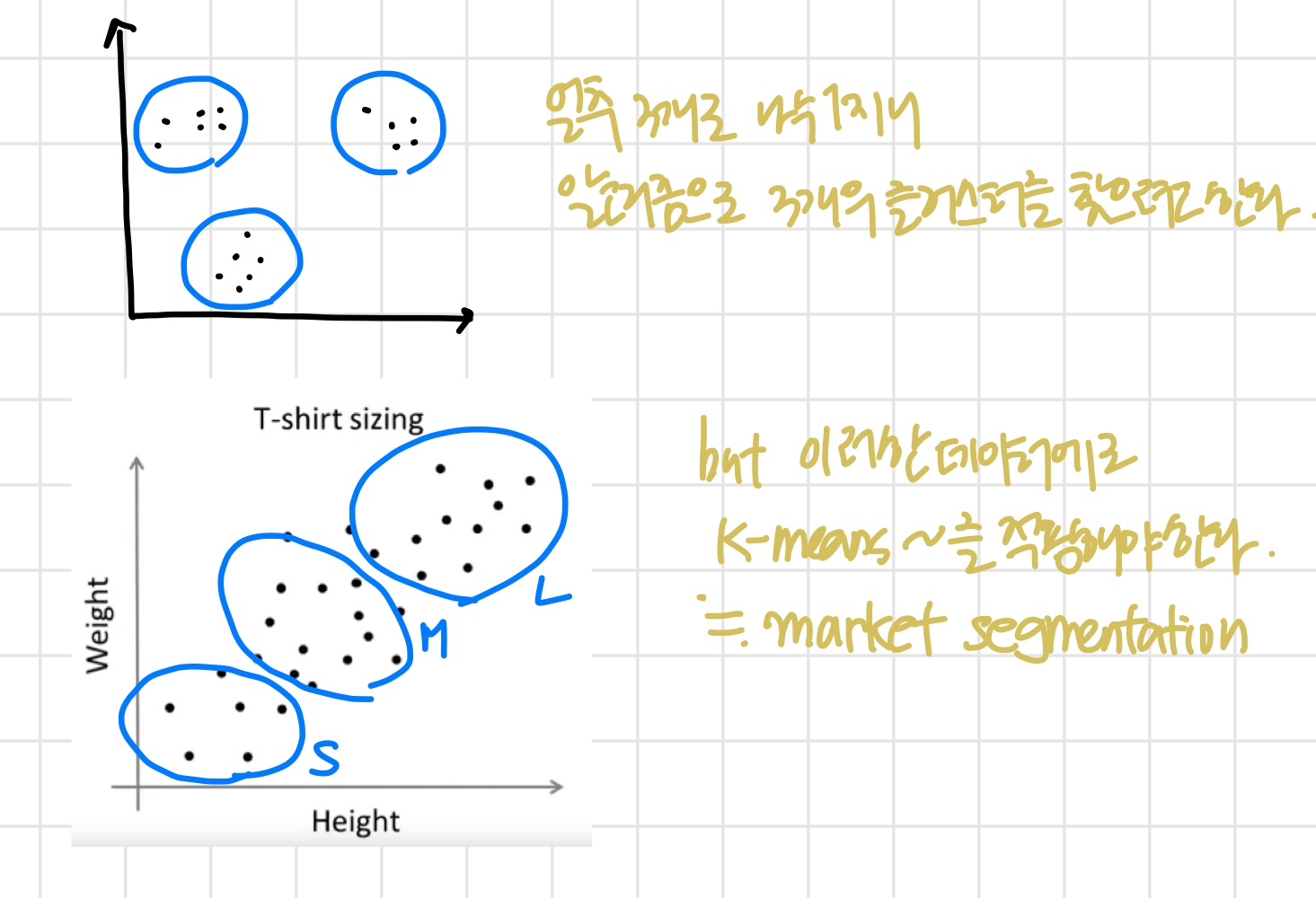
3) Optimization Objective

K-means optimization objective

---

• $c^{(i)} = \text{index of cluster (1, 2, ...k) to which example } x^{(i)} \text{ is currently assigned.}$
• $\mu_k = \text{cluster centroid k }(\mu_k\in R^n)$
• $\mu_{c^{(i)}} = \text{cluster centroid of cluster to which example } x^{(i)} \text{ has been assigned.}$
  

K-means algorithm

---

4) Random Initialization

K-means algorithm

---

• Randomly initialize $K$ cluster centroids $\mu_1, \mu_2, ...., \mu_K \in R^n$
  '어떻게 랜덤하게 초기화할 지에 대해 알아본다.'
• Repeat {
  ' step1 : cluster assignment '
  for $i$=1 to $m$
  $c^{(i)}$ := index (from 1 to $K$) of cluster centroid closest to $x^{(i)}$
  ' step2 : move centroid '
  for $k$ = 1 to $K$
  $\mu_k$ := average (mean) of points assigned to cluster $k$
  }

Random initialization

---

• 반드시 $K < m$
  '$K$는 센트로이드 개수, $m$은 훈련세트 개수 '
• $K$개의 훈련 샘플을 랜덤하게 고르고 $centroid$로 설정한다.
• $\mu_1, \mu_2, ...\mu_K$값을 위에서 고른 $K$개의 훈련 샘플과 동일하게 설정한다.

Local optima

---

'k-means can end up in local optima'

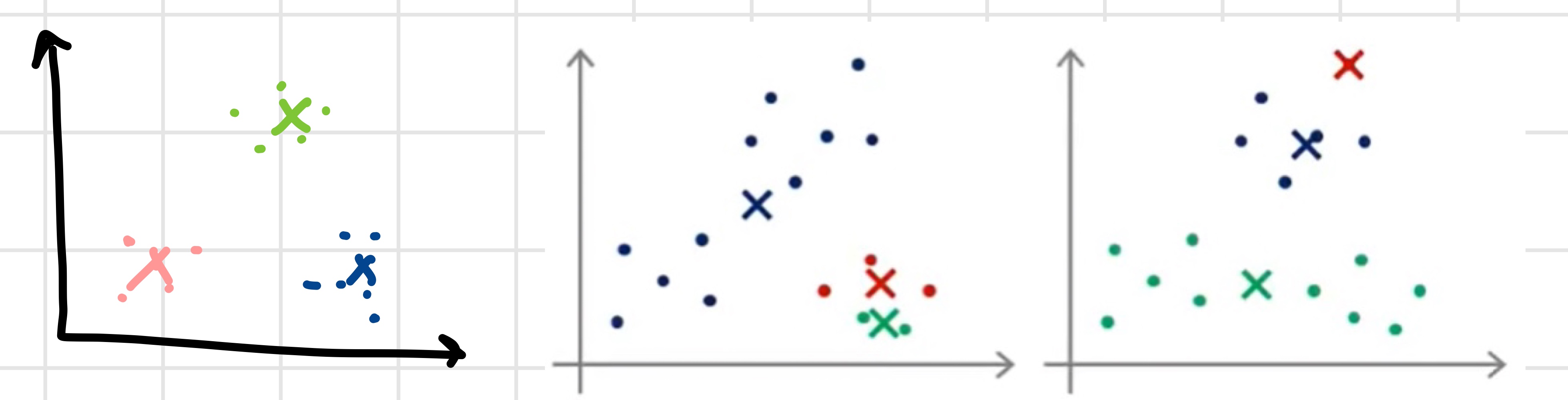
위의 두 번째, 세 번째 그래프와 같이 $\text{local optima}$에 갇힐 수 있다.
이때 랜덤 초기화를 여러 번 반복함으로써 문제를 해결한다.

Random initialization

---

Choosing the number of clusters

---

'사실 automatic한 최고의 방법은 없다고 한다. 가장 많이 쓰는 방법은 데이터들이 시각화된 것을 보고 manually 고르는 것이다.'

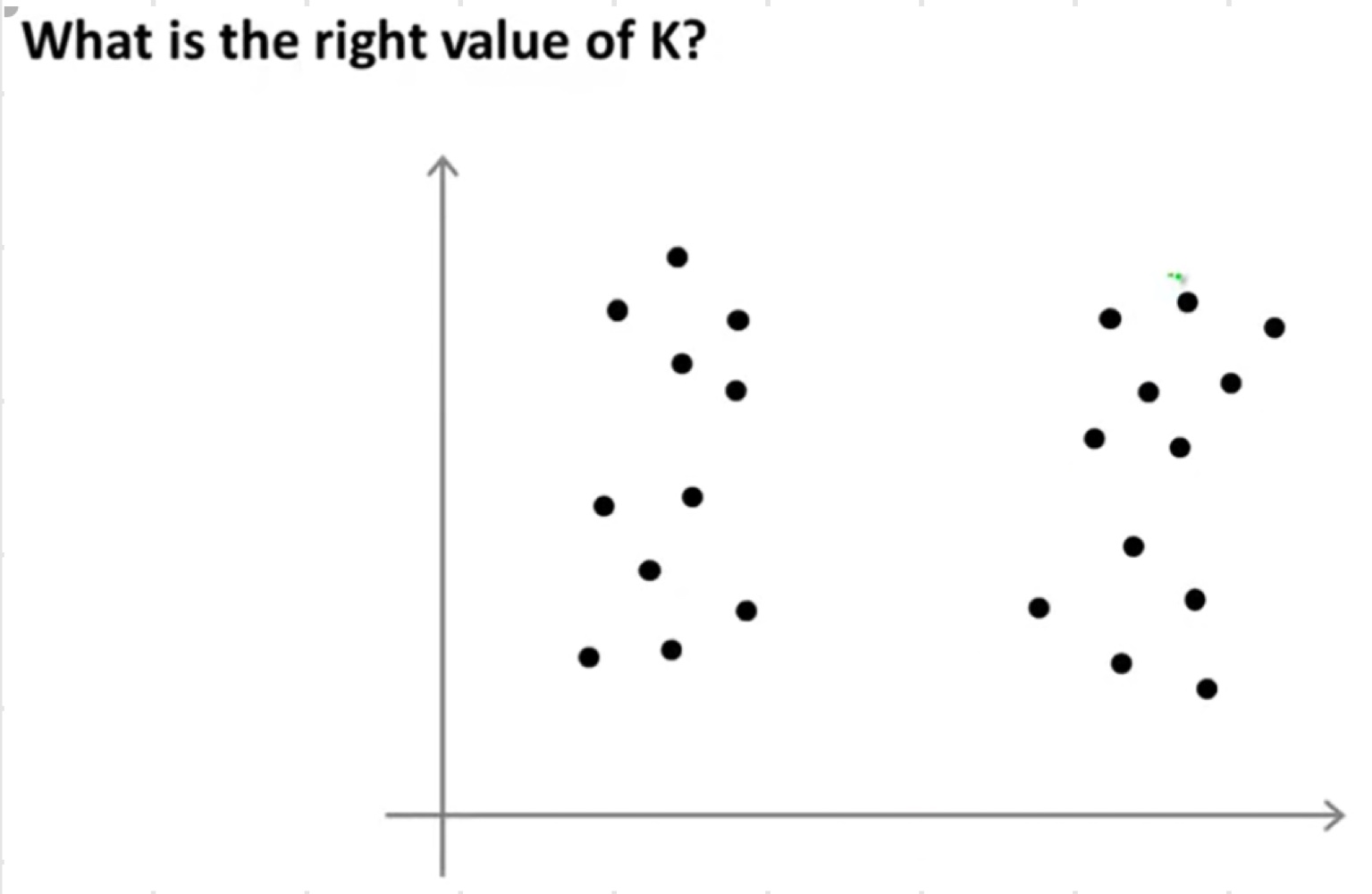
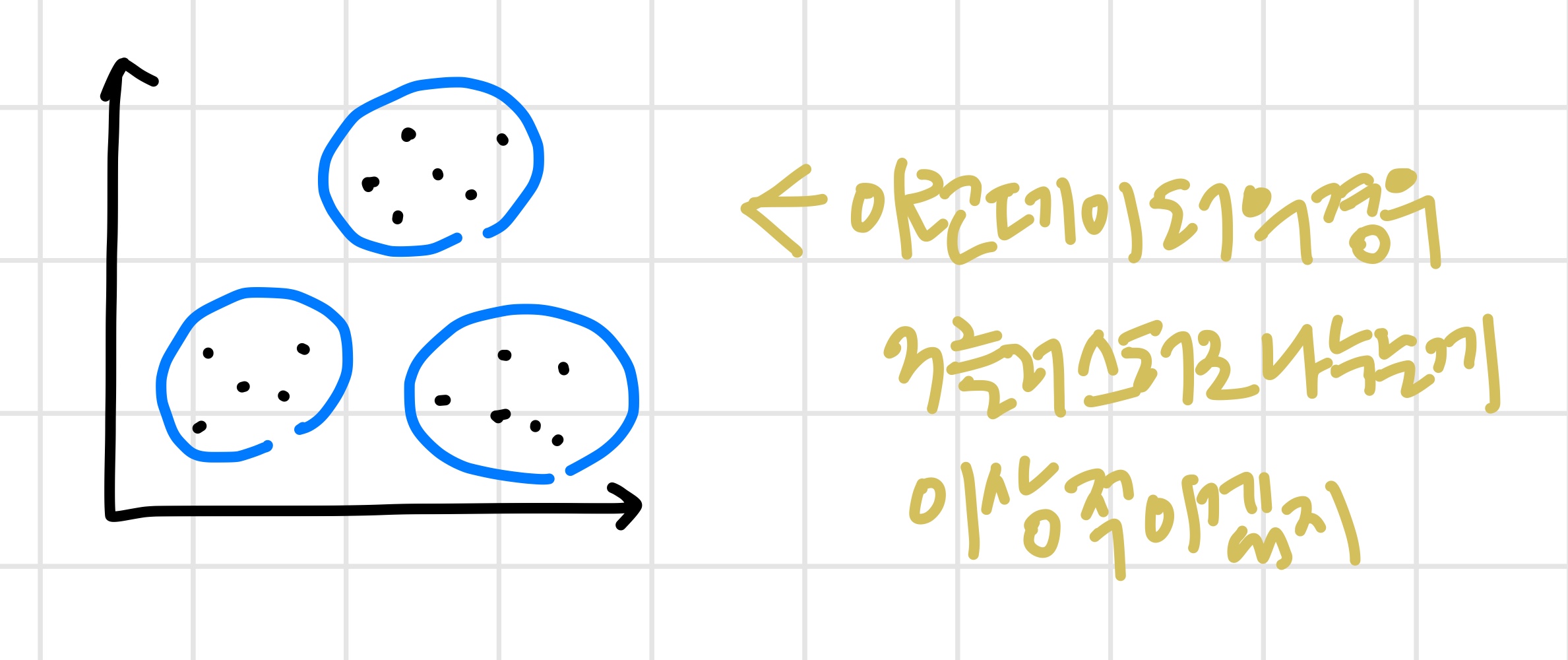
' 라벨이 없기 때문에 더 어렵다. 위의 그래프를 보고 어떤 사람은 2개의 cluster로 보고 또 다른 사람은 4개의 cluster로 보기도 한다. '

Choosing the value of K

---

Elbow method

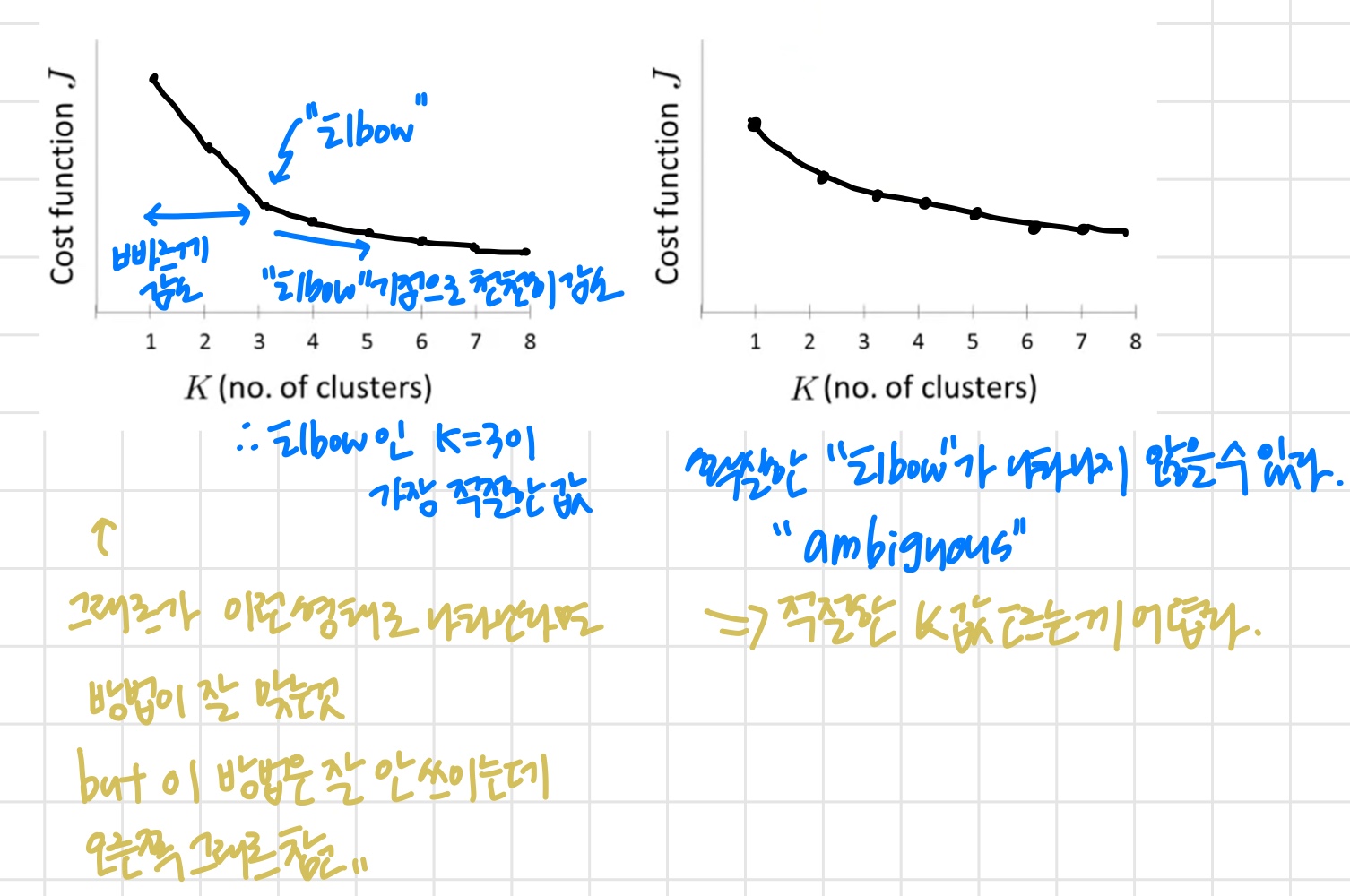
'Elbow 방법이 항상 적절한 것은 아니다. 그때의 목적에 따라 적절한 방법으로 cluster 개수를 결정한다.'

Q : k-means 알고리즘을 실행했다. 이때 함수 $J$의 값이 k가 3일때보다 5일때 훨씬 컸다. 어떻게 할까?
k=5 에서 알고리즘을 실행했을 때 나쁜 $\text{local minimum}$에 갇힌 것으로 볼 수 있다. 랜덤 초기화를 반복하면서 k-means를 다시 실행해 본다.