5.2 Feedback- Carrier Phase Synchronization -1(Data-Aided)

앞서 PLL을 설명할 때는 상수 phase offset을 설정하고 PLL이 상수 phase로 수렴하는 것을 확인했다.

그러나 실제 carrier phase offset의 경우 매 심볼 주기 마다 다른 phase soffset이 존재한다.

따라서 수신부에서 매치드 필터링된 이후 심볼 주기에서 샘플을 뽑았을 때 phase offset는 계속해서 달라진다. 이를 아래 식으로 나타낸다.

따라서 carrier phase 동기화 부분은 매 심볼 간격으로 변화하는 phase인 $\theta_\triangle$을 추적해야 한다.

회전변환 공식에 따르면 시계방향 회전은 $Icos\theta+Qsin\theta$ 와 $Qcos\theta-Isin\theta$ 를 각가 I와 Q에 곱해주면 된다.

따라서 매 심볼 간격으로 추정된 phase offset만큼 회전변환 시켜주면서 carrier phase synchornization을 수행하게 된다 식은 아래와 같다.

이제 앞선 feedforward carrier phase synchronization에서 phase offset을 유도했던 식을 살펴보면 아래와 같다.

이제 이전 PLL의 phase error detector의 함수를 위 식으로 바꿔주기만 하면 feedback 기반 carrier phase synchronization이 완성된다.

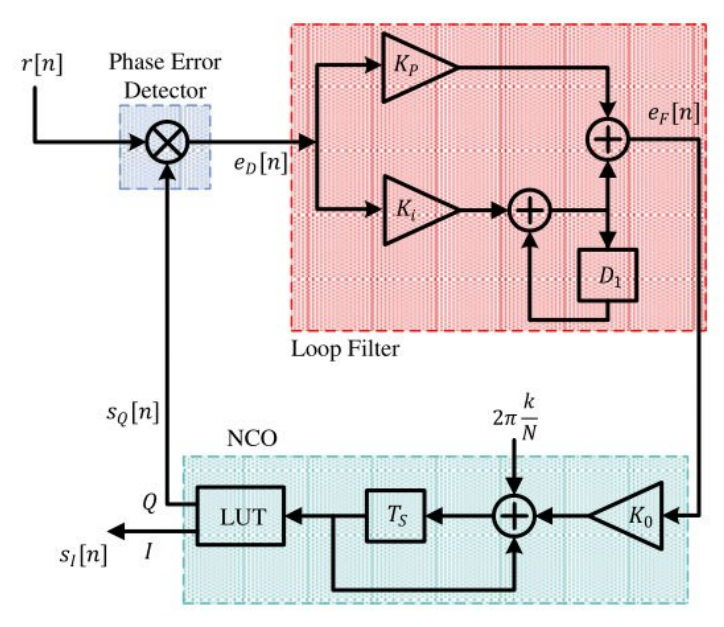
따라서 위 그림에서 Phase Error Detector의 출력인 $e_D[n]$은 아래 식과 같다.

따라서 위 식을 풀면

따라서 phase error detector의 출력은 아래와 같다.

이제 feedback 기반 carrier phase synchornization의 구조를 아래 그림에 나타낼 수 있다.

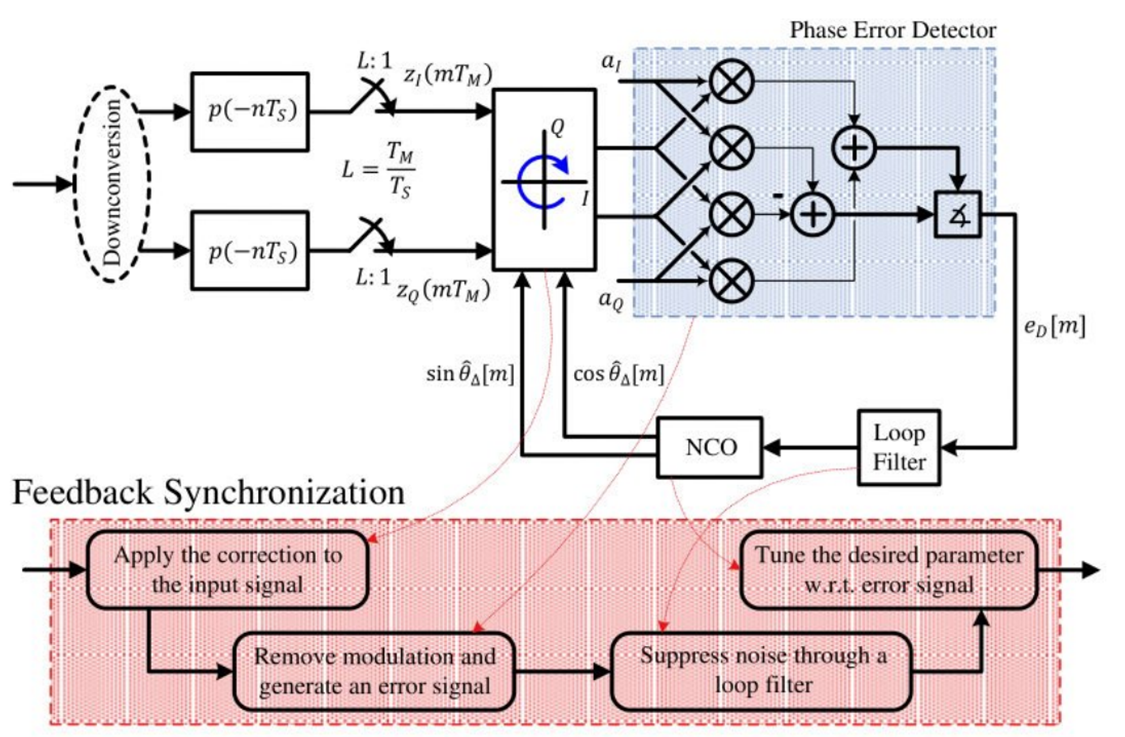
feedforward 기반 carrier phase synchronization은 carrier phase offset을 찾아 한 번에 보상하는 방식으로 이루어졌다.

반면 feedback 기반 carrier phase synchronization은 carrier phase offset을 찾은뒤 loop filter를 통해 점진적으로 수렴하는 방식이다.

loop filter는 대역 외에 존재하는 노이즈와 신호 외 다른 주파수 성분을 억제한다.

NCO 또는 DDS라고 불리는 하드웨어는 다음 심볼 주기에 추정된 심볼 위상만큼 회전 시키는 정현파를 생성한다.

즉 PLL과 차이점은 phase error detector 가 다르고 또 매 심볼 주기마다 위상을 보정해준다는 차이가 존재한다.

이제 feedback 기반 carrier phase synchronizer의 phase error detector를 분석해보자.

PLL과 비슷하게 S-curve 또는 mean curve라고 불리는 것을 활용할 수 있다.

실제 phase offset인 $\theta_\triangle$ 이랑 추정 phase offset인 $\hat{\theta_\triangle}$의 오차를 $\theta_{\triangle:e}$라고 하자.

이 때 feedback 기반 carrier phase synchronizer의 phase error detector의 평균 출력 $\bar{e_D}$는 아래와 같다.

따라서 phase error detector의 gain은 $k_D = 1$ 이다.

이제 phase error detector의 s-curve를 보면 아래와 같다.

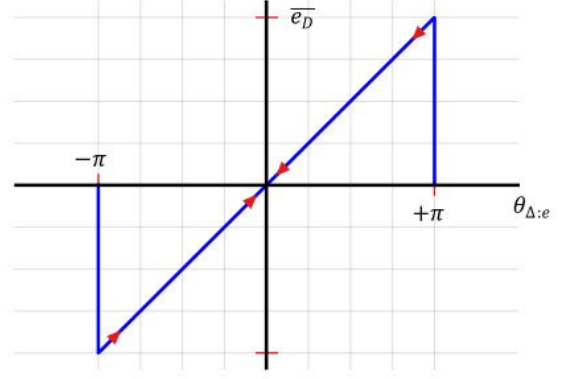
S-curve는 $-\pi <= \theta_{\triangle:e} <= \pi$ 에서 선형 특성을 갖는다. 그리고 양수 기울기가 $\theta_{\triangle:e} =0$ 근처에서만 나타난다. 따라서 최종 lock 된 추정 phase의 모호성이 없다.

참고하자면 S-curve가 양수일 때 phase가 lock 특성을 보인다.