Perceptron

퍼셉트론(Perceptron)은 인공 신경망(Aritificial Neural Network, ANN)의 구성 요소로서 다수의 값을 입력받아 하나의 값으로 출력하는 알고리즘이다. 퍼셉트론(Perceptron)은 perception과 neuron의 합성어이며 인공 뉴런이라고도 부른다.

즉, 퍼셉트론은 생물학적인 신경계(Neual Network)의 기본 단위인 신경세포(=뉴런)의 동작 과정을 통계학적으로 모델링한 알고리즘이다.

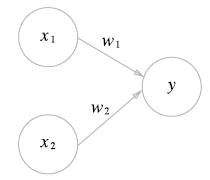
Biological neuron model

뉴런은 신경계를 구성하는 세포이며, 인접한 다른 뉴런과 다양한 신호(=자극)를 주고받으며 정보를 얻거나 저장하는 역할을 한다.

뉴런은 수상돌기에서 인접한 다수의 뉴런 내 축삭돌기와 시냅스를 통해 신호를 입력받아 신경세포체에 저장하는데 이때 해당 뉴런이 저장한 신호의 크기가 특정 값(=임계값) 이상이 될 때만 신호가 축삭돌기를 통해 외부로 전달되기 때문에, 출력신호를 제어할 수 있다.

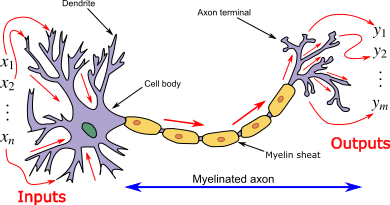
1. 자극(input data)이 synapse(weight)를 통해서 cell body(function)로 들어오게 된다.

2. cell body(function)에서 threshold(임계치)를 넘게 되면 연결된 다른 neuron으로 output value를 전파한다.

3. output value는 연결된 neuron의 synapse를 통과하여 또 새로운 전파를 만들어낸다.(다층 신경망의 개념)

Artificial neuron model

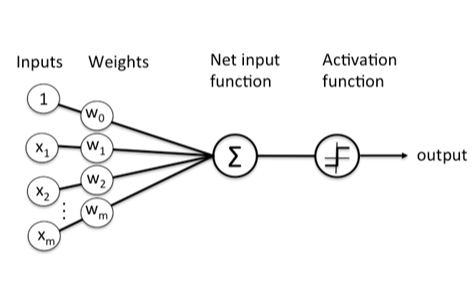
x는 입력 신호, output은 출력 신호, w는 가중치(weight)를 의미하고 원을 뉴런 또는 노드라고 부른다.

입력 신호가 뉴런에 보내질 때는 각각 고유한 가중치가 곱해진다(w1x1+w2x2).

뉴런에서 전달 받은 신호의 총합이 활성화함수(activation function)을 거쳐 임계값을 넘을 때만 을 출력한다.

이것을 수식으로 나타내면, 아래와 같다.

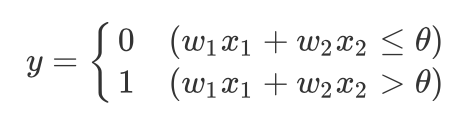
퍼셉트론은 복수의 입력 신호 각각에 고유한 가중치를 부여한다. 가중치는 각 신호가 결과에 주는 영향력을 조절하는 요소로 작용하며, 가중치가 클수록 해당 신호가 그만큼 더 중요함을 뜻한다.

퍼셉트론을 이용한 논리회로

AND

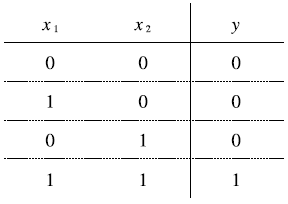
위의 표는 AND게이트의 진리표이며 이 AND게이트를 퍼셉트론으로 표현하기 위해서는 진리표대로 작동하도록하는 w₁, w₂, θ 의 값을 적절하게 정해야 한다.

import numpy as np

def AND_basic(x1, x2):
   w1, w2, theta = 0.5, 0.5, 0.7
   tmp = x1*w1 + x2*w2
   if tmp <= theta:
       return 0
   elif tmp > theta:
       return 1
       
inputs = [(0, 0), (1, 0), (0, 1), (1, 1)]
 
for x1, x2 in inputs:
   y = AND_basic(x1, x2)
   print('({x1}, {x2}) -> {y}'.format(x1=x1, x2=x2, y=y))
(0, 0) -> 0
(1, 0) -> 0
(0, 1) -> 0
(1, 1) -> 1

NAND, OR

NAND 게이트는 Not AND를 의미하며 AND 게이트의 출력을 반대로한 것과 같다.

OR 게이트는 입력 신호 중 하나 이상이 1이면 출력이 1이 되는 논리 회로다.

위의 각 게이트(AND, NAND, OR)의 진리표들을 보면, 퍼셉트론 구조는 모두 동일하며 다른것은 매개변수()의 값뿐이다. 따라서, 매개변수의 값만 적절히 조정하면 AND, NAND, OR을 구현할 수 있다

# NAND
def NAND(x1, x2):
   x = np.array([x1, x2])
   w = np.array([-0.5, -0.5])
   b = 0.7
   tmp = np.sum(w*x) + b
   if tmp <= 0:
       return 0
   else:
       return 1

# OR
def OR(x1, x2):
   x = np.array([x1, x2])
   w = np.array([0.5, 0.5])
   b = -0.2
   tmp = np.sum(w*x) + b
   if tmp <= 0:
       return 0
   else:
       return 1
       
inputs = [(0, 0), (1, 0), (0, 1), (1, 1)]

print('NAND :')
for x1, x2 in inputs:
   y = NAND(x1, x2)
   print('({x1}, {x2}) -> {y}'.format(x1=x1, x2=x2, y=y))
   
print('OR :')
for x1, x2 in inputs:
   y = OR(x1, x2)
   print('({x1}, {x2}) -> {y}'.format(x1=x1, x2=x2, y=y))
NAND :
(0, 0) -> 1
(1, 0) -> 1
(0, 1) -> 1
(1, 1) -> 0
OR :
(0, 0) -> 0
(1, 0) -> 1
(0, 1) -> 1
(1, 1) -> 1

XOR

XOR 게이트는 베타적 논리합 이라는 논리 회로다.

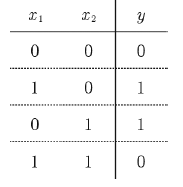
단층 퍼셉트론으로 AND, NAND, OR 게이트는 구현 가능하지만, XOR 게이트는 구현할 수 없다. 퍼셉트론은 아래와 같이 직선 으로 나뉜 두 영역을 만든다. 하지만 XOR은 직선으로 두 영역을 나눌 수 없다.

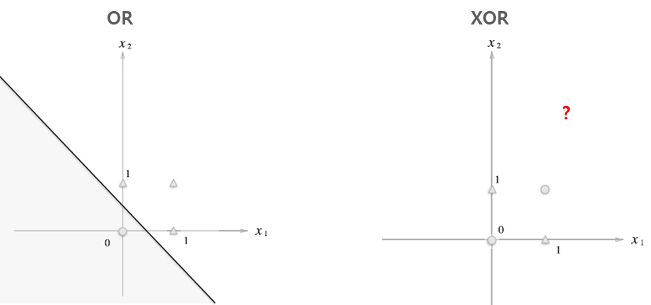
XOR 한계를 해결하는 방법은 바로 1차원인 좌표 평면 자체에 변화를 주는 것 이다.

퍼셉트론의 한계가 발표된 이후 10년이 지난 후에 이 문제가 해결되는데 XOR 문제를 해결하기 위해서는 두 개의 퍼셉트론을 한 번에 계산할 수 있어야 하는데, 이를 가능하게 하려면 숨어있는 층, 은닉층(Hidden layer)을 만들면 된다. 은닉층을 만들어 공간을 왜곡하면 두 영역을 가로지르는 선을 만들 수 있다.

이러한 개념이 여러 개의 퍼셉트론을 층 구조로 구성한 신경망 모델인 다층 퍼셉트론(multilayer perceptron)이다.

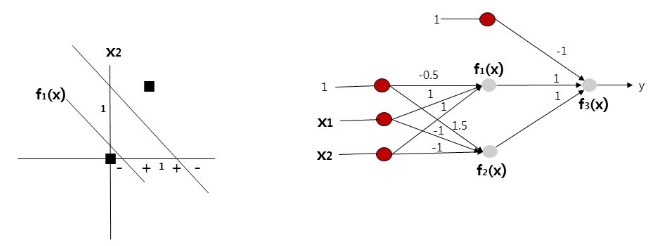
def XOR(x1, x2): 
	s1 = NAND(x1, x2) 
	s2 = OR(x1, x2) 
	y = AND(s1, s2) 
	return y 

for i in [0, 1]: 
	for j in [0, 1]: 
		print(f'{i, j}', end=' ') 

print() 
print('XOR : ', end = '') 

for i in [0, 1]: 
	for j in [0, 1]: print(XOR(i, j), end = ' ')
(0, 0) (0, 1) (1, 0) (1, 1) 
XOR : 0 1 1 0