[EECS 498-007 / 598-005] 4. Regularization + Optimization

이번 포스팅은 제가 블로그에 hands-on ML 책의 gradient descent내용을 정리한 포스팅과 같이 보시면 좋습니다 ^^.
[Hands-on Machin Learning] Gradient Descent
저번 강의에서 linear classifier의 score를 SVM loss, corss-entropy loss(softmax)를 사용한 loss 와 model의 overfitting을 방지하기위한 regularization을 더해주는 형태가 최종 L(W) 즉 loss function 이라는 것을 알아보았다.
그렇다면 linear classifier 와 loss function이 주어졌을때 우리는 어떻게 해당 loss를 만족하는 weights matrices 를 찾아갈 것인가?
( how do we find the best W? )Optimization
일반적인 의미로 loss function을 최소화 시키는 weights matrices W를 찾아가는 과정을 optimization이라고 한다.
* 이번 포스팅에서는 loss function을 단순히 weight matrix를 input으로 갖고 output으로 loss에대한 scalar value를 반환하는 abstract function으로서 볼것이다.
Optimization은 직관적으로 보면 우리가 크고 우거진 산의 계곡에서 눈을 가린채로 산 아래까지 찾아가는 과정으로 생각해볼 수 있다.
우리가 산에서 아래로 내려가는 방법은 단순하게 밑을 향해간다 라고 생각할 수 있지만 일반적으로 이러한 문제는 엄청 어렵다 그래서 실제로 우리는 다양한 iterative한 방법을 통하여 접근한다.
Idea1. Random search (bad idea!)
# Assume X_te is [3073 x 10000], Y_te is [10000 x 1]
scores = Wbest.dot(Xte_cols)
# find the index with max score in each cloumn (the predicted class)
Yte_predict = np.argmax(scores, axis = 0)
# and calculate accuracy (fraction of predictions that are correct)
np.mean(Yte_preddict == Yte)
# returne accuracy위 코드는 weight matrix에 해당하는 많은 random value를 만들어내고 각기 다른 matrix별 loss를 구한 후 lowest value를 찾아가는 과정을 반복하는 것이다.
또한 위 코드는 이전에 찾은 best W matrix와 test data를 dot prodoct 하여 나온 score 에서 가장 큰 (가장 좋은) 값들을 찾아 평균을 내주는 과정이다.
* 사실 이러한 코드는 성능이 매우 좋지 않다.
Idea2. Follow the slope
두번째로 살펴볼 방법은 local geometry 한 방법을 사용하는 것이다.
우리가 산 속에서 앞을 볼 수 없는 사람이라고 생각해 봤을때 산의 밑바닥이 어디인지 알 수 없지만, 주변을 돌아다니면서 얻은 정보를통해 어디가 밑으로 향하는 길인지 판단하고 진행하며 반복하여 밑으로 가는 방법이다.
In 1-dimension, the derivative of a function gives the slope
위의 수식은 매우 단순해 보이지만 꽤 잘 동작하는 알고리즘 수식이다.
singel scalar value를 input으로, single scalar value를 output으로 반환하는 형태로 어떤 x ( point ) 에서의 derivative 즉 slope(gradient)를 구하는 형태이다.
위 수식의 input x 를 scalar 가 아닌 vector로 바꿔 본다면 multiple demension으로 확장시켜 다변수 함수로 볼 수 있고 input vetor에 대하여 gradient의 집합인 vector 를 output으로 반환하는 형태가 된다.
위의 수식을 토대로 직접적으로 limit definition of the gradient를 구해보자.
위 그림에서 왼쪽의 vector는 현재의 weight matrix W이고 오른쪽은 우리가 계산하고자하는 weight matrix에 대한 loss의 gradient이다. 이때 loss 는 single scalar value이고 loss의 gradient는 weight matrix와 같은 shape를 갖은 slope라고 말하는 gradient vetor이다.
gradient의 limit definition 과정을 numerical하게 실행해 보자.
위 그림처럼 현재의 w의 첫번째 element 대해 아주 작은 값(h)를 더해 loss를 계산하고 이를 limit definition of the derivative 에 적용시켜 나온 numerical approximation을 gradient vector의 첫번째 element에 집어넣는다. 이 것이 해당 w에 대한 방향 gradient (dL/dW)가 된다.
이러한 방식으로 weight matrix W의 모든 dimension에 대해 반복하여 계산한다.
하지만 이러한 방식은 매우 느리다. 사실 현재의 시스템에서 매우 비효율적이지는 않지만 훨씬 큰 neural network system 에서는 weight matrix가 매우 크기 때문에 비효율적이다. 현실의 W는 매우 많은 parameter를 갖기에 high dimentional optimazation problems에서는 비적합하다.
*calculate an analytic gradient
그래서 우리는 이전과같이 W의 모든 원소를 순회하는 것이 아니라 gradient를 구하는 식만 도출하고(dL/dW) gradient vector를 한번에 계산해버릴 수 있다.
* 실제로는 항상 위와같이 analytic gradient를 사용하지만 디버깅을 위해 numerical gradient를 사용하기도 한다. 이를 위해 아래와같이 pytorch 에서 함수로 제공되고 있다.
Gradient Descent
여태까지 보았듯이 loss fuction을 optimizing 하기위한 전략은 우리가 아무 point에서나 시작해도 local gradient direction을 알게되고 step을 반복하며 negative gradient로 진행을 하며 loss를 줄이는 것 이다.
이 핵심 개념을 간단한 코드를 통해 살펴보자
w = initialize_weights()
for t in range(num_steps):
dw = compute_gradient(loss_fn, data, w)
w -= learning_rate * dw위의 간단한 알고리즘은 우리가 initialized_weights를 통해 아무데서나 시작하고 고정된 num of iteration (num_steps)만큼 루프를 반복하며 매 step마다 현재 위치의 gradient를 계산하고 negative gradient direction으로 조금씩 이동하게된다는 코드이다.
*이 algorithm에는 3가지의 hyperparameter가 있다.
- method of initializing the weights()
: 이 weight를 초기화하는 방법은 다음 강의에서 좀더 적절하고 다양한 방법을 다루게 될 것이다. - num_of_steps()
: iteration 횟수이며 Gradient Descent에서 사용되는 다양한 stopping criteria가 있는데 강의 후반부에 다룬다. - learning_rate()
: 우리가 계산된 gradient를 얼마나 신뢰할 것 인가를 나타내며 이것은 얼마나 크게 움직일것인가를 결정하게 된다. 또한 우리의 알고리즘이 얼마나 빠르게 학습할 것인지를 결정한다.
위 그림은 gradient descent 알고리즘의 진행과정을 heatmap 으로 살펴본 것이다. 이 그림에서는 x 와 y 축에 두개의 weights에 대해서만 나타내었고, 각 color는 loss function의 크기를 나타낸다 (red region이 low loss를 나타냄).
initialized W가 그림의 하단에서 시작되어 loss function의 negative gradient를 매 step마다 찾아가며 진행함을 나타낸다.
이 그림이 나타내는 Gradient Descent algorithm의 특징은 곧장 bottom으로 가지 않는다는 것이다.
Batch Gradient Descent
첫번째 수식은 regularization이 추가된 loss function에 대한 일반적인 형태의 수식이며 이를 미분하여 나온 가 gradient vector를 구하는 식이다.
이 전에 보았던 gradient descent 방식은 data set의 크기가 매우 크다면 매 step에서 전체 training set에 대한 sum of loss를 구하기 때문에 매우 고비용이 되어 비효율적이다.
이러한 문제를 해결하기위한 변형 gradient descent algorithm이 있다.
Stochastic Gradient Descent(SGD)
SGD의 핵심은 loss fuction이 training data set에 대해 전부 계산하지 않고 mini-batch 라는 subsample을 만들어 대략적으로 계산한다. 보통 이러한 subsample의 size는 32, 64, 128을 사용한다고 한다.
* 사실 SGD의 원래 개념은 mini-batch를 사용하는 것이 아닌 전체 training set에서 랜덤하게 뽑은 단 1개의 데이터의 gradient를 계산하고 weight update시키는 방식을 training set 크기만큼 반복하는 것이라 이러한 random성 때문에 stochastic이라는 이름이 붙은 것 이다. 하지만 mini-batch gradient descent가 굉장히 보편화되며 SGD라는 용어가 mini-batch gradient descent를 의미하는 경우가 많아졌다.
코드를 통해 살펴보자
# Stochastic gradient descent
w = initialize_weights()
for t in range(num_steps):
mini_batch = sample_data(data, batch_size)
dw = compute_gradient(loss_fn, mini_batch, w)
w -= learning_rate * dw위 코드는 이전의 gradient descent 코드에서 추가로 매 스텝마다 full training data set를 batch size만큼 sampling 해주어 mini-batch의 gradient를 구하고 w를 update 해준다.
여기서 원래의 initialized weights, num of steps, learning rate에서 새로운 hyperparameter인 batch size가 추가되었다.
* batch size라는 하이퍼파라미터는 다른 하이퍼파라미터보다 모델이 덜 민감하게 반응한다고한다.
SGD에서는 loss function을 확률론적으로 접근하기때문에 stochastic 이라는 이름이 덛붙여졌다. 우리가 data set을 확률분포로 부터 샘플링된 것으로 생각했을때 우리는 loss function을 모든 가능한 sample들에 대한 expectation으로 생각할 수 있고 아래의 수식과 같이 표현 할 수 있다.
* 이 알고리즘의 본질적인 생각은 결정론적일 수도 있는 문제를 해결하기 위해 무작위성을 이용하는 것이다
이러한 방법에서 loss function을 생각해봤을때 full expectation의 근사치를 계산하기 위해서는 우리가 얼만큼의 sample을 취할지 결정 해야한다.
Problems with SGD
SGD algorithm에는 몇가지 문재가 발생 할 수있다.
-
만약 아래의 loss의 contour plot(등고선) 처럼 (like taco shell) loss의 landscape가 한 방향으로는 빠르게 변하고 다른 방향으로는 천천히 변해간다면 어떻게 될까??
-
이때 gradient descent는 어떻게 움직일까?
step size가 클 수록 아래 그림과 같이 step에 따른 matrix W 의 변화가 진동을하며(zigzag pattern을 보이며) 변화 할 수 있다.
이러한 문제에서 trade-off 가 존재한다.
SGD에서 step size를 크게 할 경우 위처럼 zigzag pattern을 보이고 이런 overshooting을 방지하기위해 step size를 작게할 경우 algorithm이 매우 느리게 수렴하게된다.
이 trade-off로 Loss function이 높은 condition number를 갖게된다.
* condition number란 입력값의 작은변화에대한 출력값의 변화의 정도를 측정하는 지표로 시스템이 민감한 정도를 정량적으로 보여주는 값을 뜻한다.
* 추가로 강의에선 이 경우엔 헤시안 행렬에서의 가장 큰 singular value와 가장 작은 singular value의 비율이 매우 높아진다고 한다.
Local Minima & Saddle point
SGD는 또한 local minimum와 saddle points문제가 나타날 수 있는 알고리즘이다.
local minima 는 zero gradient를 갖지만 사실 bottom of the function은 아닌 point 를 말한다. (global minimum point 가 아닌 local minimum point). algorithm이 step을 진행하다 이 local minimum을 만나 학습을 종료 시키는 경우 문제가되는 것이다.
위의 그림처럼 2-dimension 에서는 local minimum에 갇히는것이 주된 문제일 수 있다. high dimensional optimization에서는 모든 방향에서 gradient가 위로 향해야 해서(loss가 증가해야해서) 이러한 local minimum은 흔치 않지만 high dimensional 에서는 훨씬 흔히 나타나는 saddle point가 문제가 된다.
아래의 그림처럼 어떤 방향으로는 loss가 증가하고 다른 방향으로는 감소하는 지점에서 gradient가 0가 되는 지점을 saddle point라고 한다.
saddle point보다 더 문제가 있는 monkey saddle형태가 아래와 같은 그림처럼 나타나는데 이는 saddle point뿐만 아니라 그 주변에서 평평한 형태를 지니기에 algorithm이 그 곳에서 안주 할 가능성이 높아지고 더디게 진행 될 수 있다.
SGD의 또 다른 문제로 SGD는 gradient를 계산할 때 small estimate of full data set만을 사용하기때문에 모든 step에서의 gradient가 bottom으로 향하는 올바른 direction과는 상관관계가 없어 아래의 그림에서 볼 수 있듯이 noisy하다는 것 이다.
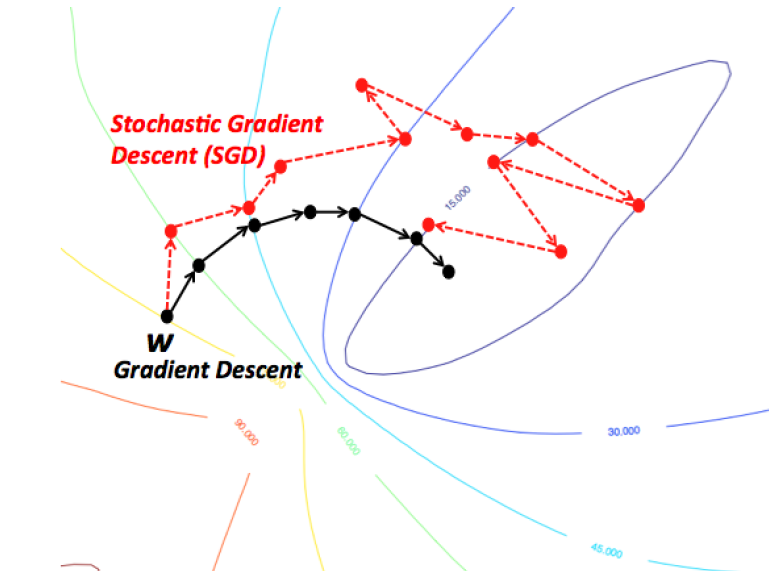
이러한 여러 문제들을 해결하기위해 좀더 똑똑한 SGD version를 통해 개선된 Optimizer를 사용해야 한다.
SGD + Momentum
우리는 이 전에 보았던 taco shell landscape 문제에서 처럼 한 방향(가파른 방향)으로는 빠르게 변화하고 다른 방향(완만한 방향)으로는 천천히 움직이는 문제가 발생하지 않고 가운데의 완만한 방향을 통해 움직이기를 바란다.
이때 등장하는 개념이 바로 Momentum이다.
Momentum 의 핵심 idea는 weight를 업데이트 할 때 이 전에 계산한 gradient도 반영을 해주자는 것이다.
이전의 SGD를 다시 살펴보면 SGD에서는 모든 iteration동안 mini-batch sample에서 계산된 gradient를 통해 weight를 update시키는 방식이었다.
for t range(num_steps):
dw = compute_gradient(w)
w -= learning_rate * dw반면에 SGD + Momentum 에서는 이전의 움직인 방향을 뜻하는 velocity vector를 update에 적용시킨다.
이때의 velocity vector는 historical moving average of gradient를 뜻한다.
* 아래의 momentum 식이 통계학에서 EMA(Exponential Moving Average) 또는 EWMA(Exponential Weighted Moving Average)를 뜻한다고 한다.
v = 0
for t in range(num_steps):
dw = compute_gradietn(w)
v = rho * v + dw
w -= learning_rate * v이 전의 gradient도 계속 더해주기 때문에 속력이 아닌 속도(velocity)로 표현 되었고 이전 gradient를 얼마나 고려할 것인지를 뜻하는(friction or decay rate) 수식에서의 p, 코드에서의 rho 값은 일반적으로 0.9를 사용한다고 한다.
현재 위치에서의 gradient에 velocity를 더해주는 형태인 momentum update를 간단한 벡터로 표현하면 다음과 같다.
SGD + momentum은 기존 SGD의 세가지 문제점을 해결하면서 훨씬 빠르게 동작한다.
이러한 개념을 언덕에서 공을 굴리는 것으로 비유를 들면 공이 점점 내려가면서 속도가 붙어 local minimum 혹은 saddle point를 만나더라고 velocity를 통해 탈출할 수 있다는 개념이다.
또한 위의 그림 처럼 이전의 poor condition문제(zigzag pattern)에서는 velocity vector가 경로를 좀더 smooth하게 만들어주는데 이는 quick oscillation이 일어나는 방향에서는 상대적으로 low velocity가 적용되고 horizontal direction 에서는 velocity가 accelerate되기 때문이다.
이런 momentum 방식을 좀더 개선시킨 알고리즘이 있는데 이를 nesterov momentum이라 부른다.
Nesterov Momentum
nesterov momentum는 직전에 봤던 momentum과는 약간 다른 방식으로 update가 이루어진다.
위 그림처럼 기존의 momentum이 현재 point에서의 gradient와 이전 velocity를 더해주어 update를 하는 반면에 nesterov momentum은 현재의 point를 이전의 velocity 방향으로 움직인 후 옮겨진 point에서의 gradient를 구하여 update시켜주는 방식이다.
수식과 코드로 표현하면 아래와같다.
v = 0
for t in range(num_steps):
old_v = v
v = rho * v - learning_rate * compute_gradient(w)
w -= rho * old_v - (1 + rho) * v
위 그림은 세가지 optimizer algorithm이 loss contour plot에서 이동하는 경로를 나타낸다.
그림에서 처럼 SGD+Momentum 과 Nesterov momentum은 bottom에서 overshoot 되는 경향을 보인다 (velocity를 사용했기 때문에).
이러한 momentum method들은 linear model 뿐만 아니라 많은 deep learning model 을 학습시킬때 흔하게 사용한다고한다.
* 강의에서 말하기를 사실 nestrov momentum은 objective function의 api에 잘 fitting되지 않으며, 신경망과 같은 convex function에서는 효과가 그렇게 좋은지는 모르겠다고 한다.
방금 보았던 것 처럼 SGD+momentum 과 Nesterov momentum은 bottom에서 oversoot되는 경향을 보인다. 이러한 문제를 극복하기위한 algorithm이 등장하였다.
Adagrad
우리가 가끔 접할 수 있는 또 다른 optimization function으로 (adaptive learning rates) Adagrad algorithm이 있다. 이것을통해 이전의 learning rate가 일괄적으로 적용되고 있어 overshooting 되었던 문제를 learning rate를 가변적으로 적용하여 해결하고자 한다.
historical average of gradient values(이 전의 velocity) 대신에 historical average of squares of gradient values를 keep tracking해 주는 형태이다.
* 말로는 이해하기 힘드니 코드를 통해 살펴보자.
grad_squared = 0
for t in range(nun_steps) :
dw = compute_gradient(w)
grad_squared += dw * dw
w -= learning_rate * dw / (grad_squared.sqrt() + 1e-7)현재 point에서 gradient를 계산하고 이를 element-wise 제곱한 값을 grad_squared 에 누적한다 (grad_squared는 gradient history라고 볼 수 있다). 이후 learning_rate를 grad_squared의 제곱근으로 나눠주어 step마다 learning rate를 가변적으로 적용하여 w를 update해주는 방식이다.
이를 통해 이전에 본 SGD 문제들 중 zigzag pattner(poor condition)에서 one direction에서 매우 빠르게 gradient가 변화하는 경우는 grad_squared.sqrt()값인 rarge value를 gradient에 나눠주는 형태가 되므로 진행을 약화시키고, 또한 gradient가 매우 느리게 변화하는 direction의 경우엔 grad_squared.sqrt()값인 small value를 나눠주어 accelerating motion 효과를 준다.
이러한 adagrad algorithm의 성질은 minima에 가까워질 수록 느려지기 때문에 convex function에는 좋으나 non-convex한 경우에는 saddle point에 갇힐 수 있다. 또한 adagrad를 매우 오랜시간 가동시킬 경우 step을 진행할 수록 grad_squared가 계속해서 누산되기 때문에 점점더 큰 값을 gradient에 나누어주게되고 step을 진행할 수록 learning rate를 감쇠시키는 역할을하여 bottom에 도착하기 전에 어딘가에서 결국 progress가 멈추게되는 효과를 보인다.
이러한 문제를 극복하기 위해 adagrad를 직접적으로 사용하지 않고 또다른 optimization algoritm인 RMS Prop과 같이 사용하여 adagrad의 leaky version으로 사용한다.
RMSProp
SGD+momentum 에서 friction coefficient (rho 혹은 p)가 매 iteration마다 velocity를 감쇠시키는 역할을 하는 것 처럼 adagrad 에서 average of squeare gradient에 일종의 friction을 추가시킴으로서 위의 문제를 극복한다.
* 코드를 통해 살펴보자
grad_squared = 0
for t in range(nun_steps) :
dw = compute_gradient(w)
grad_squared += decay_rate * grad_squared + (1 - decay_rate) * dw * dw
w -= learning_rate * dw / (grad_squared.squr() + 1e-7)위의 adagrad의 grad_squared 에 decay_rate 을 두어 기존에는 그대로 누적되던 것들을 조금씩 decay하게 만든다.
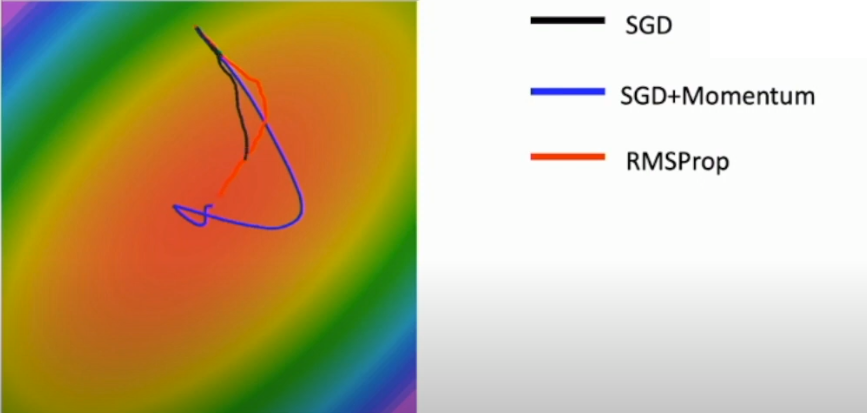
또 다시 heat map에서 볼 수 있듯이 RMSProp 는 momentum의 overshooting 문제를 극복한 모습이다.
이제 위에서 보았던 두개의 idea를 합친 더 좋은 algorithm을 살펴보려 한다.
Adam
이름에서도 유추할 수 있듯이 Adam 은 Adagrad(RMSProp) 와 Momentum을 합친 개념이다.
코드를 통해 이를 살펴보자
moment1 = 0
moment2 = 0
for t in range(num_steps):
dw = compute_gradient(w)
moment1 = beta1 * moment1 + (1 - beta1) * dw # momentum
moment2 = beta2 * moment2 + (1 - beta2) * dw * dw # AdaGrad / RMSProp
w -= learning_rate * moment1 / (moment2.sqrt() + 1e-7)
# beta1 & beta2 : each hyperparameter 위 코드에서 보다시피 이전의 momentum과 RMSProp를 적당히 섞어놓았다.
하지만 이러한 코드에서는 약간의 미묘한 문제가 발생한다.
t가 0일때 (시작지점에서) friction coeffitient인 beta2가 0.999가량의 매우 큰 값을 갖게 된다. 이것은 우리가 moment2를 0로 initialize 하였는데 first gradient step에서 moment2는 0에 매우 근접한 값을 갖게되어 moment2를 square root 취하었을때 0에 근접한 값을 갖게하여 결국 시작 step에서 매우큰 gradient step을 갖게된다 이것은 때때로 매우 나쁜 결과로 이끌 수 있다.
* 해당 내용의 자세한 내용은 링크의 논문에서 볼 수 있다
ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION
위와같은 문제를 극복하기위해 앞의 코드에 bias correction을 추가시켜준다. 코드는 아래와 같다.
moment1 = 0
moment2 = 0
for t in range(num_steps):
dw = compute_gradient(w)
moment1 = beta1 * moment1 + (1 - beta1) * dw # momentum
moment2 = beta2 * moment2 + (1 - beta2) * dw * dw # AdaGrad / RMSProp
moment1_unbias = moment1 / (1 - beta1 ** t)
moment2_unbias = moment2 / (1 - beta2 ** t)
w -= learning_rate * moment1_unbias / (moment2_unbias.sqrt() + 1e-7)
# beta1 & beta2 : hyperparameter for each moment Adam은 deep learning 에서 굉장히 좋고 자주 사용하는 optimizer라고 하고 hyperparmeter는 다음과 같이 사용하면 좋다고한다.
*
beta1 = 0.9
beta2 = 0.999
learning_rate = 1e-3 or 5e-4
Summery
-
이전에 보았던 regularization이 추가된 loss function을 가지고 weights를 update해나가는 optimization 방법론에 대해 살펴보며 기본적인 gradient descent의 동작 메커니즘에 대하여 살펴보았다.
-
Gradient algorithm 부터 시작하여 local minima, poor condition, saddle point 등 여러 발생할 수 있는 문제들을 새로운 optimization algorithm을 통해 극복해 나가는 모습을 살펴보았다.
-
다음 강의에서는 Neural Networks에 대한 기본적인 intro를 살펴보려한다.
