
Intro...
우리는 이 전까지 linear model을 parametic classifier로 설계하면서 몇 개의 loss function을 다루어보았고 gradient descent 기반 algorithm에서 접할 수 있는 여러 문제들을 극복하기위한 여러 optimiaztion 방법 들에 대하여 살펴보았다.
여태까지 다루어왔던 linear classifier는 비록 이해하기는 쉬울지라도 기능적인 부분에서 꽤 제한적이고 우리가 원하는 만큼의 성능을 보이지 못한다.
Linear classifier's problem
lec3에서 다룬 것 처럼 geometric viewpoint 로 보면 linear classifier는 high dimensional hyperplanes 그린 후 두 덩어리의 euclidean space로 분할한다.
하지만 아래의 그림과같은 경우엔 linear classifier가 두개의 색을 분류할 수없다.
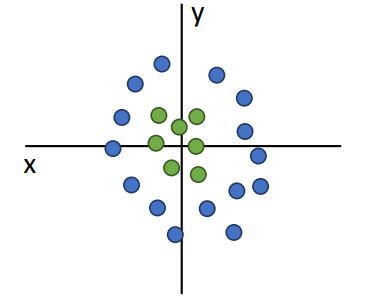
neural network를 접하기 전에 linear classifier의 이러한 문제들을 극복하는 방법들에대해 살펴보자.
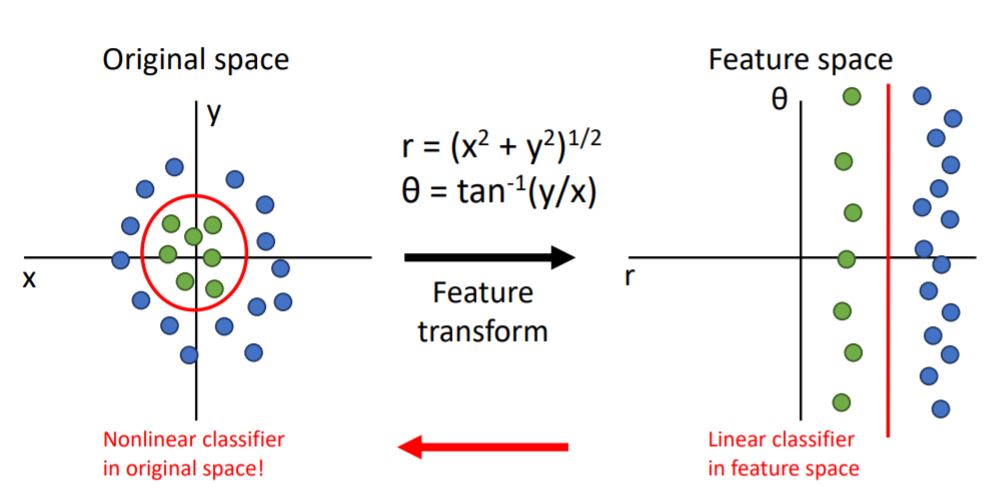
위의 그림처럼 우리는 data를 cartesian coordinate(데카르트 좌표계) 에서 polar coordinate(극 좌표계)로 변형시키면 좀더 수월하게 classification할 수 있게된다.
이러한 feature space에서 data set은 linearly separable 하게되고 linear classifier는 linear decision boundary에서 classification이 가능해진다.
1. Color Histogram
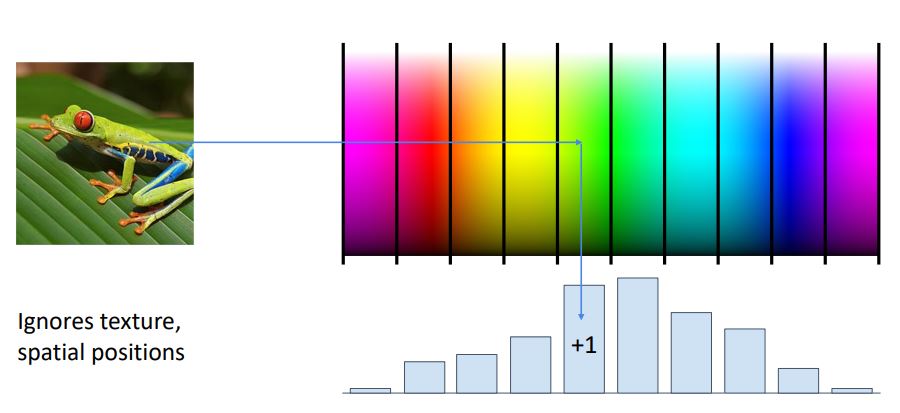
이미지의 rgb정보가 (혹은 hsv폼의 hue data) 나타내는 color 정보를 일정한 color별로 categorical 하게 분류하여 normalized histogram으로 변형시켜 해당 image에 어떠한 color들이 분포해있는지 나타낼 수 있다.
2. Histogram of Oriented Gradients (HoG)
이미지의 또다른 feature representation은 매우 널리 사용되는 HoG가있다.
Color histogram에서는 texture나 location을 고려하지 않은 color정보에 대해서만 표현한 방식이었다. HoG는 이와 반대로 color정보를 고려하지 않고 local edge의 방향 및 강도를 표현한다.
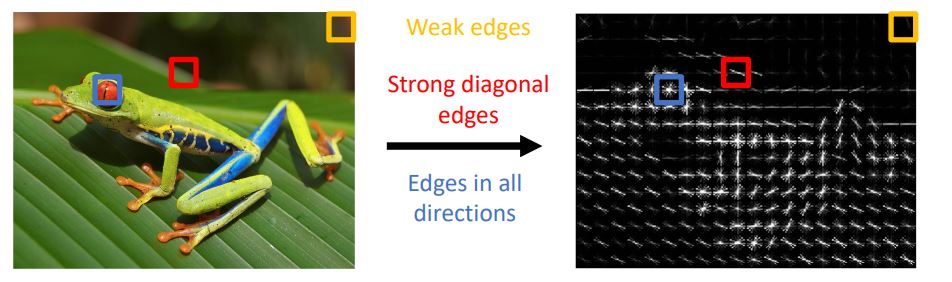
HoG를 visualize하면 위 그림과 같이 나타나는데 그림에서 빨간 박스의 영역은 강한 대각선 edge로 나타나고 파란 박스는 모든 다른 방향의 edge가 나타나는 것을 볼 수 있다.

BoG는 우리가 큰 이지지의 traing set을 가졌을때 다양한 scale과 size의 random patch set를 추출 하는 것이다. 그리고는 random patches를 군집화시켜 code book 혹은 visual words라 불리는 것을 만들고 이것은 어떤 종류의 feature가 우리의 이미지들에서 나타나는 경향이 있는지를 표현한다.
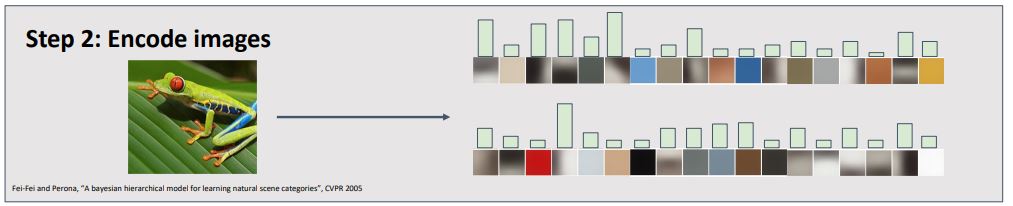
몇개의 feature representation을 살펴보았지만 우리는 하나만 골라서 쓸 필요는 없다.
4. Image Features
이전의 feature representation을 서로 연결시켜 한개의 high dimensional feature vector로 사용할 수 있다.
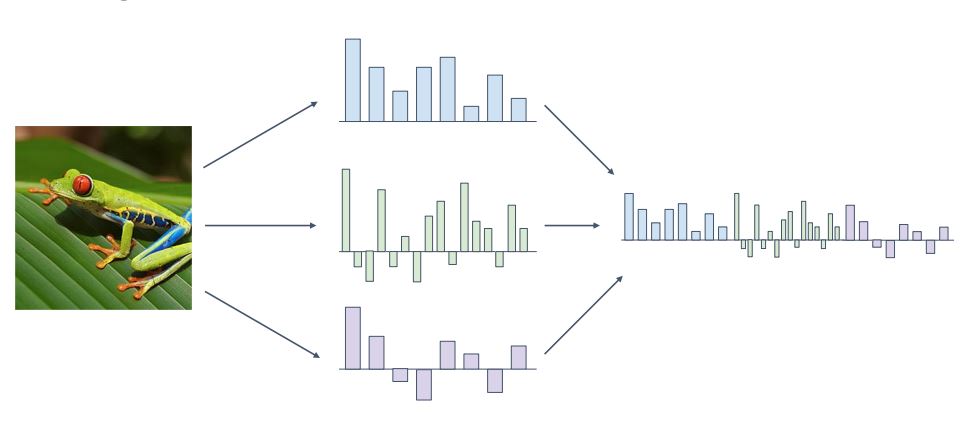
이렇게 몇 개의 feature representation을 조합하여 사용하는 것은 많이 사용해 왔다.
Image Features vs Neural Network
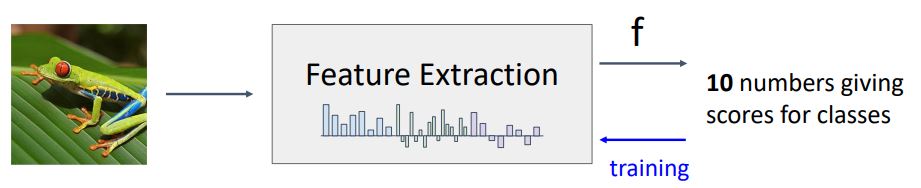
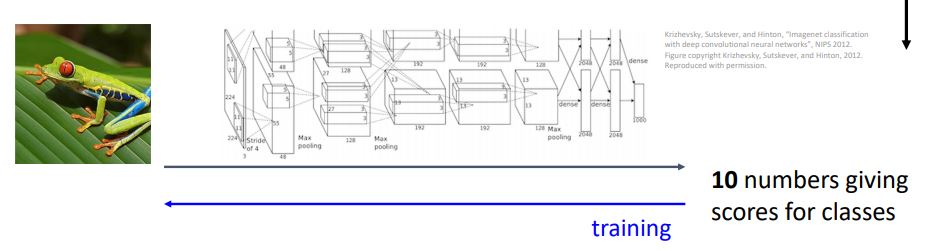
Neural Network
이제 살펴볼 가장 simple한 neural network model은 linear classifier 만큼 복잡하지 않다.
우선 수식을 통해 간단한 neural network model과linear classifier의 차이를 살펴보자.
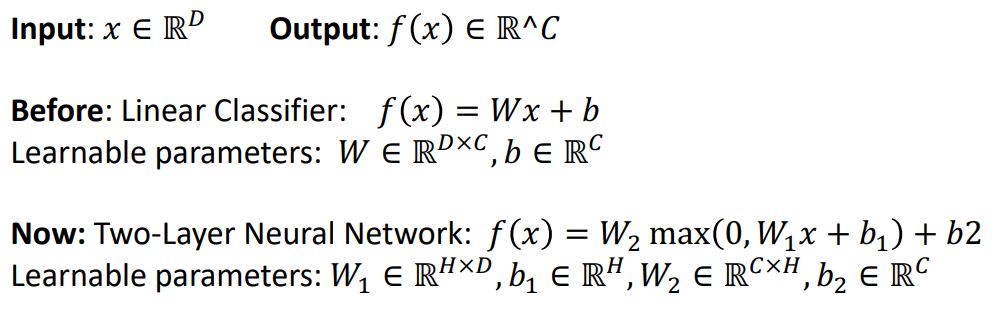
element-wise maximum function을 취하여 (c x h)의 size를 갖고있는 W2 와 곱해주게 된다 (이때 c는 num of ouput channels를 뜻한다)
위 수식은 2-layer Neural Network의 일반적인 형태를 나타내며 아래와 같은 형태로 neural network layer를 쌓아갈 수 있다.
f(x)=W3max(0,W2max(0,W1x+b1)+b2)+b3
이러한 형태의 시스템(2-layer Neural Network)을 아래와 같은 그림으로 표현할 수 있다.
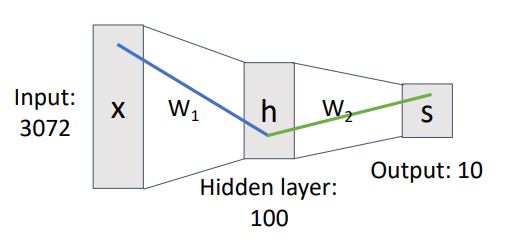
위 그림처럼 neural network에서는 왼쪽에서 오른쪽으로 data flow가 표현된다.
우리는 이 weight matrix(w1, w2)를 이전 layer의 element들이 다음 layer에 얼마나 영향을 미치는지 우리에게 알려주는 것으로 해석해볼 수 있다.
* 이 weight matrices는 dense general matrices라고 한다.
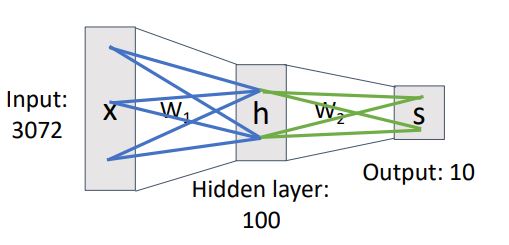
이러한 dense connectivity pattern 때문에 neural network를 일반적으로 Fully connected network라고 부른다. 또한 이러한 구조를 때때론 Multi-Layer Perceptron(MLP)라고도 한다
이제 이 Neural network가 정확히 무엇을 계산하고있는지 neural network based classifier와 Linear classifier를 비교하면서 살펴보자.

위의 그림처럼 이전 3강 내용중 linear classifier가 클래스별 하나의 template만을 갖고있었던 것을 상기시켜보면 여러 문제점들이 있었던것을 떠올릴 수 있을 것이다.

Neural network의 첫번째 weight matrix인 w1이 linear classifier의 template과 매우 비슷한 형태이지만 우리가 정한 hidden layer의 크기에 맞는 W1의 크기 만큼 template을 가진다는것이 큰 차이이다.
위의 이미지에서 나타나는 template들은 대부분 무엇을 뜻하는지 해석이 불가능하다.

우리가 몇안되게 식별할수있는 형태의 template을 통해 살펴보면 red box부분 template중 하나는 말의 머리가 왼쪽으로 향한 형태의 template이고 다른 하나는 머리가 오른쪽으로 향한 template이다.
second-layer를 통해 이러한 여러 형태의 template을 recombine시키고 그때의 weight matrix인 w2는 다른 형태의 template들을 모두 cover하는 형태가 되므로 이전의 linear classifier 에서 나타났던 two-headed horse 문제를 극복 할 수 있게된다. 이러한 형태를 때때로 distributed representation 이라고 표현한다.
앞에서 보았던 2-layer neural network system을 확장시켜 살펴보면 아래의 그림처럼 나타낼 수 있다.
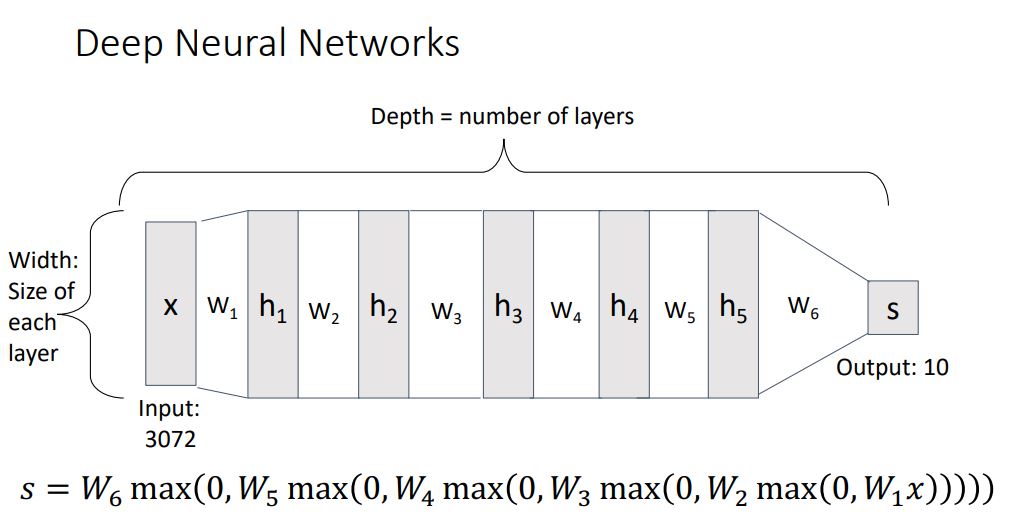
Activation Function
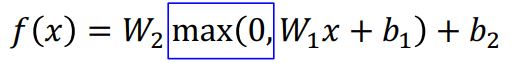
위 그림에서 우리가 이전에 보았던 파란 박스로 나타낸 max함수와 같은 것들을 activation function이라고 한다.

이러한 function은 위의 그래프 처럼 argument가 positive값을 가지면 그대로 return 해주고 negative값을 가지면 0을 return해주는 형태의 함수로 우리는 이것을 ReLU (Rectified Linear Unit)이라고 한다.
이러한 activation function들을 neural network에서 두개의 다른 weight matrix사이에 낀 형태로 생각해 볼 수있다.
Q) 만약 우리가 activation function 없이 neural network를 구성한다면 어떻게 될까??
f(x)=W2(W1x+b1)+b2=(W1W2)x+(W2b1+b+2)
위 수식처럼 이러한 형태는 여전히 linear classifer의 형태이다. 그렇기에 neaural network에서 어떤 activation function을 선택하는지는 매우 중요한 부분이다.
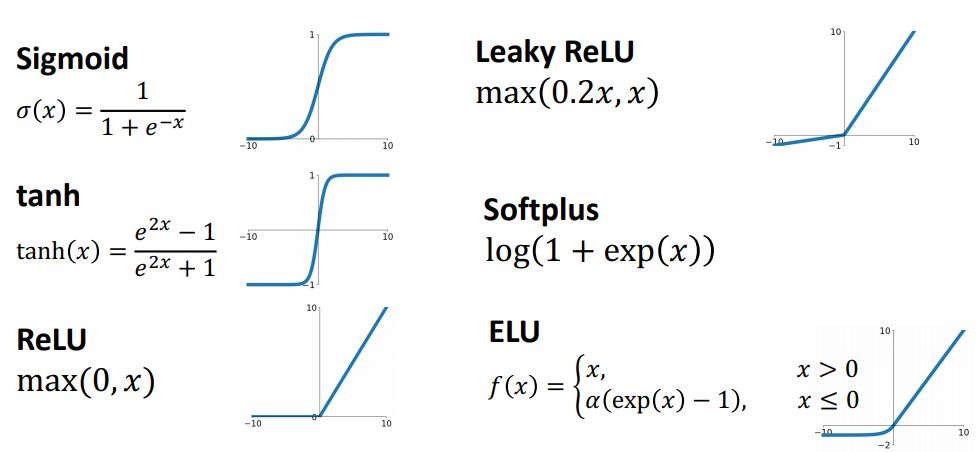
앞에서 본 ReLU activation function 외에도 아래의 그림에서 처럼 많은 activation function들이 있다.
앞에서 보았던 간단한 neural network system을 pytorch가 아닌 numpy를 사용하여 구현한 형태의 코드를 통해 살펴보자.
import numpy as np
from numpy.random import randn
N, Din, H, Dout = 64, 1000, 100, 10
x, y = randn(N, Din), randn(N, Dout)
w1, w2 = randn(Din, H), randn(h, Dout)
for t in range(10000):
h = 1.0 / (1.0 + np.exp(-x.dot(w1)))
y_pred = h.dot(w2)
loss = np.square(y_pred - y).sum()
dy_pred = 2.0 * (y_pred - y)
dw2 = h.T.dot(w2.T)
dh = dy_pred.dot(w2.T)
dw1 = x.T.dot(dh * h * (1 - h))
w1 -= 1e-4 * dw1
w2 -= 1e-4 * dw2
위의 코드는 다음과 같은 과정을 거쳐 설명된다
1. Initialize weights & data
2. Compute loss(using sigmid activation & L2 loss)
3. Compude gradients
4. SGD step
이러한 코드는 매우 간단하게 구현되었지만 위의 코드를 돌려보면 실제로 neural network가 학습하는 것을 볼 수 있게된다.
우리는 직전에 neural network를 image template의 예로 살펴보았는데 또다른 관점에서 Linear classifier와의 비교를 통해 왜 Neural network가 강력한지 살펴보자 .
Space Warping
3강에서 봤던것 처럼 geometric 관점에서 linear classifier는 data point가 high dimensional space에 있고 2개의 pixel에 대해 나타냈을때 아래의 그림에서 처럼 두개의 line은 해당 class의 score가 0임을 나타내고 line의 perpendicular plane이 해당 class의 score를 linear하게 나타낸다는 것을 보았었다.
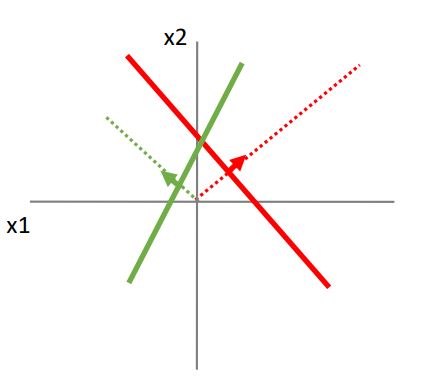
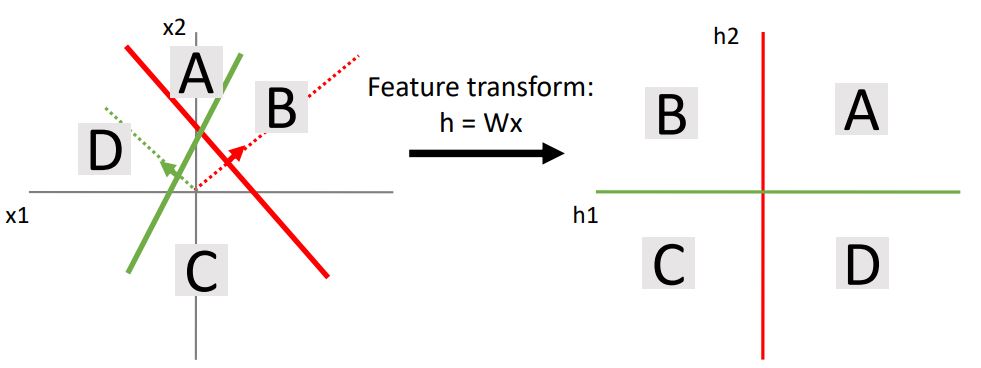
위의 region of space를 data point 관점에서 살펴보자.
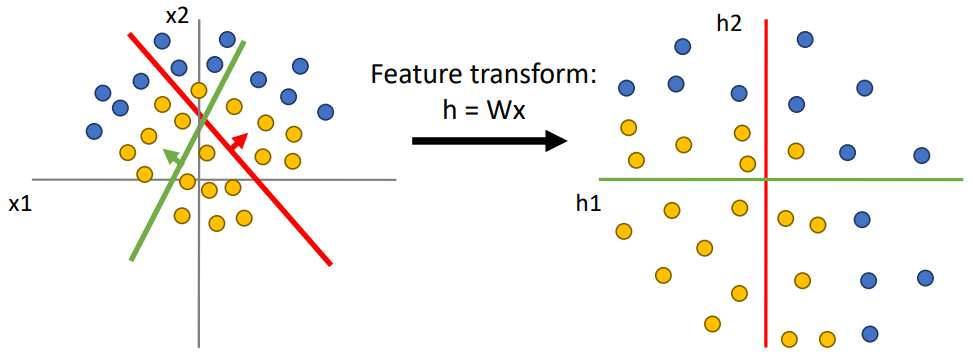
이제 ReLU function을 통해 space warping 시켜보면 region of space가 다음과 같이 나타나게 될 것이다.
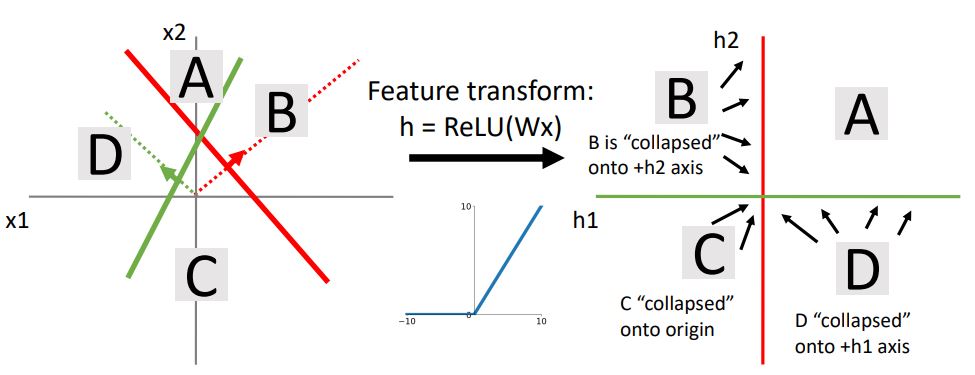
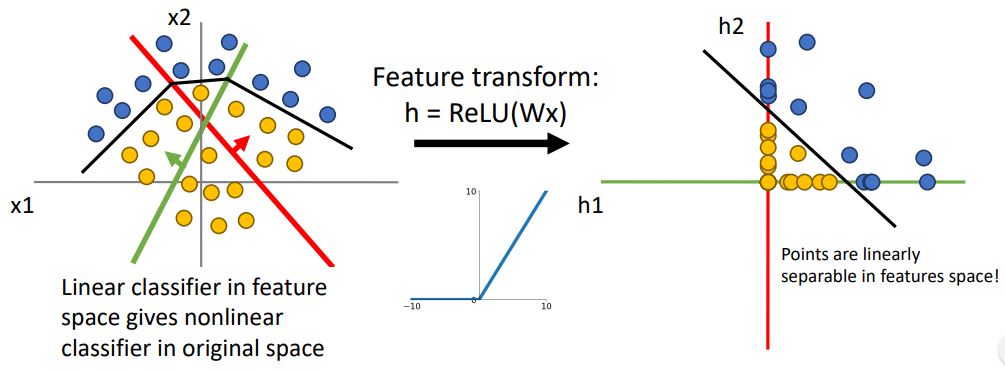
만약 hidden layer를 점점더 증시켰을때는 어떤 현상이 일아날까?
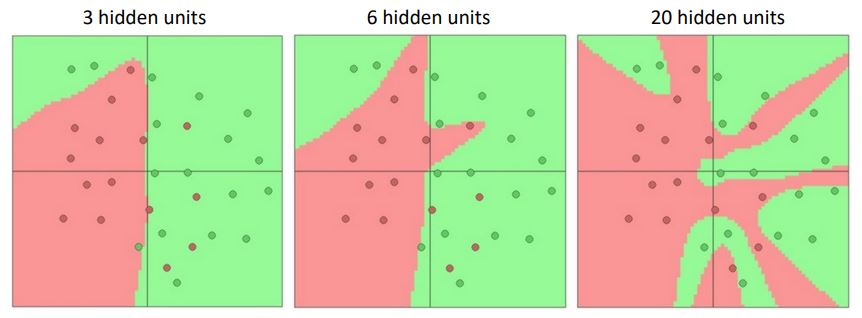
여기서 한가지 의문이 들 수도있다. 그림에서처럼 hidden layer가 증가할 수록 model은 overfitting되어 보인다. 하지만 overfitting을 줄이기 위해 hidden layer를 줄이는것은 좋은 regularization 방법이 아니다.
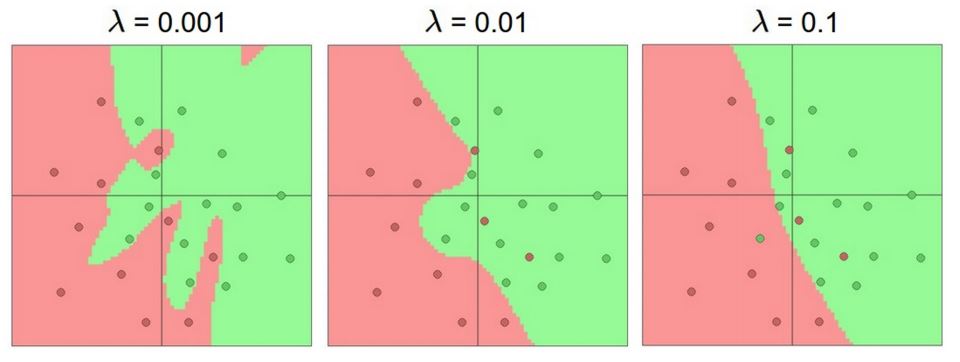
Neural network model 에서는 위 그림에서 L2를 사용한 것 처럼 몇가지 regularization parameter들을 사용한다.
이전까지 neural network가 linear classifier보다 훨씬 poweful 하다는 것을 보았는데 이것을 좀더 공식화 시켜보자.
Universal Approximation
(하나의) hidden layer를 가지고있는 neueal network system은
f:RN−>RM 형태의 어떤 함수로 근사하게 표현될 수 있다.
ReLU based neural network system이 대수적으로 output값을 어떻게 계산하는지 어떤 함수의 근사치를 계산함으로서 이를 살펴보자.
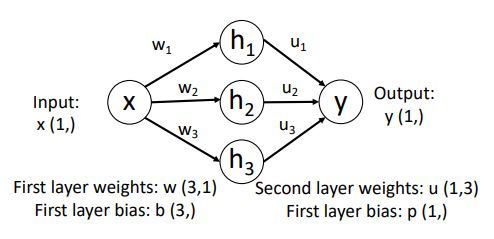
h1=max(0,w1∗x+b1)h2=max(0,w2∗x+b2)h3=max(0,w3∗x+b3)y=u1∗h1+u2∗h2+u3∗h3+p
output value인 y는 hidden layer value의 linear combination 형태로 나타나낼 수 있다.
이러한 output value를 또다른 형태로 나타내보자.
y=u1∗max(0,w1∗x+b1) +u2∗max(0,w2∗x+b2) +u3∗max(0,w3∗x+b3)+p
위처럼 y는 3개의 다른 terms들로 분해될 수 있으며 이 각각의 terms들은 ReLU function의 shifted or scaled or tlaslated된 버전으로 생각할 수 있다.
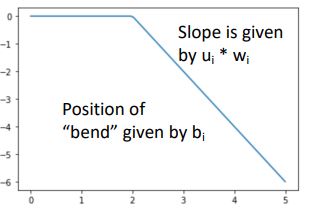
위의 그림은 위 수식의 각 terms를 ReLU의 shifted or scaled version으로 sign of w_i (w_i의 부호)에따라 왼쪽 혹은 오른쪽으로 flip될 것이며 bias만큼 shift되는 형태이다. 이때의 slope는 u_i * w_i 가 된다.
이러한 shifted or scaled version of ReLU를 통해 어떠한 function의 approximation을 만들 수 있다.
이러한 함수를 "bump function"이라고 한다.
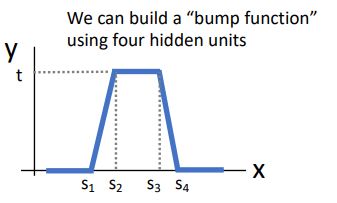
이러한 형태는 4개의 term(hidden unit)을 가진 linear combination으로 나타낼 수 있는데 (shifted or scaled version of ReLU 인 4개의 terms를 모두 더해주는 형태로) build up 되는 과정을 다음과 같은 그림으로 나타낼 수 있다.
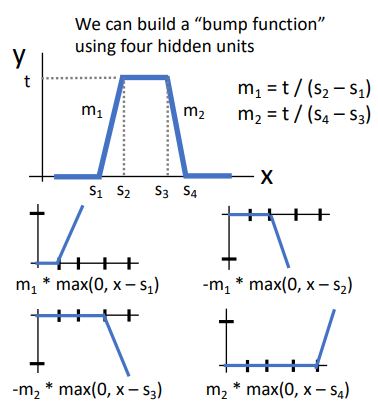
* 자세한 과정의 설명은 생략하겠다.
이 bump function은 4개의 hidden layer로 이루어졌지만 아래의 그림처럼 우리는 8, 12, 16...개의 hidden unit을 가진 neural network를 4-hidden unit bump function을 기준으로 K배 해준 모든 bumps 들을 더해주어 최종 함수를 build할 수 있게 된다.
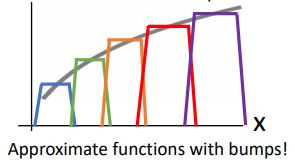
이렇게 우리는 어떠한 continuous function이든 approximate 할 수 있게된다. scale을 잘 조정하고 shift해주며 점점더 많은 hidden unit을 사용 할 수록 우리가 나타내고자 하는 continuous function에 근사 할 수 있게 된다.
하지만 실제로 neural network가 이러한 bump function을 학습하지는 않는다고 한다. 이것은 neural network의 principle을 설명하고자 할 때 수학적인 구조로써 사용된다. 또한 이것은 optimization이 어떻게 동작하는지 설명하지 못한다는 점이 있다.
Convex Function
function이 아래와같은 특정한 inequality constraint(부등호 제약조건)을 만족한다면 convex function이라고 말 할 수 있다.
A function f:X⊆RN−>R is convex if for all x1,X2∈X,t∈[0,1],f(tx1+(1−t)x2)≤tf(x1)+(1−t)f(x2)
쉬운 예로 x^2 함수를 통해 살펴보자.
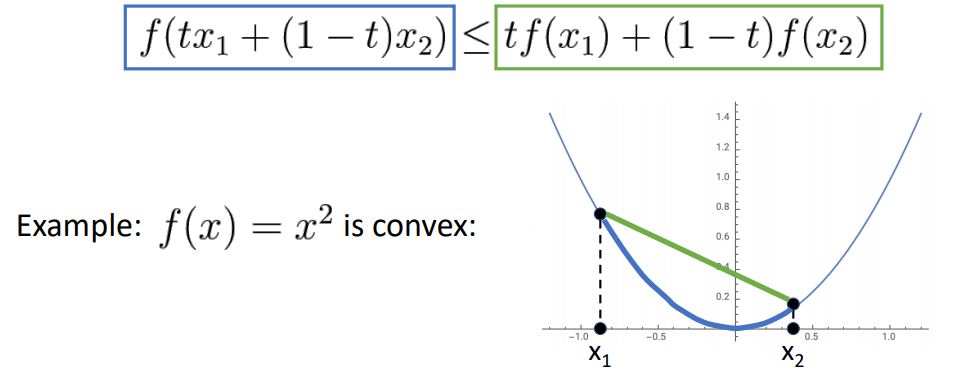
위 그림처럼 x^2 함수는 inequality constraint을 만족하기에 convex function이다.
또다른 예로 cos(x) 함수를 살펴보자.
%20is%20not%20convex.JPG)
위 그림에서 보듯이 cos(x)는 convex function이 아니다.
이러한 convexity를 좀더 일반적인 high-dimensional function으로 나타내면 다음과같은 bowl 모양의 함수로 나타난다.
.JPG)
우리가 이전까지 많은 시간을 들여 linear classifers에 대하여 살펴봤던 이유는 아래와같은 loss function들이 optimization을 위해 미분을 하면 convex function이 되어 global minimum에 도달하기 위한 theoretical guarantees를 제공하기 때문이다.

불행하게도 neural network system에 이러한 guarantees는 존재하지 않는다.
그렇기에 대부분의 neural network system 은 non-convex optimization이 필요하다
Summary
-
-
2. linear classifier와 2-layer neural network를 비교하여 살펴봄 으로써 왜 neural network가 powerful한지 살펴보았다.
-
3. space warping, universal appriximation, non-convex을 통해 neaural network system이 어떠한 특성을 갖는지 살펴보았다.

