[EECS 498-007 / 598-005] 6. Backpropagation

Intro.
지난 시간에 neural network는 categorical classifier에 매우 강력하다는 것을 살펴 보았다. 하지만 크고 복잡한 neural network system 에서는 어떻게 gradient를 계산할까?
우리가 이전에 보았던 loss fucntion을 미분하고 ∇WL을 구하여 gradient를 계산하는 방식은 neural network 와 같은 매우 복잡한 모델에서 실현 가능하지 못한다. 뿐만 아니라 모듈화 되어있지 않아 중간에 loss function을 바꿀수도 없다.
computer science 관점에서 data structure와 algorithms의 개념을 사용하여 위의 문제를 해결하여 gradient를 계산해보자.
Computational Graphs
Computational Graphs는 우리의 모델 안에서 행해지는 계산들을 그래프의 형태로 나타낸 것이다.
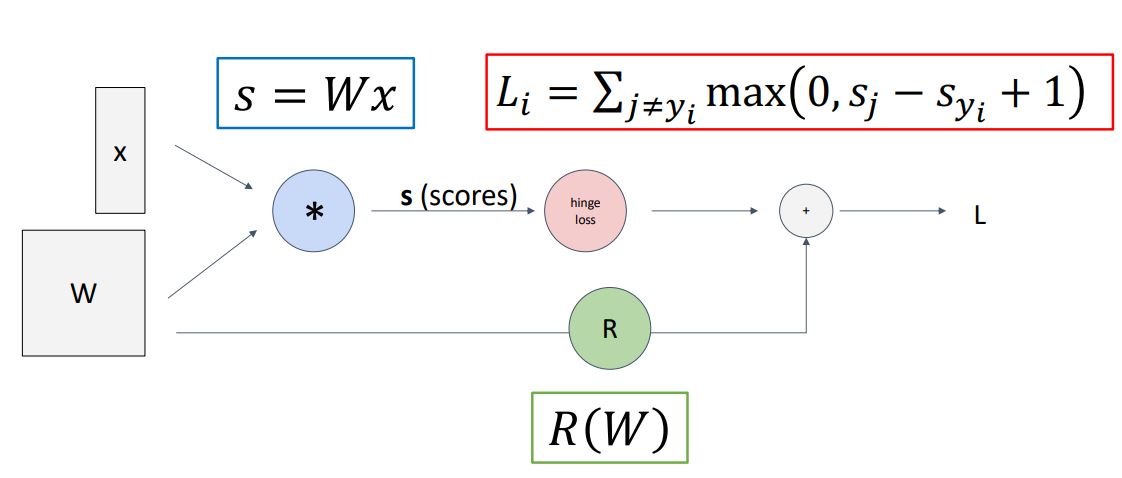
위의 그림은 이전에 보았던 linear classifier model의 loss를 계산하는 과정을 hypothesis function, loss function, regularization term 과정을 뜻하는 각 노드로 나누어 graph로 나타낸 것 이다.
앞의 computational graph는 linear classifier를 computational graph로 나타낸 형식적인 graph 이지만 모델이 점점더 커지고 복잡한 형태가 될 수록 이러한 방식은 중요하게 다가올 것이다.
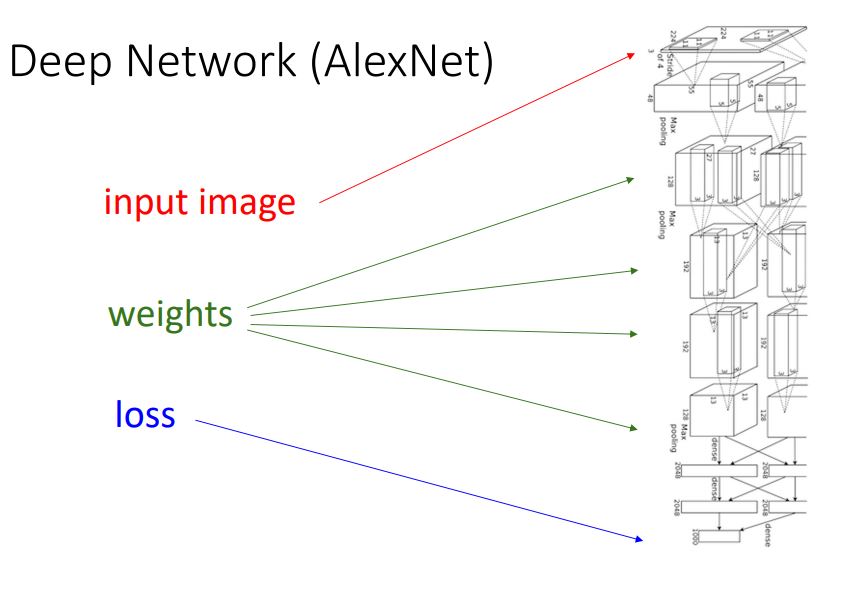
한 예로 위 그림이 나타내는 deep network인 AlexNet을 보면 많은 layer를 통해 model의 모든 계산과정이 computational graph를 통해 구조화 되고 형식화 되어 있다는 것을 볼 수 있다.
간단한 funtion을 통해 이러한 computational graph를 나타내보고 backpropagation 이라는 과정을 통해 gradient를 계산해 나가는 과정을 살펴보자.
* backpropagation이란 computational graph에서 gradient를 계산하기 위한 algorithm을 말한다.
Backprop simple example
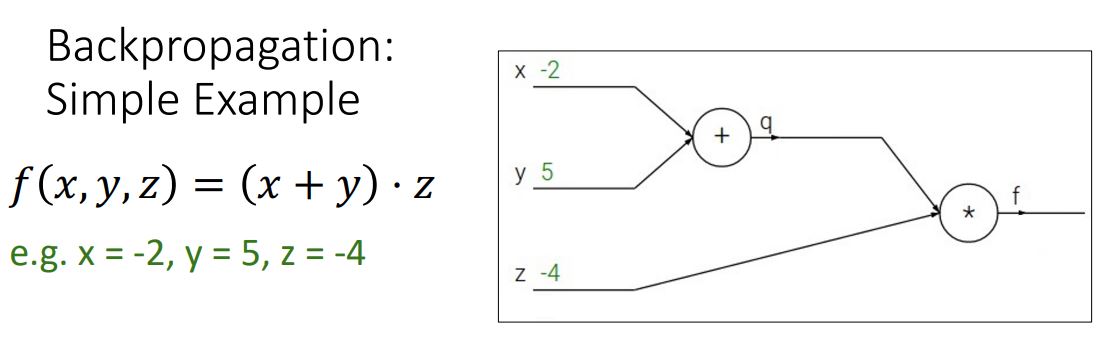
위 예시와같은 간단함 함수를 computational graph로 나타내고 backpropagation을 통해 gradient를 계산해보자.
1. Forward pass : compute output
: 주어진 input값으로 computational graph의 모든 노드를 계산하고 output을 계산한다.
q=x+y, f=q∗z
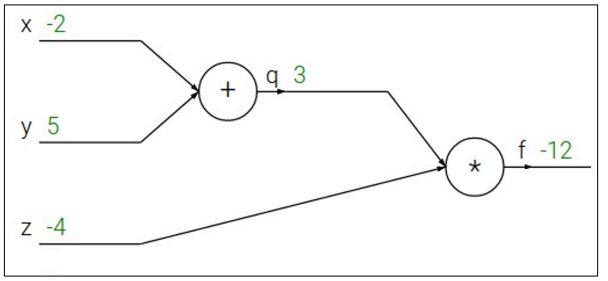
2. Backward pass: Compute derivatives
: output쪽의 노드부터 전체 function인 f를 각 노드가 나타내는 함수로 편미분하여 upstream gradient를 만들고, chain rule을 적용시켜 local gradient(현재 노드의 gradient)를 upstream gradient과 곱해주어 상위 노드의 gradient를 계산하는 과정으로. 처음 input단의 gradient를 계산해 나가는 방식이다.
2_1. compute local gradient
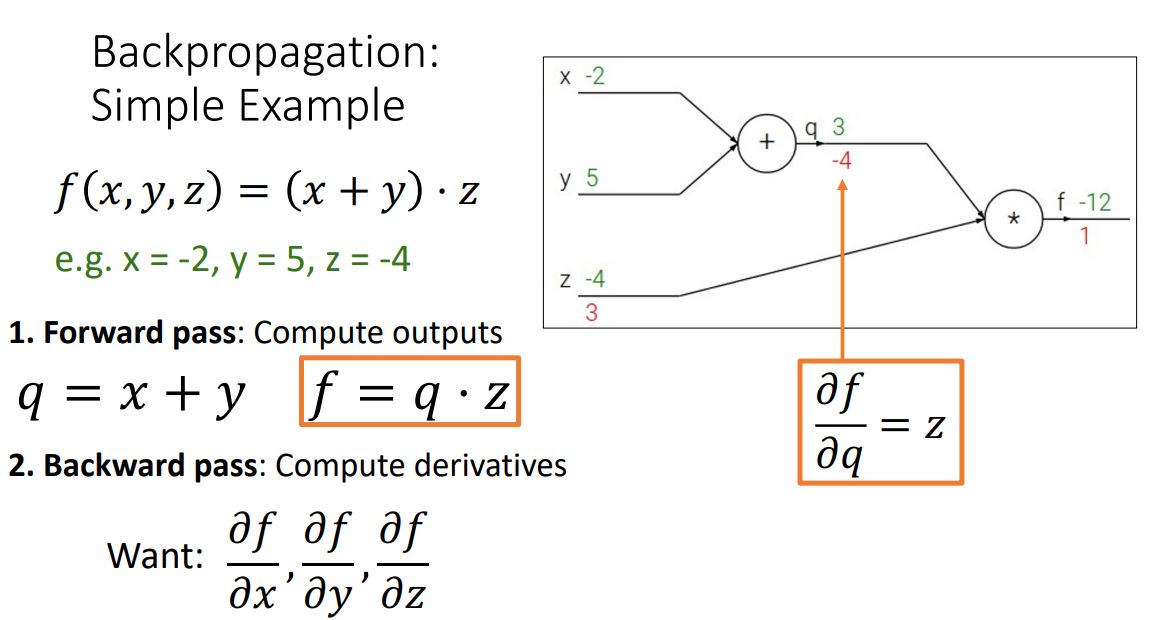
2_2. compute downstream gradient
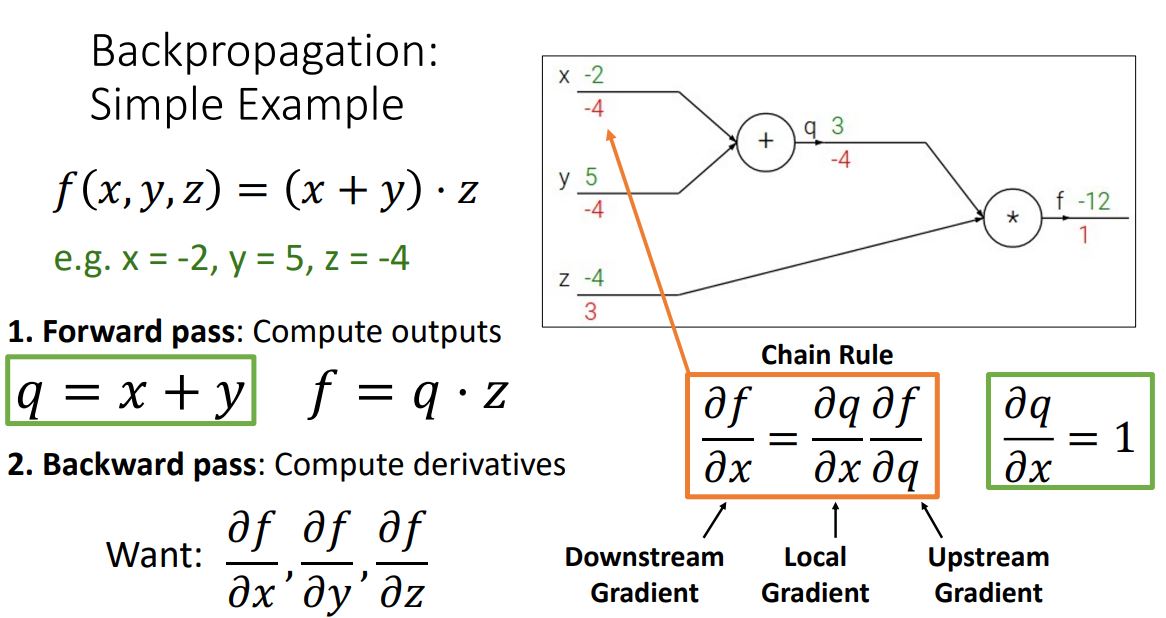
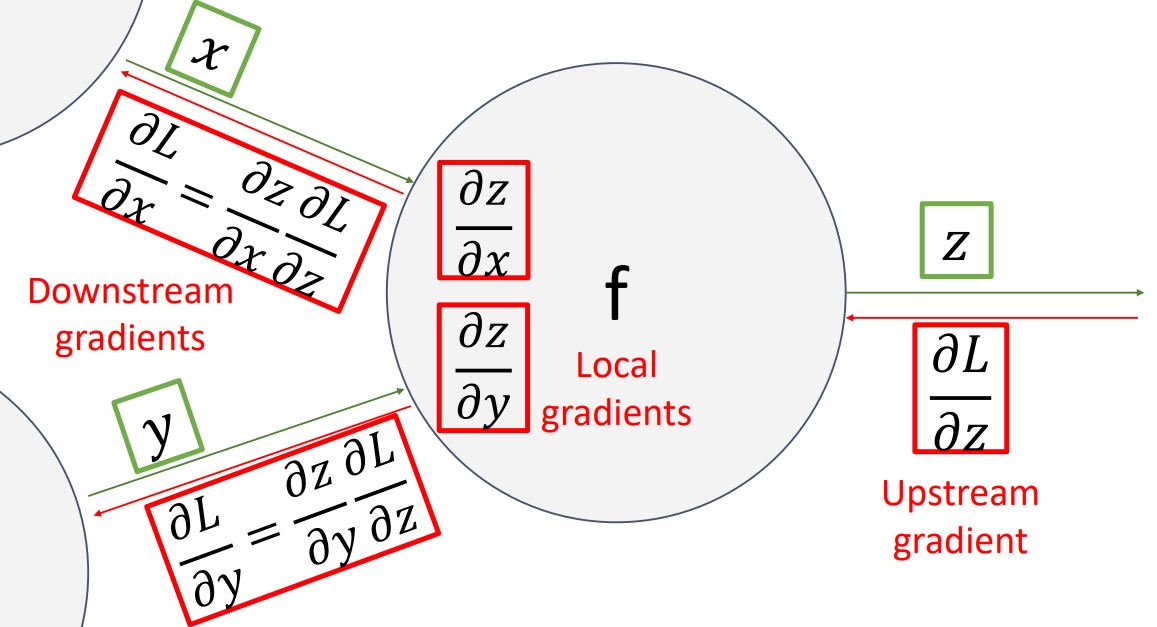
이러한 backpropagation 과정을 하나의 노드(혹은 전체 function) 관점에서 나타내면 다음 그림과 같다.
Another exmaple
또 다른 예로 logistic classifier의 형태의 함수를 computational graph로 나타내고 backpropagation을 통해 gradient를 계산해보자.
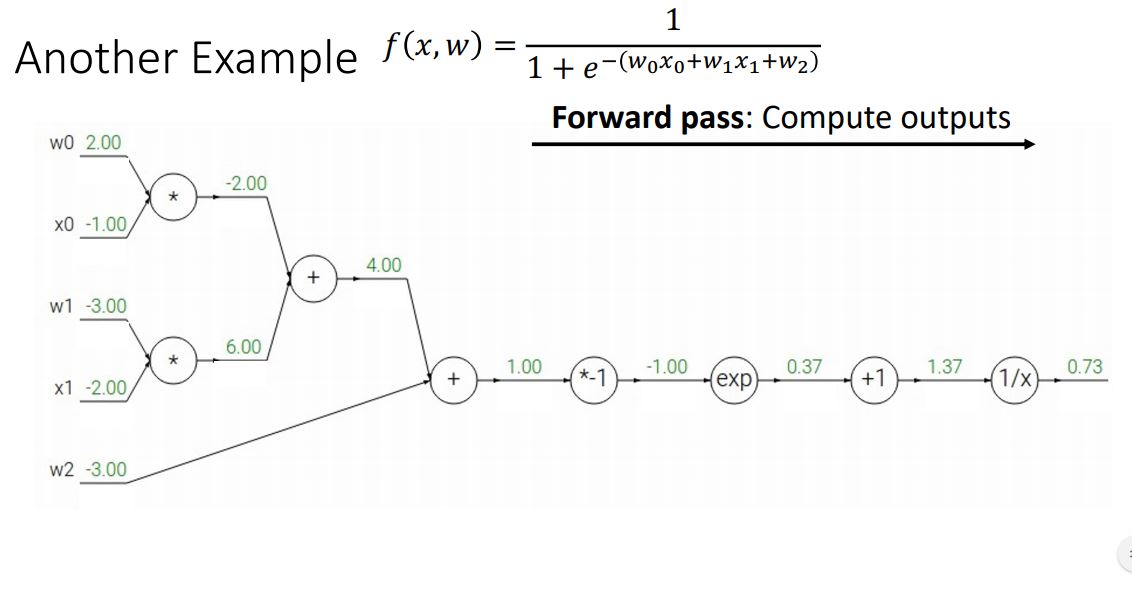
우선 위 그림처럼 logistic classifier의 형태의 함수를 computational graph로 나타내고 forward pass과정을 통해 ouput을 계산한다.
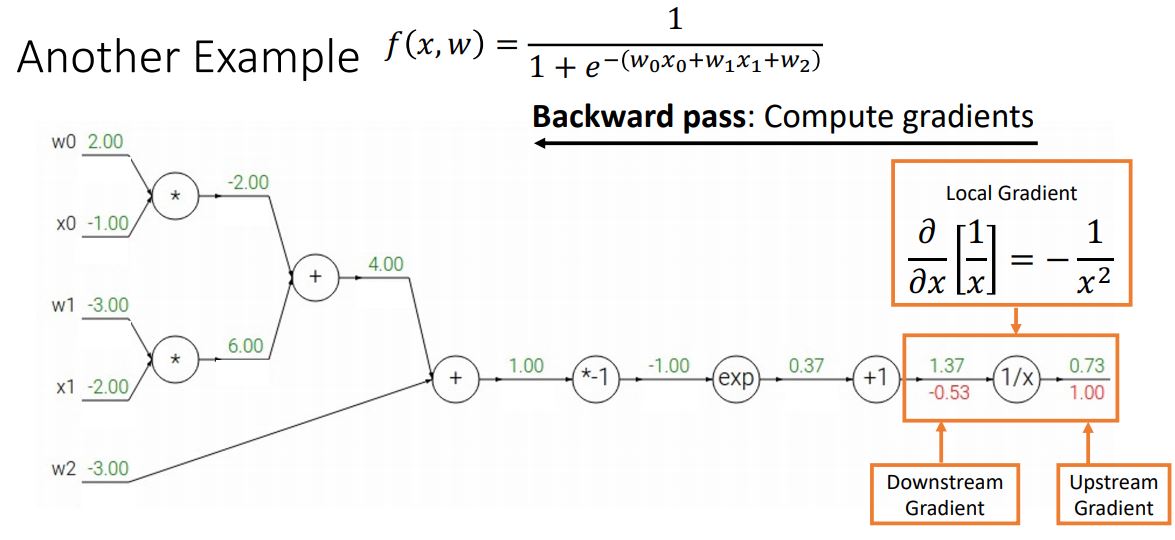
backward pass의 첫번째 노드에서 downstream gradient를 계산하는 과정이다.
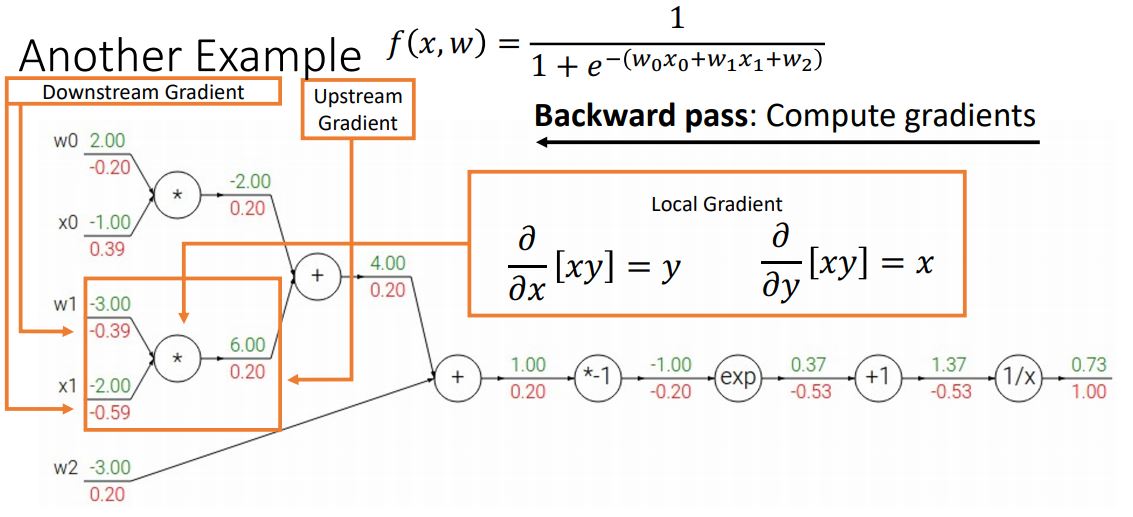
computational graph는 모든 primitive operation, fundmental operation(+, *, exp 등등)을 펼처놓는 형태여야만 하지 않고 다양한 structure로 표현 될 수 있다.
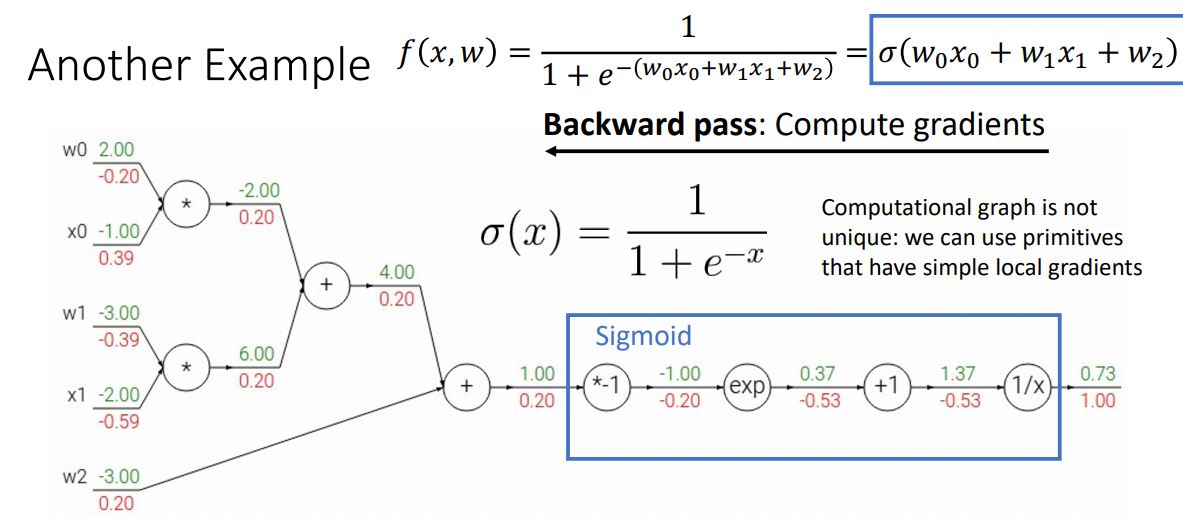
위의 computational graph에서처럼 우리는 primitive function을 사용하여 몇개의 노드를 하나로 묶어서 사용 할 수 있다.
* 위 그림에서는 primitive function인 sigmoid function을 활용하고있다.
* 추가로 sigmoid function이 자주 사용되는 이유는 sigmoid function의 local gradient를 계산할때 sigmoid function을 미분한 형태가 매우 간단하게 표현된다는 점 때문이다.
이렇게 primitive function을 사용하면 좀더 쉽고 간편하게 backpropagation과정을 계산할 수 있게 된다.
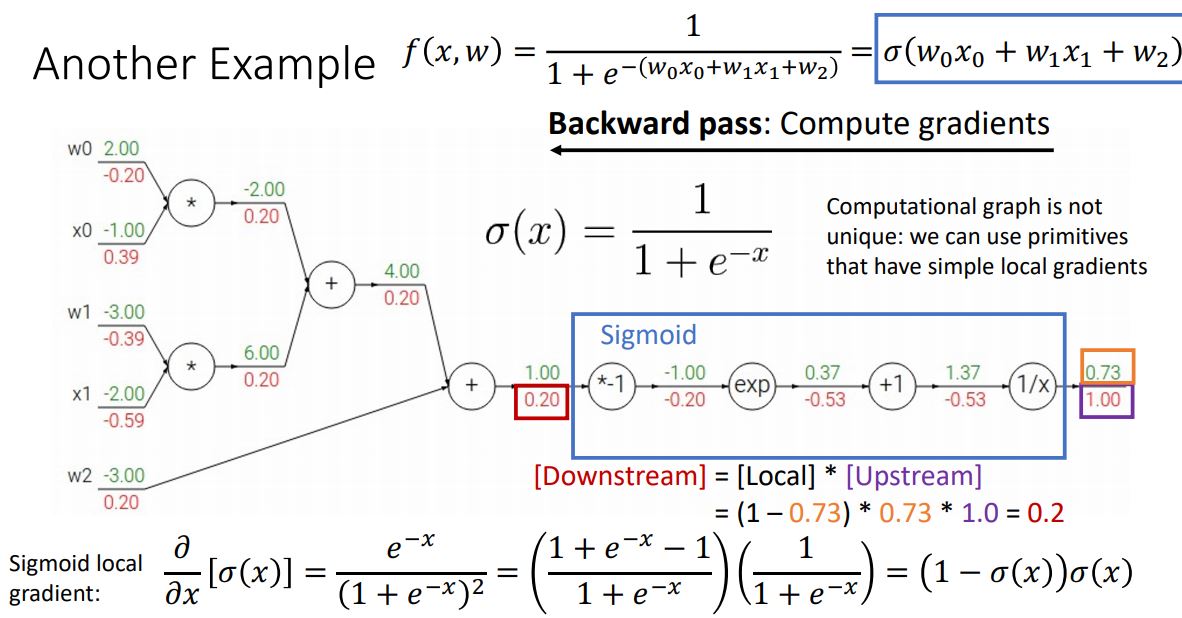
위 그림은 sigmoid function을 통해 좀더 간편하고 효율적으로 gradient를 계산하는 것을 보여준다.
Patterns in backprop
computational graph를 일종의 circuit으로 생각하여 특정 gate의 backward pass에서의 역할이라 생각해보면 편하다.
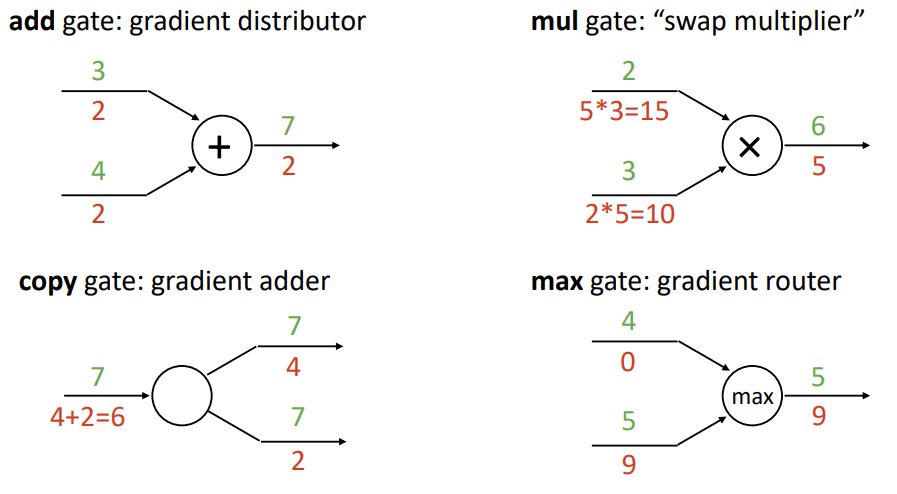
add function(add gate) : gradient distributor 역할
mul function(mul gate): swap multiplier 역할
copy function(copy gate) : gradient adder 역할
max function (max gate): gradient router 역할
Backprop Implementation with code
flat한 single python function으로 표현한 간단한 형태의 코드를 통해 이전에 보았던 computational graph의 backpropagation implementation을 살펴보자.
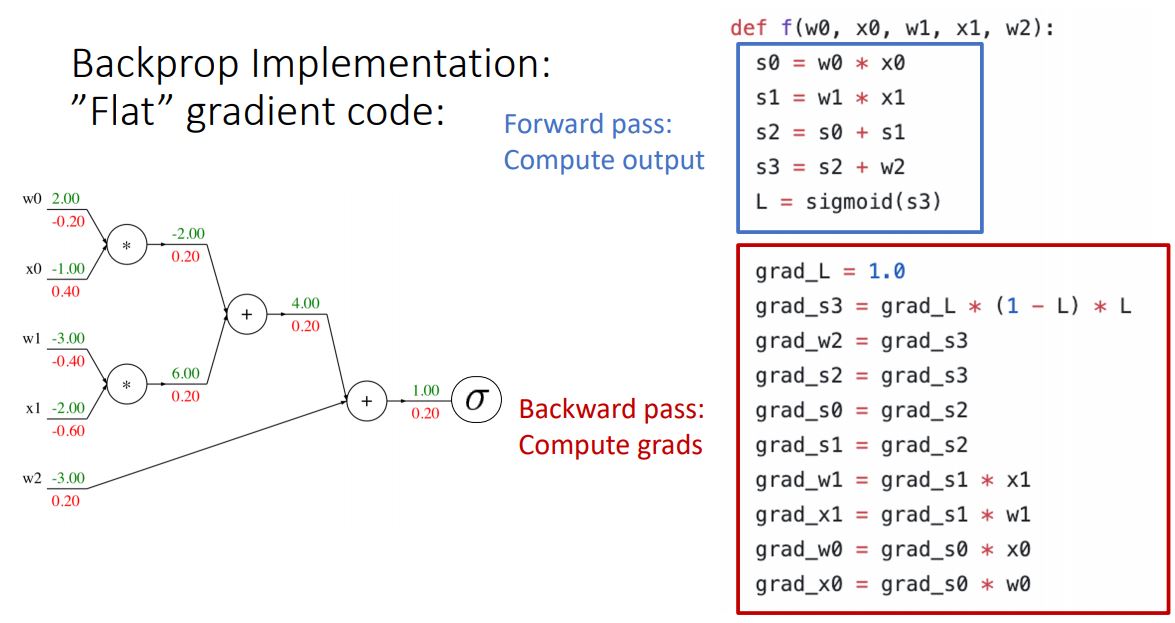
* 위 코드는 정말 간단한 코드라 내용에 포함시켜야할지 고민했지만 다시 코드를 통해 흐름을 보면 좋을 것 같아 포함시켰다.
위 코드는 forward pass 과정으로 computational graph의 각노드를 변수로 갖으며 flat한 계산흐름으로 output을 계산한 후 각 노드의 값들을 토대로 gradient를 계산해 나가며 backward pass를 표현한 코드이다.
이번엔 computational graph의 한 노드를 PyTorch를 통해 설계하는 간단한 코드를 살펴보자.

backward function에서는 upstream gradient를 파라미터로 받아 ctx tesor에서 가져온 local gradient인 x,y 값에 곱해주어 downstream gradient를 계산해주는 과정의 함수이다.
* 강의에서는 ctx를 arbitrary bits of information 을 저장하기 위한 context object라고 하는데 정확히 무슨의미인지는 모르겠다.
PyTorch는 기본적으로 auto grad engine으로 위와같은 형태의 operator들이 많이 구현되어있다.
실질적으로 sigmoid layer가 pytorch에 c++로 어떻게 구현되어있는지 살펴보자.

위의 코드를 자세하게 리뷰해볼 필요는 없지만 위의 코드를 통해 기본적으로 PyTorch는 forward, backward function을 쌍으로 갖는 layer(operator)들을 통해 big computational graphs를 설계하는 것으로 생각해 볼 수 있다.
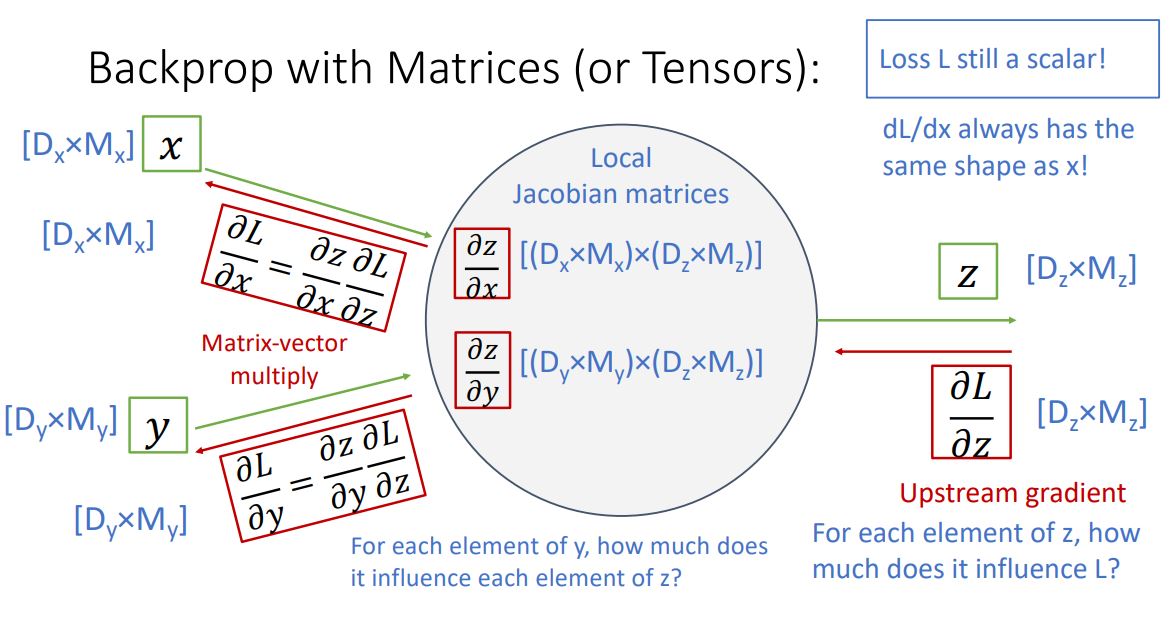
Backprop with Vectors
vector-valued function의 backprop을 살펴보기 전에 3가지 형태의 multivariable derivative에 대해 집고 넘어가자.
x∈R, y∈R:∂x∂y∈R
x∈RN, y∈R:∂x∂y∈RN
x∈RN, y∈RM:∂x∂y∈RN×M
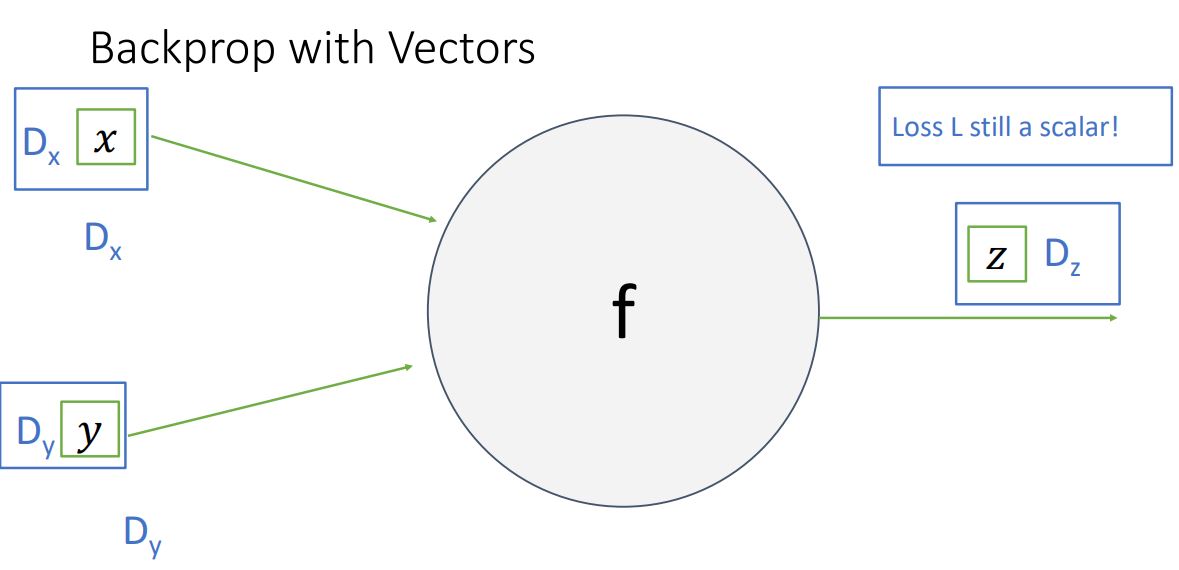
* 이때 중요한 것은 output은 vector이지만 loss는 언제나 scalar라는 것 이다.
.JPG)
upstream gradient인 ∂z∂L 는 scalar인 loss를 vector인 z로 편미분한 형태이기에 derivative는 gradient인 z-dim vector가 된다 (위의 2번 from). 이는 z vector에 각 element가 얼마나 loss에 영향을 미치는가를 나타낸다.
.JPG)
local gradient인 ∂x∂z 와 ∂y∂z 는 각각 z-dim vector를 x-dim, y-dim vector로 편미분한 형태이기에 derivative는 각각 x by z matrix, y by z matrix인 jacobian matrix가 된다(위의 3번 from).
.JPG)
마지막으로 downstream gradient인 ∂x∂L 와 ∂y∂L 는 chain rule을 통해 각각 해당하는 local gradient와 upstream gradient를 곱해주어 계산 할 수 있다. 이는 x gradient만 본다면 ∂x∂L=∂x∂z∗∂z∂L로 x by z matrix와 z-dim vector의 matrix multiply 형태이므로 x-dim vector가 나오게 된다.
또 다른 예로 ReLU function의 vector backpropagation과정을 살펴보자.
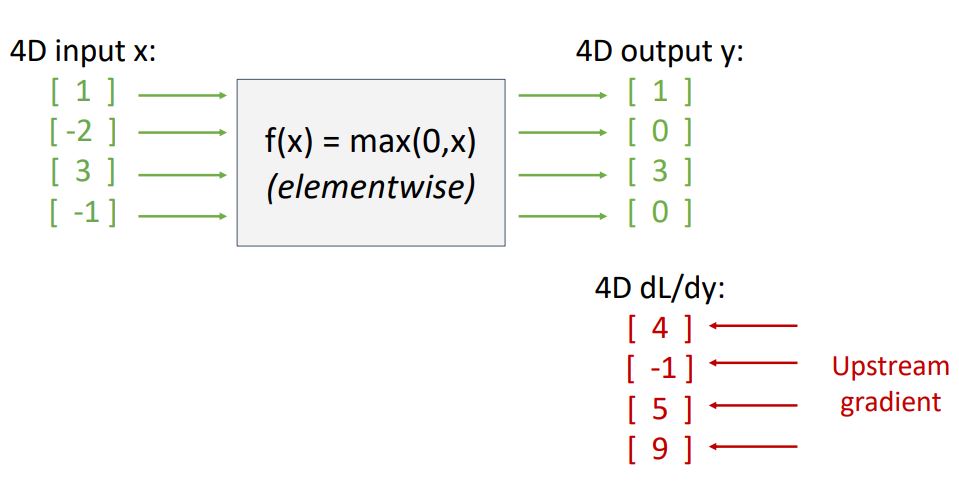
.JPG)
위 그림처럼 downstream gradient를 구하기위해 local gradient인 ReLU의 x에 대한 도함수 dy/dx matrix(jacobian matrix)와 upstream gradient dL/dy를 곱해준다.
하지만 실질적으로 사용되는 vector들은 high-dimensional vector이기 때문에 jacobian matrix는 매우매우 커져 연산량이 많아지게 되고 매우 sparse(matrix 값들이 대부분 0)해져 비효율적이게 되어 우리는 이러한 jacobian matrix를 대놓고 쓰지 않고 아래의 그림과 같은 implicit multiplication을 사용한다.
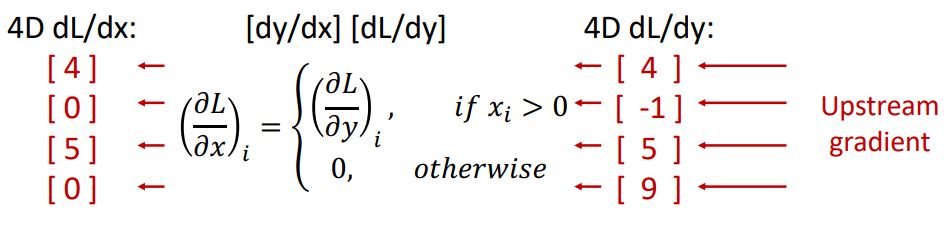
* 위의 implicit multiplication의 동작과정은 어렵지 않으니 한번 곱씹어보시기 바랍니다. 글로 설명하기 힘듭니다 ㅜㅜ
Backprop with matrices
우리가 흔히 봐왔던 Wx의 function으로 matrix valued backprop 과정을 살펴보자.
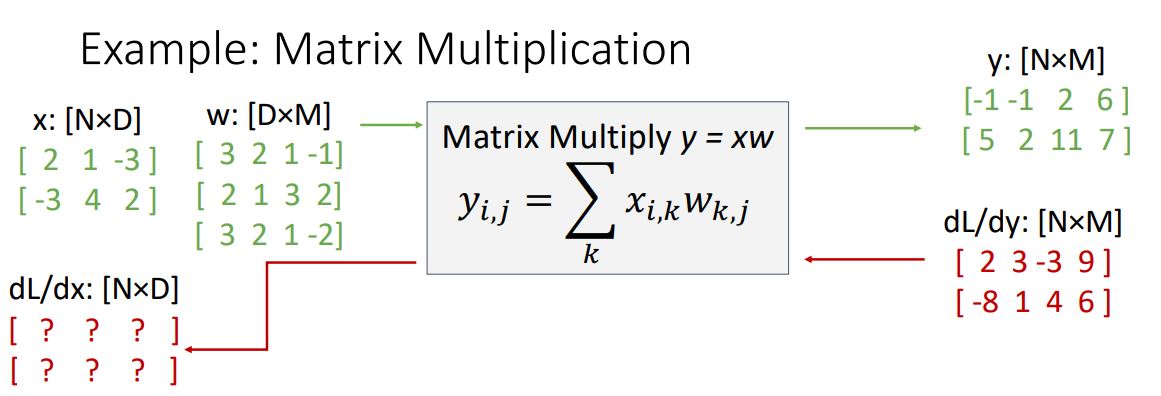
위 그림에서 주어진 x,w,y matrix들은 이전에 봤던 vector를 여러개 가지고있는 matrix라고 생각해보면 편하다.
일단 x는 N by D 형태의 matrix인데 이것은 D-dim row vector N개를 가지고있는 행렬의 형태 라고 생각해 볼 수 있다. 주어진 matrix로 보자면 3-dim vector 2개를 가진 matrix이다.
w matrix도 마찬가지이지만 matrix multiplication을 위해 tranpose시킨 형태로 x와 반대로 D-dim column vector M개를 가진 matrix이고. 주어진 matrix로 보았을 때는 3-dim column vector 4개를 가진 형태의 matrix이다.
마지막으로 y는 matrix multiplication 형태로 각 element가 x와 w의 element들로 이루어진 linear combination 형태이다. y11를 예로 들자면 , y11=x11∗w11+x12∗w21+x13∗w13 인 linear combination형태이다.
이제 backprop을 통해 x의 gradient를 구해야한다.
이 전에 보았듯이 downstream gradient는 local gradient와 upstream gradient를 곱하여 구해주었다.
다시 위 예시에서 local graient와 upstream gradient를 살펴보자.
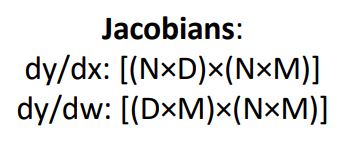
local gradient는 위와같은 형태의 매우 큰 jacobian matrix가 된다. 이전에 vector에대한 jacobian도 감당할 수 없는데 얘는 얼마나 큰지 상상도 하기 싫다.
그래서 우리는 jacobian matrix 전체를 multiplication해주어 downstream gradient를 구하는 것이 아니라 jacobian matrix를 implicitly하게 사용하여 element관점에서 하나하나 구해보려고 한다.
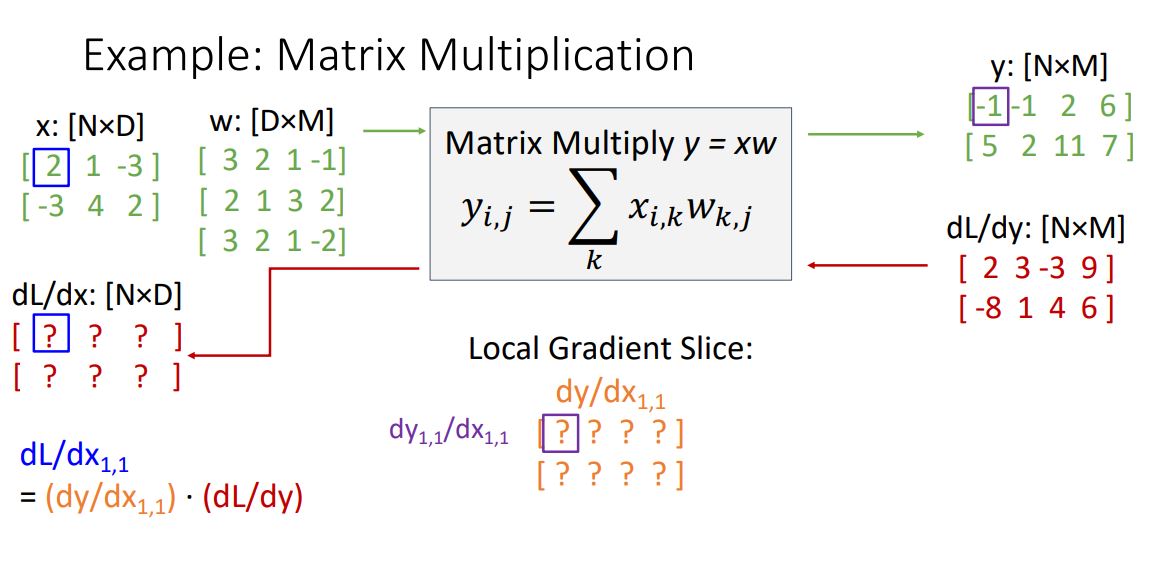
이런 dL/dx 에서 첫번째 element를 구해보자 (위 그림의 파란박스)
L을 x전체 가 아닌 하나의 element $x_{11}로 미분해 주면 당연하게도 dL/dx gradient의 첫번째 element가 된다. 이에 chain rule에 대입해보면 아래의 그림과 같은 수식이 나온다.

위 수식을 봤을때 빨간색에 해당하는 upstream gradient는 이미 주어졌고 주황색에 해당하는 local gradient를 구해야한다.

위와같은 local gradient를 구하기 위해선 또 각각의 element 관점에서 계산해 봐야 한다.
local gradient의 첫번째 element는 보라색 수식으로 나타낼 수 있다. 그니까 vector(y)를 scalar(x11)로 미분 했던 dy/dx11를 element하나 관점에서 vector y의 element y11 인 scalar를 x11인 scalar로 미분하였다고 보면 된다. 설명이 어려운데 아무튼 그렇다.
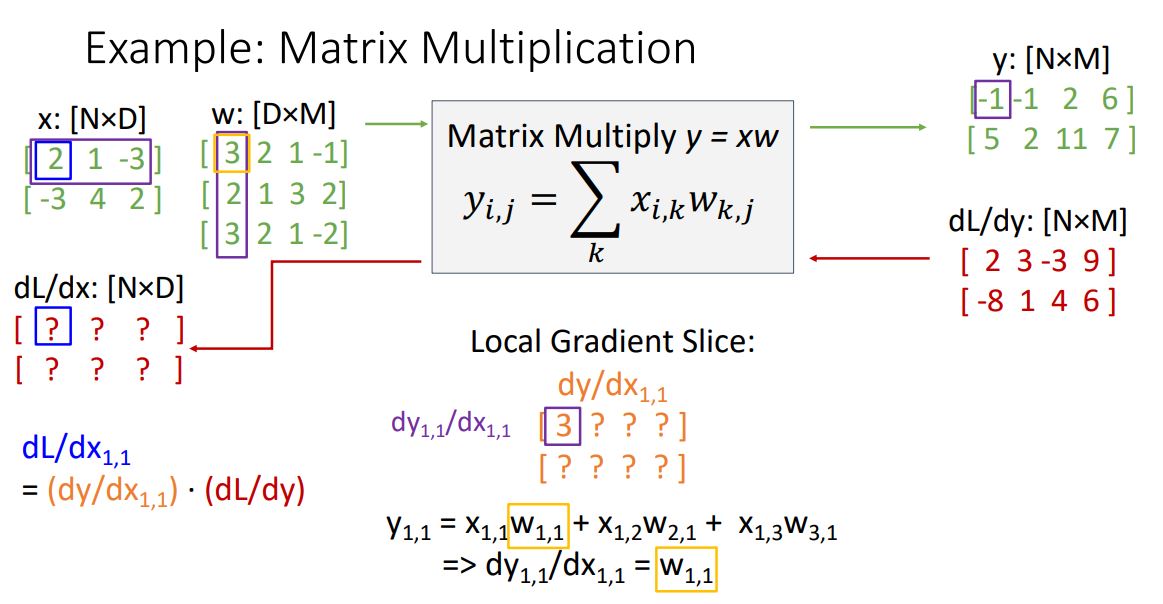
그래서 dy11/dx11을 구하기 위해 y11을 살펴보면 이 전에 말했던 linear combination이 된다. y11=x11∗w11+x12∗w21+x13∗w13
이 y11을 x11 로 편미분하면 위 linear combination에서 상수항은 다 날라가고 w11만 남게된다. 주어진 matrix로 계산하면 아래 그림과 같이 3이 된다.
위와같은 방식으로 local gradient의 element를 쭉쭉쭉 구하다보면 흥미로운 형태를 보게된다.
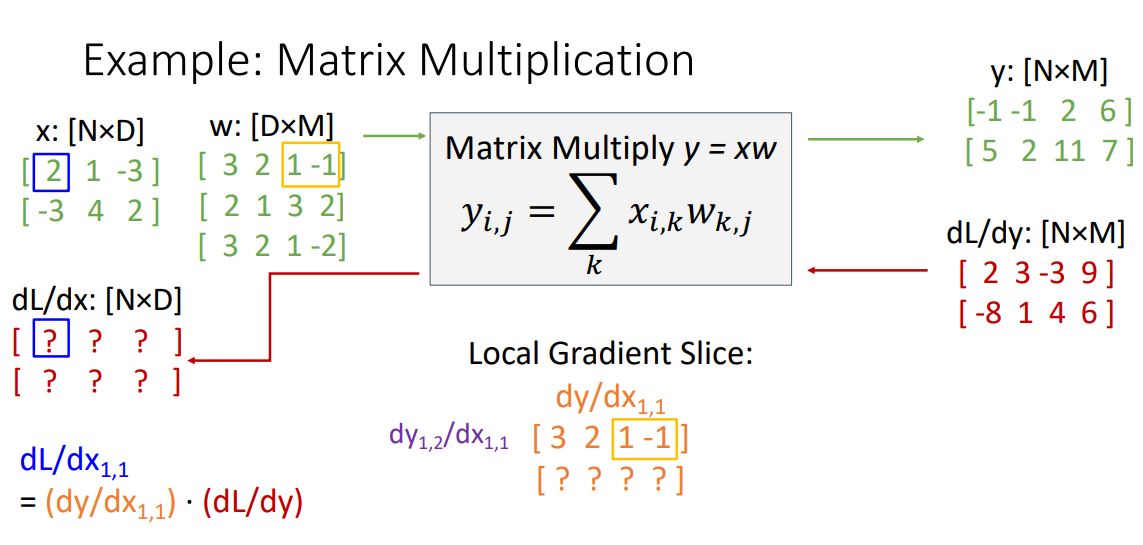
local gradient의 첫번째 row가 w의 첫번째 row가 된다는 것을 볼 수 있다.
그렇다면 local gradient의 두번째 row는 어떻게 될까?

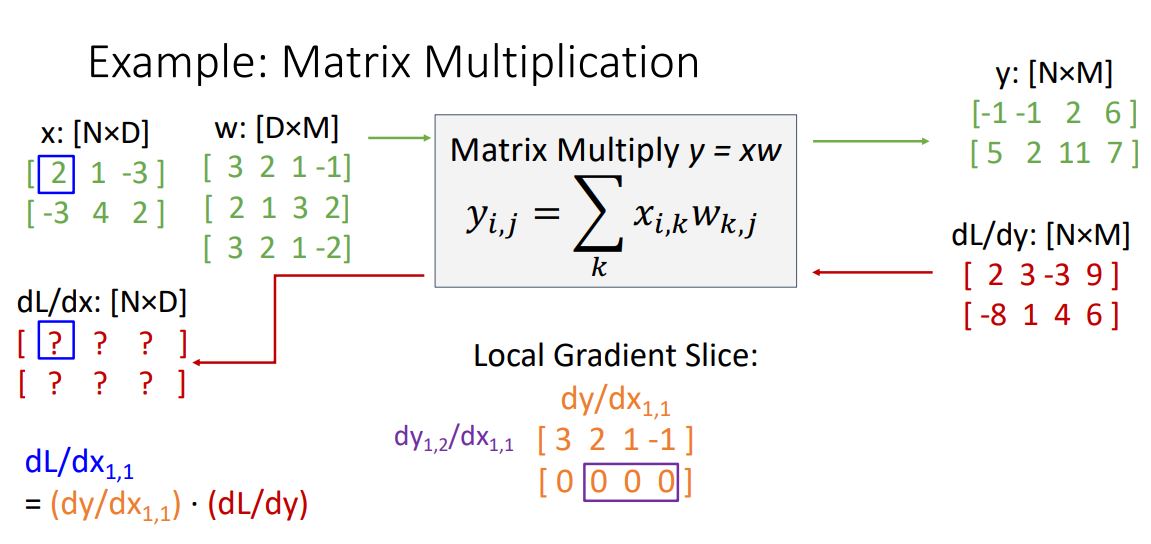
위 그림에서 보다시피 zero vector가 된다. 이는 조금만 생각해보면 당연한게 y12 를 x11로 편미분 한 것이니 y12의 linear combination에서 x11은 multiplication과정에서 관여되지 않았기에 x11항이 없게되고 편미분하면 전부 상수처리 되어 0이 된다.
이렇게 구한 local gradient slice와 upstream gradient를 곱해주면 dL/dx gradient의 element 하나를 구하게 된다.
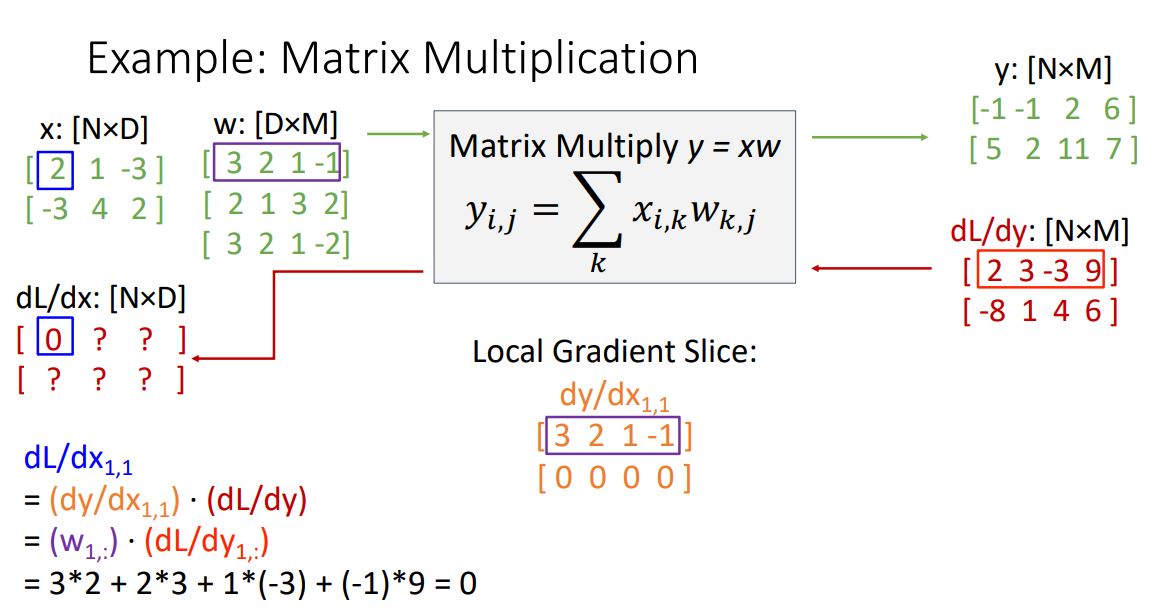
사실 local gradient와 upstream gradient의 matrix multiplication을 하기위해선 아래 그림과 같이 두 matrix의 순서를 바꾸고 upsteream gradient를 tranpose시켜줘야 한다.
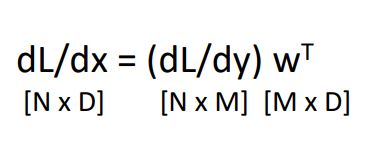
이러한 표현은 위 backprop pattens에서 mul node의 pattern이 여전히 적용되어 보인다.
* 위에서 local gradient를 dy/dx11 가 아닌 W로 나타낸 것은 zero vector부분은 어짜피 연산 하나마나이기 때문이다.
최종 형태는 다음과 같다.

Outro...
- 이번 backpropagation내용을 여러 예시를 통해 살펴보았다. 머리속으로는 이해하고있었지만 말로, 글로 풀어내기가 너무 힘들었고 그래서 글도 엄청 지저분해졌다.
