Linear Regression

---

일반적인 선형 모델은 아래의 식과 같이 input feature에 weight를 곱하여 더해준것에 bias라는 상수를 더하여 prediction을 도출한다.

선형회귀 모델의 예측

$\widehat{y}=\theta_0+\theta_1 x_1+\theta_2 x_2 + \cdot\cdot\cdot + \theta_n x_n$

• $\widehat{y}$ : 예측값
• n : 특성의 수
• $x_i$ : i번째 feature value
• $\theta_j$ : j번째 모델 파라미터 (bias $\theta_0$와 weights $\theta$를 포함한 표현)

이 식은 아래의 수식처럼 벡터 형태로 간단하게 표현 할 수 있다.

$\widehat{y}=h_\theta(x) = \theta^T\cdot x$

• $\theta^T$는 column vector이다.
• x 는 $x_0$에서 $x_n$까지 담고있는 sample의 feature vector이다.
• $h_\theta$는 모델 파라미터 $\theta$를 사용한 가설 hypothesis 함수이다.
  
  

이제 이 모델을 훈련시킬 것이다. 모델을 훈련시킨다는 것은 모델이 훈련 세트에 가장 잘 맞도록 파라미터를 설정해야하는 것 이다. 이를 위해선 loss function을 이용하여 loss를 최소화하는 $\theta$를 찾아야 한다. 일반적으로 회귀 문제에 가장 널리 사용되는 MSE(Mean Square Error) 를 loss function으로 사용 할 것이다.
Training set X 에 대한 선형회귀가설 $h_\theta$ 의 MSE는 아래와같이 표현 된 다.

*RMSE(Root Mean Square Error) vs MAE(Mean Absolute Error)

RMSE와 MAE는 모두 predict vector와 target vector간 거리를 재는 방법이다.

벡터의 거리 혹은 크기(magnatitude)를 재는 방법을 norm 이라고 한다.

*Norm

L1 Norm(Manhattan Distance)

위 그림처럼 L1 Norm은 두 vector를 빼고 절대값을 취한 뒤 합한 것 이다. 간단한 예를 들면 x=(1,2), y=(-3,1)일때 d(x,y) = |1-(-3)| + |2-1| = 4+1 = 5 가 된다.

L2 Norm(Euclidean Distance)

위 그림처럼 L2 Norm은 두 vector의 각 element를 빼주고 제곱을 취한 후 합쳐 루트를 씌운 것이다. 이것도 간단하게 예를 들면 x=(1,2), y=(-3,1)일때 $\sqrt{8+1} = 3$ 이 된다.

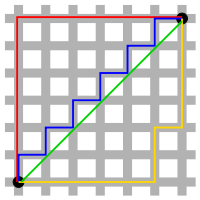
위 그림을 봤을때 두 개의 검은 점 (vector)를 잇는 여러 선 중 초록색 선은 L2 Norm (Euclidian distance)이고 나머지 선들은 모두 같은 L1 Norm (Manhattan Norm)이다.

LMSE는 L2 Norm (Euclidian Norm), MAE는 L2 Norm (Manhattan Norm)을 사용하여 계산되는 것 이다.

정규방정식 (Normal Equation)

---

loss function을 최소화하는 $\theta$값을 찾기위한 해석적인 방법으로 정규 방정식을 사용 할 수 있다.

정규방정식은 특정 linear regression 문제에서 $\theta$의 최적값을 구하는데 좋은 방법이다. gradient descent가 loss function의 최소값에 수렴하기 위하여 많은 반복을 수행하는 알고리즘인 반면에, 정규 방정식은 반복적으로 알고리즘을 돌릴 필요 없이 $\theta$를 직접 계산하여 최적값을 구하는 방식이다.

이전의 MSE 식에서 시그마를 없애고 행렬곱으로 표현하여 정규방정식을 이끌어낼 수 있다.

정규방정식 도출과정은 아래 블로그를 참고하면 좋다.

---

[머신러닝 reboot] 단순 선형 회귀 분석 - 정규방정식 도출하기 ]
출처: https://mazdah.tistory.com/831 [꿈을 위한 단상]

---

MSE 정규방정식

이제 위의 공식을 코드로 구현하여 값을 살펴보며 이해하자.

위의 공식을 테스트하기 위해 선형처럼 보이는 데이터를 생성해본다.

import numpy as np
import matplotlib.pyplot as plt

# 균일분포를 따르는 0-2 범위의 난수 생성 (*2를 해줌)
X = 2 * np.random.rand(100,1)
# np.random.randn(100,1) : 가우시안 노이즈를 위한 정규분포를 따르는 0-1 범위의 난수 생성
y = 4 + 3 * X + np.random.randn(100,1) 

plt.scatter(X, y) 
plt.show()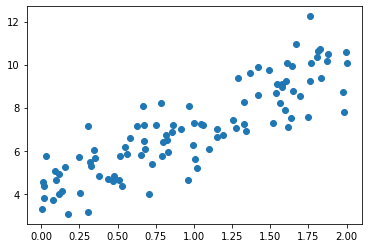

# X matrix 앞에 np.ones((100,1)) matrix를 붙여준다.
# np.concatenate((np.ones((100,1)), X), axis = 1) 와 동일
X_b = np.c_[np.ones((100,1)), X]

# np.linalg를 통해 정규방적식 계산
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)

print(theta_best)

[[4.11926714][2.9088166 ]]

# x = 0, 2 일때 θ^ 를 사용한 결과값을 이용하여 두 점을 이어 그래프 시각화
X_new = np.array([[0],[2]])
X_new_b = np.c_[np.ones((2,1)), X_new]

y_predict = X_new_b.dot(theta_best)
print('y_predict : \n', y_predict)

plt.plot(X_new, y_predict, 'r-')
plt.scatter(X,y)
plt.axis([0,2,0,15])
plt.show()

y_predict :
[[4.11926714][9.93690033]]

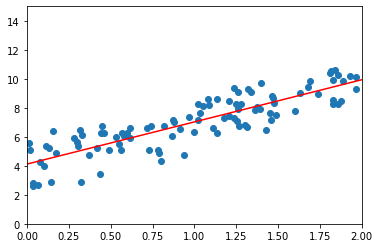
• 앞선 코드에서 정규방정식을 사용해 theta를 구할때 input set 인 cloumn vector X를 그대로 사용하는 것이 아니라 X 앞에 1들로 채워진 vector를 concatenate 시켜주는 이유가 궁금하여 아래 코드를 통해 살펴보았다.

# X matrix 에 상수항 column 이 들어가는 이유
# X_b 가인닌 X만을 이용하여 정규방정식을 통해 theta계산 후 y predict
theta2 = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)

y2_pred = X.dot(theta2)

plt.plot(X_new, y_predict, 'r-') 
plt.plot(X, y2_pred, 'b-') # X 만을 이용한 선형함수 시각화
plt.scatter(X,y)
plt.axis([0,2,0,15])
plt.show()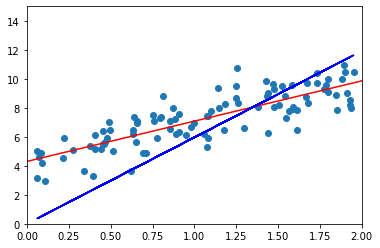

x cloumn vector만을 이용하여 theta를 구하고 그 theta를 적용한 선형 함수 시각화를 해보니 바로 정답을 알았다. 앞에선 흔히 말하는 bias를 theta($\theta_j$)와 분리하여 생각했으며 앞서 linear regression model을 정의 할 때 $\theta_0$ 가 bias인 것을 간과하였다.
바로 뒤에서 나오지만 이러한 내용이 Polynominal Regreesion의 핵심 개념이다.

• sklearn LinearRegression 라이브러리 사용

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X,y)
print(lin_reg.intercept_, lin_reg.coef_)

lin_reg.predict(X_new)

[4.11926714][2.9088166]]

array([[4.11926714],
[9.93690033]])

Polynominal Regression

---

가지고있는 데이터가 단순한 직선으로 표현이 안되는 복잡한 형태인 non-linear data도 linear model을 이용하여 학습 할 수 있다.

먼저 non-linear data로써 간단한 2차 방정식 형태를 띄는 data를 생성하여 본다.

m = 100 
# -3~3 범위를 가진 100개의 균일분포 data
X = 6 * np.random.rand(m, 1) - 3
Y = 0.5 * X**2 + X + 2 + np.random.randn(m,1)

plt.scatter(X,Y)
plt.show()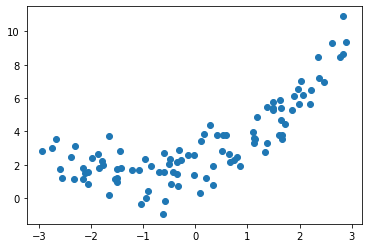

#linear regression에서 scalar column을 concatenate시켜준 것 처럼 
# 이번엔 X^2항 column까지 concatenate 시켜준다 

X_poly = np.array(X**2)
X_poly = np.c_[np.ones((100,1)), X, X_poly]

# np.linalg를 통해 정규방적식 계산
theta_best = np.linalg.inv(X_poly.T.dot(X_poly)).dot(X_poly.T).dot(Y)
theta_best
# theta_best[0] :theta_0 (bias)
# theta_best[0] :theta_1
# theta_best[0] :theta_2

array([[2.14583012],
[0.97614695],
[0.50492853]])

#predict 에 사용될 X data
X_new=np.linspace(-3, 3, 100).reshape(100, 1)
X_new_p = np.c_[np.ones((100,1)), X_new, X_new ** 2]
y_predict = X_new_p.dot(theta_best)

plt.plot(X_new, y_predict, 'r-')
plt.scatter(X,Y)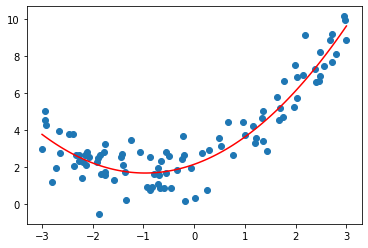

• sklearn LinearRegression 라이브러리 사용

from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)

lin_reg = LinearRegression()
lin_reg.fit(X_poly, Y)
lin_reg.intercept_, lin_reg.coef_

(array([2.14583012]), array([[0.97614695, 0.50492853]]))

Learning Curve

---

high-degre polynominal regression(고차다항회귀) model은 linear regression model보다 훨씬 더 training set에 잘 맞추려 학습 할 것이다.

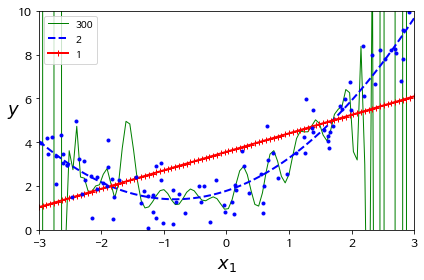
위의 그래프는 이전에 보았던 dataset에 300-degree polynominal regression model 과 linear regression model을 학습시킨 결과를 나타낸 것이다.
degree가 300인 model은 training data 에 overfitting 되어있다는 것을 볼 수 있고 linear model 은 underfitting 되어있다는 것을 볼 수있다. 2-degree regression model은 적절하게 일반화가 잘 되어있다고 볼 수 있다.

얼만큼의 degree를 가진 (얼만큼 복잡한) model을 사용해야하는지 알아야 한다.

model의 일반화 성능을 추정하기위한 방법으로 cross-validation 방법이 있다.

또 다른 학습 방법으로 learning curve를 살펴보는 방법이 있다.

learning curve의 그래프는 model의 성능을 train set과 validation set의 크기를 통해 나타낸다.

* 다음 코드를통해 주어진 training data에서 model의 learning curve를 살펴보자

from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

def plot_learning_curves(model, X, Y):
    X_train, X_val, y_train, y_val = train_test_split(X, Y, test_size=0.2, random_state=10)
    train_errors, val_errors = [], []
    for m in range(1, len(X_train)):
        model.fit(X_train[:m], y_train[:m])
        y_train_predict = model.predict(X_train[:m])
        y_val_predict = model.predict(X_val)
        train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
        val_errors.append(mean_squared_error(y_val, y_val_predict))

    plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train set")
    plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="valid set")
    plt.legend(loc="upper right", fontsize=11)
    plt.xlabel("training set size", fontsize=11)     
    plt.ylabel("RMSE", fontsize=11)   

위의 코드는 trining set과 valid set 크기를 증가시키면서 set크기마다 학습시킨 model을 mean square error 를 통해 성능을 계산하여 learning curve를 그려주는 함수를 정의한 것 이다.

* data set (X,Y)에는 위에서 사용하였던 2-degree polynominal에 가까운 data를 사용하였다.

linear model 의 learning curve를 살펴보자

lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, Y)
plt.axis([0, 80, 0, 3])
plt.show()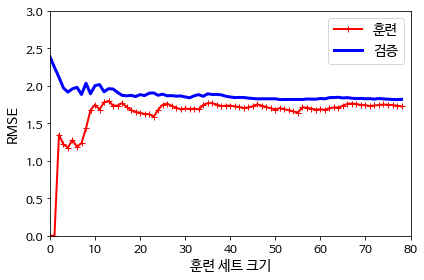

위 그림에서 train set에대한 그래프를 살펴보면 train set의 크기가 매우 작을땐 RMSE가 작아 model이 잘 작동한다. train set 크기가 커질수록 점점 오차가 증가하다가 일정 세트크기가 되면 곡선이 평탄해 지는 것을 볼 수 있다.
valid set 그래프를 보면 적은 수의 set에서는 일반화가 안되어 검증 오차가 크지만 set크기가 증가함에따라 오차가 작아지면서 일정 수 이상에서 train set의 오차와 비슷해지는 것을 볼 수 있다.

해당 그래프는 2-degree polynominal 에 가까운 data set에 linear model을 사용하였으므로 두 곡선이 수평한 구간을 만들면서 높은 오차를 보이는 것을 알 수 있다. 이러한 learning curve는 underfitting의 전형적인 예로 볼 수 있다.

* model이 underfitting 되어있다면 training set크기를 증가시켜도 효과가 없는 것을 알 수 있다.

이제 같은 data set을 사용해 10-degree model의 learning curve를 살펴보자

from sklearn.pipeline import Pipeline

polynomial_regression = Pipeline([
        ("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
        ("lin_reg", LinearRegression()),
    ])

plot_learning_curves(polynomial_regression, X, Y)
plt.axis([0, 80, 0, 3])
plt.show()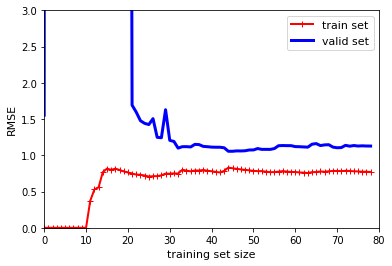          

위의 learning curve는 이전과 비슷해 보이자만 두가지 중요한 차이점이 있다.
하나는 training data의 오차가 linear model 보다 훨씬 낮다는 것이고. 다른 하나는 두 곡선 사이에 이전보다 큰 차이가 있다는 것으로 train set에서의 성능이 valid set에서의 성능보다 좋다는 것을 나타내고 이는 overfitting model의 특징으로 설명될 수 있다.

Overfit & Underfit / Bias & Variance

---

• bias : tain set의 error rate가 높아 model의 성능이 좋지 못할때 high bias를 갖는다고 한다. 이는 dataset에 따른 model의 평균 정확도를 측정하는 지표로도 쓰이며 underfitting과 관련이있다.
• variance : tain set의 error rate와 valid set의 error rate 차이가 클 때 high variance를 갖는다고 한다. 이는 model이 dataset에 대한 민감한 정도를 나타내기도 하며 overfitting과 관련이 있다.

high bias, high variance를 해결하는 방법들

• High bias? (train set performance)
  1. try bigger network!
  2. train longer!
  3. use advanced optimization algorithms!
  4. (or use other model)
• High variance? (valid set performance)
  1. get more data!
  2. regularization
  3. (or use other model)