- 그래프
- V : 노드의 집합
- E : 에지의 집합
- E는 VxV 의 부분집합(노드와 노드만을 이을 수 있다.
- 유향 그래프 VS 무향 그래프
- 에지의 방향이 있으면 유향 그래프, 없으면 무향 그래프(순서에 의미가 있다.)
- 무향 그래프는 양방향 유향 그래프로 생각할 수 있다.
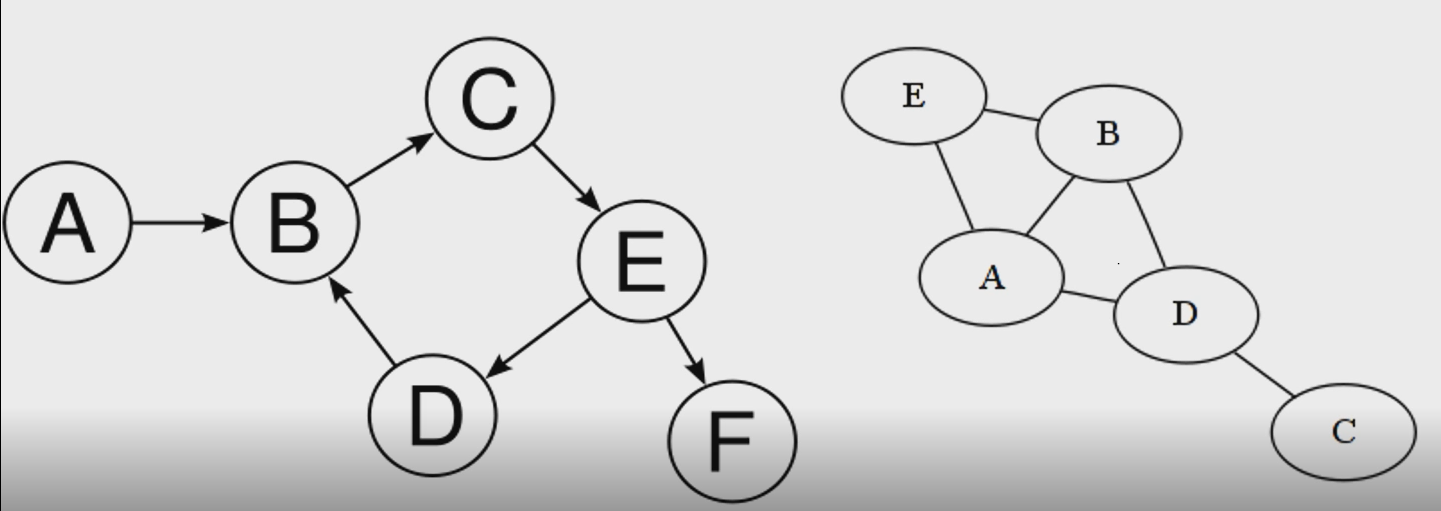
- 가중 그래프(weighted graph)
- G = (V,E,W)각 에지에 가중치가 매겨져 있다.
- 그래프의 표현
- 관계의 표현과 유사하다
- 행렬, 또는 리스트로 표현한다.
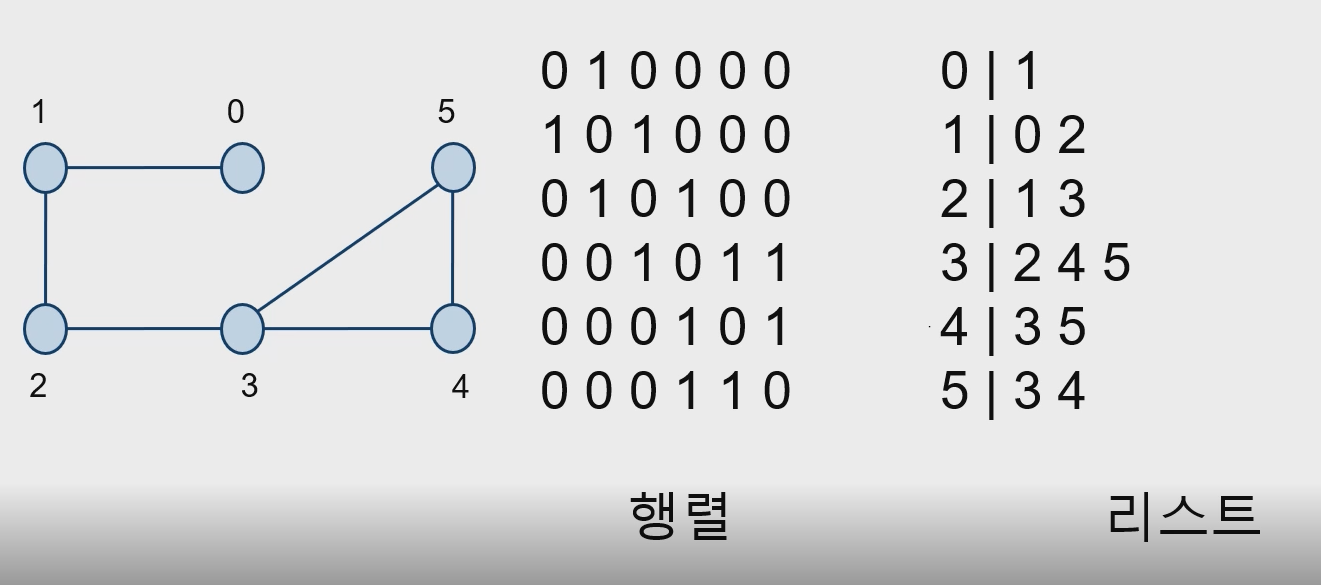
- ㄴ 행렬에서 1번과 0번이 연결되어 있으므로 1행 0열에 1값을 표시한다. 이어지지 않은 곳은 0을 표시한다.
- ㄴ 리스트 상에서는 각 노드와 연결된 노드들을 우측에 표시한다. 무향그래프는 유향 그래프와 다르게 리스트와 행렬에서 두번 표현된다.
- 가중 그래프의 표현
- 가중 그래프는 해당 에지의 가중치를 표현한다.
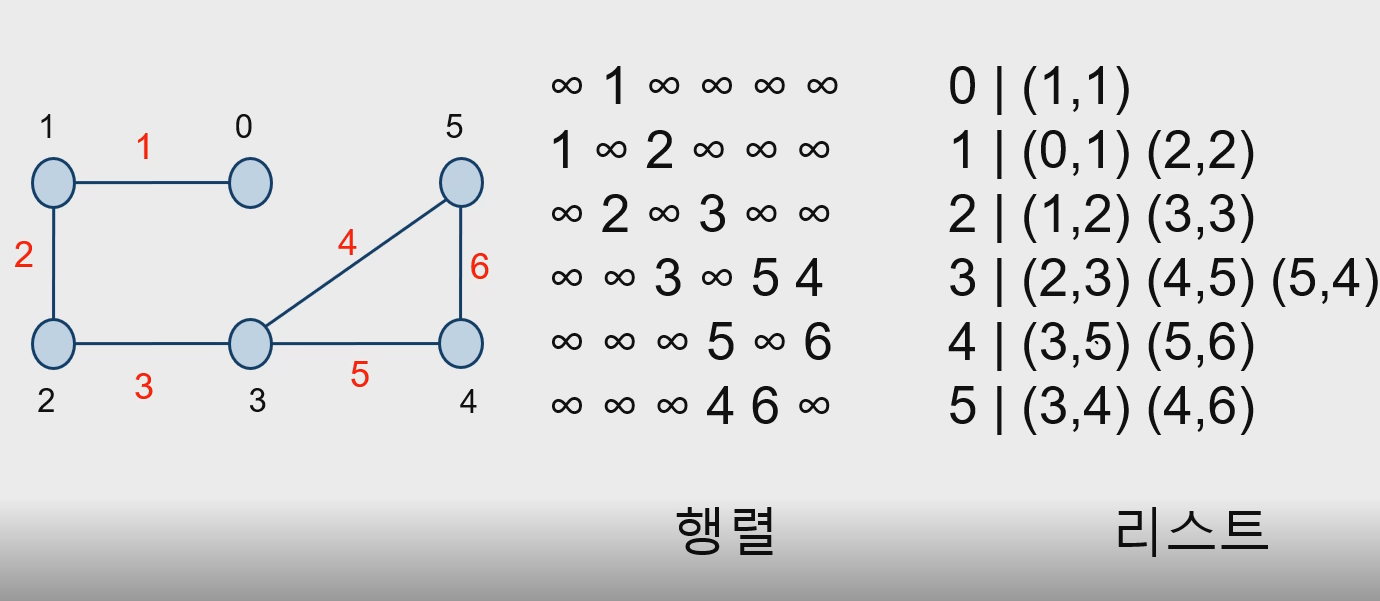
- ㄴ 행렬에서는 가는 경우가 없는 경우 무한대값을 표시한다.
- ㄴ 리스트에서는 해당하는 방향과, 가중치의 쌍으로 표현한다.
- 가중 그래프는 해당 에지의 가중치를 표현한다.
- 연결성
- 두 노드가 연결 -> 두 노드를 잇는 경로가 존재한다는 의미
- 그래프가 연결 -> 그래프의 어떤 두 노드를 골라도 연결
- 약한연결 : 한쪽으로만 갈 수 있다. / 강한연결 : 양쪽 모든 방향으로 갈 수 있다. 단 직접이 아니고 다른 노드를 거쳐서 가는 경우도 표현한다.
- 그래프의 탐색
- 그래프로 표현되는 문제를 풀기위한 기본적인 과정
-인접 행렬 / 리스트로 표현된 그래프를 원래 그래프로 복원하는 과정이다. - 크게 두가지의 방법
-깊이 우선 탐색(DFS) : 연결된 노드를 계속하여 탐색
-너비 우선 탐색(BFS) : 한 노드에서 연결된 노드들을 차례대로 탐색해 나감
- 깊이 우선 탐색
- 재귀, 스택 방법을 이용하여 구현할 수 있다.
- 한 노드를 탐색하여 최대 깊이까지 탐색 한다. 탐색할 시 이전에 방문한 곳은 체크하지 않는다. 이 후 다른 노드를 재귀적인 방법으로 동일하게 탐색한다.
- 너비 우선 탐색
- 시작부분부터 길이가 1인 곳을 모두 방문 한 후, 시작부분에서 거리가 2인 노드들을 모두 방문한다. 방문 과정에서 이미 방문한 곳은 체크하지 않는다. 같은 논리로 최대 거리만큼 탐색한 후 결과를 반환한다. 따라서 트리의 형태를 갖는다.
- 탐색 알고리즘의 시간/공간 복잡도
- 깊이 우선 탐색
-시간복잡도 : 모든 노드와 에지를 조사해야 하므로 O(V+E)
-공간 복잡도 : 모든 노드에 방문 여부를 체크해야 하므로 O(V) - 너비 우선 탐색
-시간 복잡도 : 모든 노드가 큐에 들어간 후 나와야 하고, 이는 에지를 따라 수행 되기 때문에 O(V+E)
-공간 복잡도 : 모든 노드에 방문 여부 및 큐에 포함 여부를 체크해야 하므로 O(V)
백엔드 & 전공 공부