- 분할상환 기법
- 알고리즘의 시간복잡도를 측정하는 방법
- 지금까지의 최악의 경우를 고려하고, 이때의 시간/공간 비용을 고려함
-어떤 연산은 다른 연산에 비해 시간이 많이 소요된다. - 어떻게 측정할 것인가
- 상한 : 최악의 경우시간 * 연산의 횟수
-필요한 연산들의 시간 총합을 잴 수 있다면 이것이 보다 정확한 척도
-평균적인 시간 복잡도와 다르다. 최악의 경우를 분석하는 것은 같고, 최악의 경우에 드는 시간을 보다 엄밀하게 재는 방법
- 예제 : 스택
- Push, pop을 지원하는 스택에
- Multipop : 스택에서 제일 위 k개의 원소를 리턴하고 스택에서 제거하는 기능을 추가한다.
- push(x), pop, Multipop(k)가 서로 섞여서 동작한다면 시간이 얼마나 걸릴 것인가?
- 스택분석 착한점
-가장 많이 걸리는 연산은 총 n개 있을때, 처음 n-1번 push 한다음 마지막 Multipop(n-1)을 하면 마지막 연산은 n-1시간이 걸린다.
-각 원소마다 스택 밖-> push-> 스택 안 -> pop/multipop-> 스택 밖의 주기를 따른다.
-그러므로, 원소 하나마다 최대 2번의 연산을 겪는다-> 2n번 이상 연산을 할 수 없다. - MultiPop 분석
-MultiPop(k)는 O(k) 시간에 동작한다.
-스택에서 꺼내려면 먼저 스택에 들어가야 한다.
-처음 빈 스택에서 동작한다면 다음 식이 성립한다.
-꺼낸 원소의 수<= 스택에 들어간 원소의 수
- 예제 : 동적 테이블 할당
- 프로그램에서 n칸의 메모리가 필요하다고 하자
- 보통 n이 얼마인지 미리 알기 쉽지 않다.
-미리 많이 잡았지만, 더 필요한다면 어떻게 할 것인가 - 전략
-처음 메모리를 1칸만 확보한다.
-만약 메모리가 더 필요하면, 지금 확보한 메모리 칸수 *2 만큼 메모리를 새로 잡은 후, 이전의 기록한 데이터를 복사한다.
-분명히 이외 같은 전략으로, 추가적인 일(데이터 복사)를 해야한다.
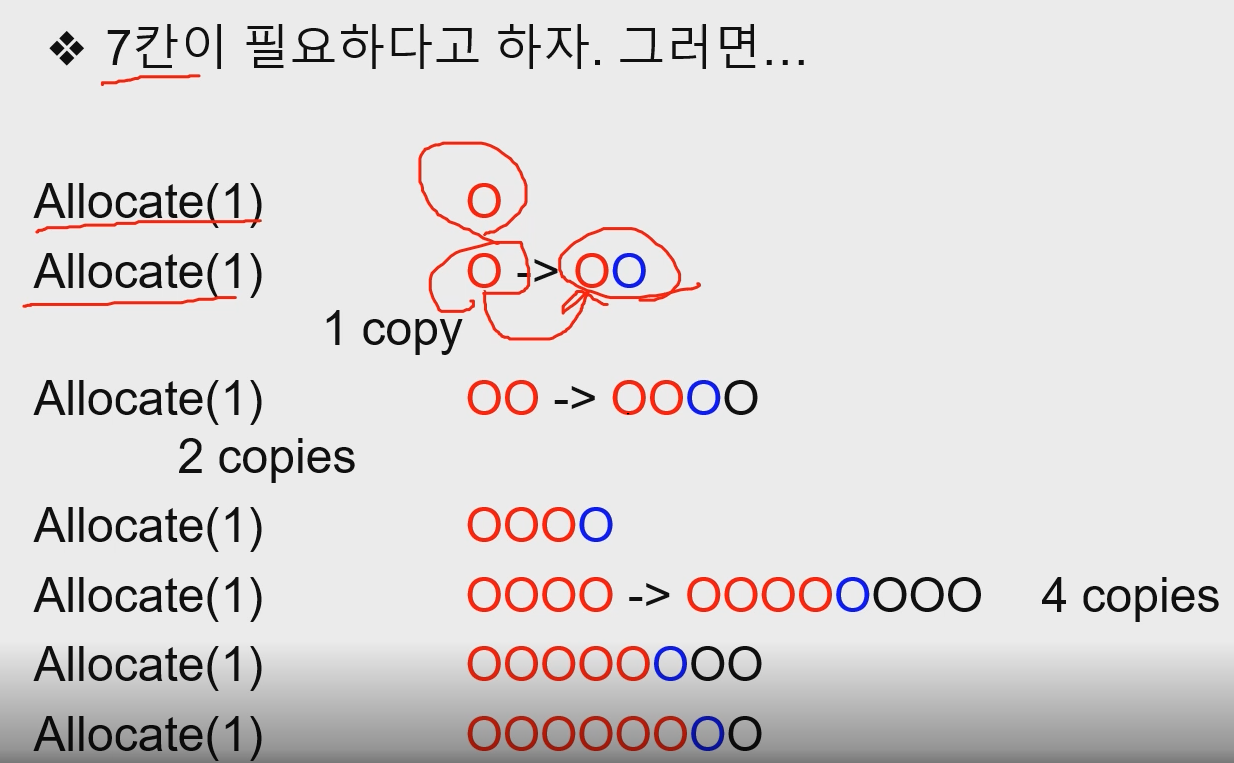
- 시간복잡도
-최악의 경우는 n=2^k 일 때이다.
-복사 횟수의 총 합은 2^k-1= n-1이다.
- 프로그램에서 n칸의 메모리가 필요하다고 하자
백엔드 & 전공 공부